Meep Reference
From AbInitio
| Revision as of 04:55, 7 November 2005 (edit) Stevenj (Talk | contribs) ← Previous diff |
Revision as of 05:20, 7 November 2005 (edit) Stevenj (Talk | contribs) Next diff → |
||
| Line 66: | Line 66: | ||
| ; <code>pi</code> [<code>number</code>] | ; <code>pi</code> [<code>number</code>] | ||
| : π (3.14159...). | : π (3.14159...). | ||
| + | |||
| + | == Classes == | ||
| + | |||
| + | Classes are complex datatypes with various "properties" which may have default values. Classes can be "subclasses" of other classes; subclasses inherit all the properties of their superclass, and can be used any place the superclass is expected. An object of a class is constructed with: | ||
| + | |||
| + | (make ''class'' (''prop1 val1'') (''prop2 val2'') ...) | ||
| + | |||
| + | See also the [[libctl manual]]. | ||
| + | |||
| + | Meep defines several types of classes, the most numerous of which are the various geometric object classes (which are the same as those used in [[MPB]]. You can also get a list of the available classes, along with their property types and default values, at runtime with the <code>(help)</code> command. | ||
| + | |||
| + | === lattice === | ||
| + | |||
| + | The lattice class is normally used only for the <code>geometry-lattice</code> variable, which sets the size of the computational cell. In [[MPB]], you can use this to specify a variety of affine lattice structures. In [[Meep]], only rectangular Cartesian computational cells are supported, so the only property of lattice that you should normally use is its <code>size</code>. | ||
| + | |||
| + | ; <code>lattice</code> | ||
| + | : Properties: | ||
| + | ;; <code>size</code> [<code>vector3</code>] | ||
| + | :: The size of the computational cell. Defaults to unit lengths. | ||
| + | If any dimension has the special size <code>no-size</code>, then the dimensionality of the problem is (essentially) reduced by one; strictly speaking, the dielectric function is taken to be uniform along that dimension. | ||
| + | |||
| + | Because Maxwell's equations are scale-invariant, you can use any units of distance you want to specify the cell size: nanometers, inches, parsecs, whatever. However, it is usually convenient to pick some characteristic lengthscale of your problem and set that length to 1. See also [[Meep Introduction#Units in Meep]]. | ||
| + | |||
| + | === material-type === | ||
| + | |||
| + | This class is used to specify the materials that geometric objects are made of. Currently, there are three subclasses, <code>dielectric</code>, <code>perfect-metal</code>, and <code>material-function</code>. | ||
| + | |||
| + | ; <code>dielectric</code> | ||
| + | : A uniform, isotropic, possibly nonlinear or dispersive, dielectric material; see also [[Dielectric materials in Meep]]. It has three properties: | ||
| + | ;; <code>epsilon</code> [<code>number</code>] | ||
| + | :: The dielectric constant (must be positive). No default value. You can also use <code>(index ''n'')</code> as a synonym for <code>(epsilon (* ''n n''))</code>. | ||
| + | ;; <code>chi2</code>[<code>number</code>] | ||
| + | :: The Kerr susceptibility <code>\chi^{(2)}</code>. | ||
| + | ;; polarizations [list of <code>polarizability</code> class] | ||
| + | :: List of dispersive polarizabilities (see below) added to the dielectric constant, in order to model material dispersion; defaults to none. | ||
| + | ; <code>perfect-metal</code> | ||
| + | : A perfectly conducting metal; this class has no properties and you normally just use the predefined <code>metal</code> object, above. (To model imperfect conductors, use a dispersive dielectric material.) | ||
| + | ; <code>material-function</code> | ||
| + | : This material type allows you to specify the material as an arbitrary function of position. It has one property: | ||
| + | ;; <code>material-func</code> [<code>function</code>] | ||
| + | :: A function of one argument, the position <code>vector3</code>, that returns the material at that point. Note that the function you supply can return ''any'' material; wild and crazy users could even return another <code>material-function</code> object (which would then have its function invoked in turn). | ||
| + | |||
| + | Dispersive dielectric materials, above, are specified via a list of objects of type <code>polarizability</code>, which is another class with four properties: | ||
| + | |||
| + | ; <code>polarizability</code> | ||
| + | : Specifies a single dispersive polarizability of damped harmonic form (see [[Dielectric materials in Meep#Material dispersion|Material dispersion]]), with the parameters: | ||
| + | ;; <code>omega</code> [<code>number</code>] | ||
| + | :: The resonance frequency <math>\omega_n</math>. | ||
| + | ;; <code>gamma</code> [<code>number</code>] | ||
| + | :: The resonance frequency <math>\gamma_n</math>. | ||
| + | ;; <code>sigma</code> [<code>number</code>] | ||
| + | :: The scale factor <math>\sigma_n</math>. | ||
| + | ;; <code>energy-saturation</code> [<code>number</code>] | ||
| + | :: See [[Saturable gain in Meep]]. | ||
| + | |||
| + | === geometric-object === | ||
| + | |||
| + | This class, and its descendants, are used to specify the solid geometric objects that form the dielectric structure being simulated. The base class is: | ||
| + | |||
| + | ; <code>geometric-object</code> | ||
| + | : Properties: | ||
| + | ;; <code>material</code> [<code>material-type</code> class] | ||
| + | :: The material that the object is made of (usually some sort of dielectric). No default value (must be specified). | ||
| + | ;; <code>center</code> [<code>vector3</code>] | ||
| + | :: Center point of the object. No default value. | ||
| + | |||
| + | One normally does not create objects of type <code>geometric-object</code> directly, however; instead, you use one of the following subclasses. Recall that subclasses inherit the properties of their superclass, so these subclasses automatically have the <code>material</code> and <code>center</code> properties (which must be specified, since they have no default values). | ||
| + | |||
| + | In a two-dimensional calculation, only the intersections of the objects with the x-y plane are considered. | ||
| + | |||
| + | ; <code>sphere</code> | ||
| + | : A sphere. Properties: | ||
| + | ;; <code>radius</code> [<code>number</code>] | ||
| + | :: Radius of the sphere. No default value. | ||
| + | ; <code>cylinder</code> | ||
| + | : A cylinder, with circular cross-section and finite height. Properties: | ||
| + | ;; <code>radius</code> [<code>number</code>] | ||
| + | :: Radius of the cylinder's cross-section. No default value. | ||
| + | ;; <code>height</code> [<code>number</code>] | ||
| + | :: Length of the cylinder along its axis. No default value. | ||
| + | ;; <code>axis</code> [<code>vector3</code>] | ||
| + | :: Direction of the cylinder's axis; the length of this vector is ignored. Defaults to point parallel to the <math>z</math> axis. | ||
| + | ; <code>cone</code> | ||
| + | : A cone, or possibly a truncated cone. This is actually a subclass of <code>cylinder</code>, and inherits all of the same properties, with one additional property. The radius of the base of the cone is given by the <code>radius</code> property inherited from <code>cylinder</code>, while the radius of the tip is given by the new property: | ||
| + | ;; <code>radius2</code> [<code>number</code>] | ||
| + | :: Radius of the tip of the cone (i.e. the end of the cone pointed to by the <code>axis</code> vector). Defaults to zero (a "sharp" cone). | ||
| + | ; <code>block</code> | ||
| + | : A parallelepiped (i.e., a brick, possibly with non-orthogonal axes). Properties: | ||
| + | ;; <code>size</code> [<code>vector3</code>] | ||
| + | :: The lengths of the block edges along each of its three axes. Not really a 3-vector, but it has three components, each of which should be nonzero. No default value. | ||
| + | ;; <code>e1</code>, <code>e2</code>, <code>e3</code> [<code>vector3</code>] | ||
| + | :: The directions of the axes of the block; the lengths of these vectors are ignored. Must be linearly independent. They default to the three lattice directions. | ||
| + | ; <code>ellipsoid</code> | ||
| + | : An ellipsoid. This is actually a subclass of <code>block</code>, and inherits all the same properties, but defines an ellipsoid inscribed inside the block. | ||
| + | |||
| + | Here are some examples of geometric objects created using the above classes, assuming <code>mat</code> is some material we have defined: | ||
| + | |||
| + | ; A cylinder of infinite radius and height 0.25 pointing along the x axis, | ||
| + | ; centered at the origin: | ||
| + | (make cylinder (center 0 0 0) (material mat) | ||
| + | (radius infinity) (height 0.25) (axis 1 0 0)) | ||
| + | |||
| + | ; An ellipsoid with its long axis pointing along (1,1,1), centered on | ||
| + | ; the origin (the other two axes are orthogonal and have equal | ||
| + | ; semi-axis lengths): | ||
| + | (make ellipsoid (center 0 0 0) (material mat) | ||
| + | (size 0.8 0.2 0.2) | ||
| + | (e1 1 1 1) | ||
| + | (e2 0 1 -1) | ||
| + | (e3 -2 1 1)) | ||
| + | |||
| + | ; A unit cube of material m with a spherical air hole of radius 0.2 at | ||
| + | ; its center, the whole thing centered at (1,2,3): | ||
| + | (set! geometry (list | ||
| + | (make block (center 1 2 3) (material mat) (size 1 1 1)) | ||
| + | (make sphere (center 1 2 3) (material air) (radius 0.2)))) | ||
Revision as of 05:20, 7 November 2005
| Meep |
| Download |
| Release notes |
| FAQ |
| Meep manual |
| Introduction |
| Installation |
| Tutorial |
| Reference |
| C++ Tutorial |
| C++ Reference |
| Acknowledgements |
| License and Copyright |
Here, we document the features exposed to the user by the Meep package. We do not document the Scheme language or the functions provided by libctl (see also the libctl User Reference section of the libctl manual).
This page is simply a compact listing of the functions exposed by the interface; for a gentler introduction, see the Meep tutorial. Also, we note that this page is not, and probably never will be, a complete listing of all functions. In particular, because of the SWIG wrappers, every function in the C++ interface is accessible from Scheme, but not all of these functions are documented or intended for end users.
Contents |
Input Variables
These are global variables that you can set to control various parameters of the Meep computation. In brackets after each variable is the type of value that it should hold. (The classes, complex datatypes like geometric-object, are described in a later subsection. The basic datatypes, like integer, boolean, cnumber, and vector3, are defined by libctl.)
-
geometry[list ofgeometric-objectclass] - Specifies the geometric objects making up the structure being simulated. When objects overlap, later objects in the list take precedence. Defaults to no objects (empty list).
-
sources[list ofsourceclass] - Specifies the current sources to be present in the simulation; defaults to none.
-
symmetries[list ofsymmetryclass] - Specifies the spatial (mirror/rotation) symmetries to exploit in the simulation (defaults to none). The symmetries must be obeyed by both the structure and by the sources. See also: Exploiting symmetry in Meep.
-
pml-layers[list ofpmlclass] - Specifies the absorbing PML boundary layers to use; defaults to none.
-
default-material[material-typeclass] - Holds the default material that is used for points not in any object of the geometry list. Defaults to
air(ε of 1). -
geometry-lattice[latticeclass] - Specifies the the size of the unit cell (which is centered on the origin of the coordinate system). If any dimension of the lattice
sizeis the special valueno-size, then the dimension of the lattice is reduced (i.e. it becomes two- or one-dimensional) by default. Defaults to a cubic cell of unit size. -
dimensions[integer] - Explicitly specifies the dimensionality of the simulation, if the value is less than 3. If the value is 3 (the default), then the dimensions are automatically reduced if possible when any of the
geometry-latticesizes areno-size. Ifdimensionsis the special value ofCYLINDRICAL, then cylindrical coordinates are used and the x and z dimensions are interpreted as r and z, respectively. -
m[number] - For
CYLINDRICALsimulations, specifies that the angular φ dependence of the fields is of the form eimφ (default ism=0). If the simulation cell includes the origin r = 0, thenmmust be an integer. -
resolution[numberorvector3] - Specifies the computational grid resolution, in pixels per distance unit. Defaults to
10. -
ensure-periodicity[boolean] -
k-point[falseorvector3] - If
false(the default), then the boundaries are perfect metallic (zero electric field). If a vector, then the boundaries are Bloch-periodic: the fields at one side are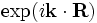 times the fields at the other side, separated by the lattice vector
times the fields at the other side, separated by the lattice vector 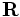 . The
. The k-pointvector is specified in Cartesian coordinates, in units of 2π/distance. (This is different from MPB, equivalent to taking MPB'sk-pointsthrough the functionreciprocal->cartesian.) -
ensure-periodicity[boolean] - If
true(the default), and if the boundary conditions are periodic (k-pointis notfalse), then the geometric objects are automatically repeated periodically according to the lattice vectors (the size of the computational cell). -
force-complex-fields?[boolean] - By default, Meep runs its simulations with purely real fields whenever possible. It uses complex fields (which require twice the memory and computation) if the
k-pointis non-zero or ifmis non-zero. However, by settingforce-complex-fields?totrue, Meep will always use complex fields. See also: Complex fields in Meep. -
filename-prefix[string] - A string prepended to all output filenames. Defaults to the name of the current ctl file, with ".ctl" replaced by "-" (e.g.
foo.ctluses a"foo-"prefix). -
Courant[number] - Specify the Courant factor S which relates the time step size to the spatial discretization
- cΔt = SΔx. Default is
0.5. For numerical stability, the Courant factor must be at most Failed to parse (unknown error): 1/\sqrt{\textrm{# dimensions}}
, and in practice should be slightly smaller.
-
output-volume[meep::geometric_volume*] - Specifies the default region of space that is output by the HDF5 output functions (below); see also the
(volume ...)function to createmeep::geometric_volume*objects. The default is'()(null), which means that the whole computational cell is output. Normally, you should use the(in-volume ...)function to modify the output volume instead of settingoutput-volumedirectly. -
progress-interval[number] - Time interval (seconds) after which Meep prints a progress message; default is 4 seconds.
The require a bit more understanding of the inner workings of Meep to use (see also the SWIG wrappers).
-
structure[meep::structure*] - Pointer to the current structure being simulated; initialized by
(init-structure)which is called automatically by(init-fields)which is called automatically by any of the(run)functions. -
fields[meep::fields*] - Pointer to the current fields being simulated; initialized by
(init-fields)which is called automatically by any of the(run)functions. -
num-chunks[integer] - Minimum number of "chunks" (subarrays) to divide the structure/fields into (default 0); actual number is determined by number of processors, PML layers, etcetera. (Mainly useful for debugging.)
Predefined Variables
Variables predefined for your convenience and amusement.
-
air,vacuum[material-typeclass] - Two aliases for a predefined material type with a dielectric constant of 1.
-
metal[material-typeclass] - A predefined material type corresponding to a perfectly conducting metal (in which the electric field is zero).
-
nothing[material-typeclass] - A material that, effectively, punches a hole through other objects to the background (
default-materialorepsilon-input-file). -
infinity[number] - A big number (1.0e20) to use for "infinite" dimensions of objects.
-
pi[number] - π (3.14159...).
Classes
Classes are complex datatypes with various "properties" which may have default values. Classes can be "subclasses" of other classes; subclasses inherit all the properties of their superclass, and can be used any place the superclass is expected. An object of a class is constructed with:
(make class (prop1 val1) (prop2 val2) ...)
See also the libctl manual.
Meep defines several types of classes, the most numerous of which are the various geometric object classes (which are the same as those used in MPB. You can also get a list of the available classes, along with their property types and default values, at runtime with the (help) command.
lattice
The lattice class is normally used only for the geometry-lattice variable, which sets the size of the computational cell. In MPB, you can use this to specify a variety of affine lattice structures. In Meep, only rectangular Cartesian computational cells are supported, so the only property of lattice that you should normally use is its size.
-
lattice - Properties:
-
size[vector3] - The size of the computational cell. Defaults to unit lengths.
If any dimension has the special size no-size, then the dimensionality of the problem is (essentially) reduced by one; strictly speaking, the dielectric function is taken to be uniform along that dimension.
Because Maxwell's equations are scale-invariant, you can use any units of distance you want to specify the cell size: nanometers, inches, parsecs, whatever. However, it is usually convenient to pick some characteristic lengthscale of your problem and set that length to 1. See also Meep Introduction#Units in Meep.
material-type
This class is used to specify the materials that geometric objects are made of. Currently, there are three subclasses, dielectric, perfect-metal, and material-function.
-
dielectric - A uniform, isotropic, possibly nonlinear or dispersive, dielectric material; see also Dielectric materials in Meep. It has three properties:
-
epsilon[number] - The dielectric constant (must be positive). No default value. You can also use
(index n)as a synonym for(epsilon (* n n)). -
chi2[number] - The Kerr susceptibility
\chi^{(2)}. - polarizations [list of
polarizabilityclass] - List of dispersive polarizabilities (see below) added to the dielectric constant, in order to model material dispersion; defaults to none.
-
perfect-metal - A perfectly conducting metal; this class has no properties and you normally just use the predefined
metalobject, above. (To model imperfect conductors, use a dispersive dielectric material.) -
material-function - This material type allows you to specify the material as an arbitrary function of position. It has one property:
-
material-func[function] - A function of one argument, the position
vector3, that returns the material at that point. Note that the function you supply can return any material; wild and crazy users could even return anothermaterial-functionobject (which would then have its function invoked in turn).
Dispersive dielectric materials, above, are specified via a list of objects of type polarizability, which is another class with four properties:
-
polarizability - Specifies a single dispersive polarizability of damped harmonic form (see Material dispersion), with the parameters:
-
omega[number] - The resonance frequency ωn.
-
gamma[number] - The resonance frequency γn.
-
sigma[number] - The scale factor σn.
-
energy-saturation[number] - See Saturable gain in Meep.
geometric-object
This class, and its descendants, are used to specify the solid geometric objects that form the dielectric structure being simulated. The base class is:
-
geometric-object - Properties:
-
material[material-typeclass] - The material that the object is made of (usually some sort of dielectric). No default value (must be specified).
-
center[vector3] - Center point of the object. No default value.
One normally does not create objects of type geometric-object directly, however; instead, you use one of the following subclasses. Recall that subclasses inherit the properties of their superclass, so these subclasses automatically have the material and center properties (which must be specified, since they have no default values).
In a two-dimensional calculation, only the intersections of the objects with the x-y plane are considered.
-
sphere - A sphere. Properties:
-
radius[number] - Radius of the sphere. No default value.
-
cylinder - A cylinder, with circular cross-section and finite height. Properties:
-
radius[number] - Radius of the cylinder's cross-section. No default value.
-
height[number] - Length of the cylinder along its axis. No default value.
-
axis[vector3] - Direction of the cylinder's axis; the length of this vector is ignored. Defaults to point parallel to the z axis.
-
cone - A cone, or possibly a truncated cone. This is actually a subclass of
cylinder, and inherits all of the same properties, with one additional property. The radius of the base of the cone is given by theradiusproperty inherited fromcylinder, while the radius of the tip is given by the new property:
-
radius2[number] - Radius of the tip of the cone (i.e. the end of the cone pointed to by the
axisvector). Defaults to zero (a "sharp" cone).
-
block - A parallelepiped (i.e., a brick, possibly with non-orthogonal axes). Properties:
-
size[vector3] - The lengths of the block edges along each of its three axes. Not really a 3-vector, but it has three components, each of which should be nonzero. No default value.
-
e1,e2,e3[vector3] - The directions of the axes of the block; the lengths of these vectors are ignored. Must be linearly independent. They default to the three lattice directions.
-
ellipsoid - An ellipsoid. This is actually a subclass of
block, and inherits all the same properties, but defines an ellipsoid inscribed inside the block.
Here are some examples of geometric objects created using the above classes, assuming mat is some material we have defined:
; A cylinder of infinite radius and height 0.25 pointing along the x axis,
; centered at the origin:
(make cylinder (center 0 0 0) (material mat)
(radius infinity) (height 0.25) (axis 1 0 0))
; An ellipsoid with its long axis pointing along (1,1,1), centered on
; the origin (the other two axes are orthogonal and have equal
; semi-axis lengths):
(make ellipsoid (center 0 0 0) (material mat)
(size 0.8 0.2 0.2)
(e1 1 1 1)
(e2 0 1 -1)
(e3 -2 1 1))
; A unit cube of material m with a spherical air hole of radius 0.2 at
; its center, the whole thing centered at (1,2,3):
(set! geometry (list
(make block (center 1 2 3) (material mat) (size 1 1 1))
(make sphere (center 1 2 3) (material air) (radius 0.2))))

