Meep C-plus-plus Tutorial
From AbInitio
| Revision as of 17:55, 25 October 2005 (edit) Mihai (Talk | contribs) (→Computing the Quality Factor of a Resonator - some rewording) ← Previous diff |
Revision as of 17:56, 25 October 2005 (edit) Mihai (Talk | contribs) (→Computing the Quality Factor of a Resonator - typo) Next diff → |
||
| Line 67: | Line 67: | ||
| const int N = 10; | const int N = 10; | ||
| - | Meep supports perfectly matching layers (PML) and absorbing boundary conditions. The PML begins at the edge of the computational volume and works inwards. Hence, we specify the size of the computational cell as follows: | + | Meep supports perfectly matching layers (PML) as absorbing boundary conditions. The PML begins at the edge of the computational volume and works inwards. Hence, we specify the size of the computational cell as follows: |
| const double pml_thickness = 1.0; | const double pml_thickness = 1.0; | ||
Revision as of 17:56, 25 October 2005
| Meep |
| Download |
| Release notes |
| FAQ |
| Meep manual |
| Introduction |
| Installation |
| Tutorial |
| Reference |
| C++ Tutorial |
| C++ Reference |
| Acknowledgements |
| License and Copyright |
Instead of using the libctl/Scheme interface described in the Meep tutorial, one can also access Meep as a C++ library by writing a C++ program that links to it. The C++ interface provides the greatest level of flexibility in designing FDTD simulations.
(This is, in fact, the original way in which we used Meep, and the way in which all of the Meep test programs, in its tests/ directory, are written.)
We should also note that, while Meep is nominally in C++, it is perhaps better described as "C+". That is, most of the coding style is C-like with a few C++ features.
Overview
We begin with a very brief outline of a Meep C++ program, with minimal explanations, leaving more details for the examples below and the C++ reference page. Your C++ program should begin with:
#include <meep.hpp> using namespace meep;
to include the definitions of the Meep routines. Later, when you compile (see below), you must also link to the Meep libraries.
Your main program should then initialize Meep, and will generally then define a computational volume and the associated structure (describing the geometry and materials), initialize the fields, add sources, and then time-step. In short:
int main(int argc, char **argv) {
initialize mpi(argc, argc); // do this even for non-MPI Meep
double resolution = 20; // pixels per distance
volume v = vol2d(5,10, resolution); // 5x10 2d cell
structure s(v, eps, pml(1.0));
fields f(&s);
f.output_hdf5(Dielectric, v.surroundings());
double freq = 0.3, fwidth = 0.1;
gaussian_src_time src(freq, fwidth);
f.add_point_source(Ey, src, vec(1.1, 2.3));
while (f.time() < f.last_source_time()) {
f.step();
}
f.output_hdf5(Hz, v.surroundings());
return 0;
}
This example, doesn't do much — it just runs a Gaussian source and outputs the 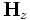 field at the end. The dielectric structure is determined by the user-defined function
field at the end. The dielectric structure is determined by the user-defined function eps, which has the form:
double eps(const vec &p) {
if (p.x() < 2 && p.y() < 3)
return 12.0;
return 1.0;
}
which returns the dielectric function 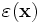 (here, just a 2×3 rectangle of ε=12 in the upper-left corner). Unlike in the libctl front-end, by default the origin 0 of the coordinate system is at the corner of the computational cell.
(here, just a 2×3 rectangle of ε=12 in the upper-left corner). Unlike in the libctl front-end, by default the origin 0 of the coordinate system is at the corner of the computational cell.
Now that you have the basic flavor, we can proceed to some more specific examples.
Computing the Quality Factor of a Resonator
In this first tutorial, we will write the script to compute the quality factor of a 1D Fabry-Perot cavity. For a 1D system, Meep considers a computational cell along the z coordinate. The control file will be a C++ file (having extension *.cpp). In order to use all the classes and subroutines available in Meep, the first two lines of any control file must be the following:
#include <meep.hpp> using namespace meep;
The particular Fabry-Perot cavity we will investigate consists of an air region bounded by two distributed Bragg reflectors (quarter-wave stack) of epsilon 12 and 1. We choose the size of the defect to be twice as large as the air thickness in the quarter-wave stack, so that a defect mode is found near midgap. This structure will include N = 10 periods in the Bragg reflector on either side of the defect. The parameters are set up as follows:
const double eps1 = 12.0; const double eps2 = 1.0; const double grating_periodicity = 1.0; const double d1 = sqrt(eps2) / (sqrt(eps1)+sqrt(eps2)); const double d2 = sqrt(eps1) / (sqrt(eps1)+sqrt(eps2)); const double half_cavity_width = d2; const int N = 10;
Meep supports perfectly matching layers (PML) as absorbing boundary conditions. The PML begins at the edge of the computational volume and works inwards. Hence, we specify the size of the computational cell as follows:
const double pml_thickness = 1.0; const double z_center = half_cavity_width + N*grating_periodicity + pml_thickness;
To specify a dielectric structure in Meep, we define a function that takes as input one parameter, a position vector, and returns the value of the dielectric at that position.
double eps(const vec &p) {
vec r = p - vec(z_center);
if (abs(r.z()) < half_cavity_width)
return 1.0;
else {
double dz = abs(r.z()) - half_cavity_width;
while (dz > grating_periodicity)
dz -= grating_periodicity;
return (dz < d1) ? eps1 : eps2;
}
}
We are now ready to set up the computational area, excite the sources, time step the fields, and compute the resulting quality factor. Here we set up the main part of the control file incorporating some of Meep's classes and sub routines. We will excite the mode at the midgap of the bandgap, which we expect to have the largest quality factor since it will have the largest exponential decay.
int main(int argc, char **argv){
initialize mpi(argc,argv);
const double amicron = 10.0;
const volume vol = vol1d(2*z_center,amicron);
structure s(vol,eps,pml(pml_thickness));
fields f(&s);
The sources in Meep are excitations of the polarization vector in 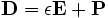 . The polarization can be any one of the six cartesian or cylindrical fields. There are a variety of sources including dipoles, gaussian pulses and a continuous wave source. For now, we use a gaussian source centered at the midgap frequency with a narrow width, along with the start time and end time of the source.
. The polarization can be any one of the six cartesian or cylindrical fields. There are a variety of sources including dipoles, gaussian pulses and a continuous wave source. For now, we use a gaussian source centered at the midgap frequency with a narrow width, along with the start time and end time of the source.
const double w_midgap = (sqrt(eps1)+sqrt(eps2))/(4*sqrt(eps1)*sqrt(eps2)); gaussian_src_time src(w_midgap, 1.0, 0.0, 5.0); f.add_point_source(Ex, src, vol.center());
Here we make use of the built in function, vol.center(), that automatically computes the geometric center of the of the computational volume. To see what the unit cell of the dielectric function looks, output has an HDF5 file, we invoke the built in command:
f.output_hdf5(Dielectric, v.surroundings())
This versatile command can be used to visualize all of the field components, field energy when called at a particular time step. The resulting output file will be 'eps-000000.00.h5' and to view it, we first need to convert it to the portable network graphics (PNG) format with the h5topng tool. We are now ready to begin the time stepping of the fields, and do so in a simple loop:
while (f.time() < f.last_source_time()) f.step();
To calculate the quality factor, we need to monitor a field beyond the time at which our point source has been turned off. We can do this in Meep by establishing an array where all fields at a particular point can be monitored. We set up the area as well as the output arrays we will need later as such:
int ttot = int(100/f.dt)+1; complex<double> *p = new complex<double>[ttot]; complex<double> *amps = new complex<double>[ttot]; double *freq_re = new double[ttot]; double *freq_im = new double[ttot];
ttot represents the total number of timesteps for which we will monitor the field component at. Now we are ready to time step and collect the field information:
int i=0;
while (f.time() < f.last_source_time() + 100) {
f.step();
p[i++] = f.get_field(Ex,vol.center());
}
The get_field function does exactly that, obtains the value of the field at a given position within the computational cell using linear interpolation where necessary. Now we have all the information we need and must obtain the frequencies of the modes which we do by invoking a special tool for harmonic inversation, harminv, to extract the real and imaginary frequencies:
int num = do_harminv(p, ttot, f.dt, 0.8*w_midgap, 1.2*w_midgap, 5, amps, freq_re, freq_im);
The integer returned by harminv is the number of mode frequencies obtained from the input data p. The particular call to harminv included passing the array values by value and telling harminv to look for frequencies within 20% of the mid gap frequency up to a maximum of 5 bands. At this point, the necessary information to compute the quality has been stored in the freq_re and freq_im arrays and we compute the quality factor using the formula, Q=2*\oemga_real/-omega_imag. All that is left to do, is to print these results with the quality factor:
master_printf("frequency,amplitude,quality factor\n");
for (int i=0; i<num; ++i)
master_printf("%0.6g%+0.6gi,%0.5g%+0.5gi,%g\n",freq_re[i],freq_im[i],real(amps[i]),imag(amps[i]),-2*freq_re[i]/freq_im[i]);
return 0;
}
That's it, we are done. The output for this program is -225210, which suggests that the quality factor is a very large number since machine error has resulted in a negative value. The large quality factor which is to be expected since our system includes a relatively high number of bragg reflectors (N=10) in each direction and we are exciting the mode at mid gap.

