Casimir calculations in Meep
From AbInitio
(diff) ←Older revision | Current revision | Newer revision→ (diff)
| Meep |
| Download |
| Release notes |
| FAQ |
| Meep manual |
| Introduction |
| Installation |
| Tutorial |
| Reference |
| C++ Tutorial |
| C++ Reference |
| Acknowledgements |
| License and Copyright |
Contents |
Casimir calculations in Meep
It is possible to use the Meep time-domain simulation code in order to calculate Casimir forces (and related quantities), a quantum-mechanical force that can arise even between neutral bodies due to quantum vacuum fluctuations in the electromagnetic field, or equivalently as a result of geometry dependence in the quantum vacuum energy.
Calculating Casimir forces in a classical time-domain Maxwell simulation like Meep is possible because of a new algorithm described in:
- Alejandro W. Rodriguez, Alexander P. McCauley, John D. Joannopoulos, and Steven G. Johnson, "Casimir forces in the time domain: I. Theory," arXiv preprint archive article arXiv:0904.0267 (April 2009).
- Alexander P. McCauley, Alejandro W. Rodriguez, John D. Joannopoulos, and Steven G. Johnson, "Casimir forces in the time domain: II. Applications," arXiv preprint archive article arXiv:0906.5170 (June 2009).
This page will provide some tutorial examples showing how these calculations are performed for simple geometries.
Introduction
In this section, we introduce the equations and basic considerations involved in computing the force using the method presented in Rodriguez et. al. (arXiv:0904.0267). Note that we keep the details of the derivation to a minimum and instead focus on the calculational aspects of the resulting algorithm.
The basic steps involved in computing the Casimir force are:
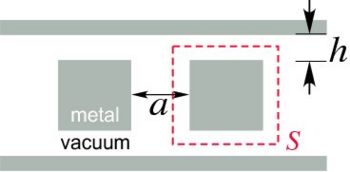
1. Surround the object for which the force is to be computed with a simple, closed surface S. It is often convenient to make S a rectangle in two dimensions and a rectangular prism in three dimensions.
2. Add a uniform, frequency-independent conductivity σ to the dielectric response of every object (which is easily done Meep). The purpose of this is to rapidly reduces the time required for the simulations below.
3. Measure the electric E and magnetic H fields on S in response to a set of different current distributions on S (more on the specific form of these currents later).
4. Integrate these fields over the enclosing surface S at each time step, and then integrate this result, multiplied by a known function g( − t), over time t.
The Casimir force is given by an expression of the form:
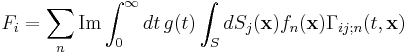
where Γij;n are the fields in response to sources related to the functions fn (discussed in detail later), S is an arbitrary closed surface enclosing the object for which we want to compute the Casimir force, g(t) is a known function, and the index n ranges over all of the integers.
<ref>Note that the precise implementation of step (3) will greatly affect the efficiency of the method. For example, computing the fields due to each source at each point on the surface separately requires a separate Meep calculation for each source (and polarization). As described in <ref name="Rodriguez"/>, and further below, it is possible to modify these steps in order to optimize the calculation of the stress tensor over the spatial surface. For the purpose of this introduction, however, we do not require specific details on how we handle the spatial integration.</ref>
Example: two-dimensional blocks
In this section we calculate the Casimir force in the two-dimensional double-block configuration (Rodriguez et. al, Physical Review Letters, vol 99, p 080401 2007) shown below:
The dashed red lines indicate the surface S. This system consists of two metal  squares in between metallic sidewalls. As described in Part II, the first step is to add a uniform, frequency-independent D-conductivity σ to all the dielectrics (in this case metal and vacuum):
squares in between metallic sidewalls. As described in Part II, the first step is to add a uniform, frequency-independent D-conductivity σ to all the dielectrics (in this case metal and vacuum):
(define-param Sigma 1) (define my-metal (make material (epsilon -1e20) (D-conductivity Sigma))) (define my-air (make material (epsilon -1e20) (D-conductivity Sigma))) (set! default-material my-air)
We then add in the double blocks:
(set! geometry
(list (make block (center a 0) (size a a infinity) (material my-metal))
(make block (center (- a) 0) (size a a infinity) (material my-metal))))
As discussed in Part I, the optimal value of σ depends on the system under consideration. In our case, σ = 1 appears to be optimal or near optimal.
In the ideal system the empty space extends to infinity in both the left and right directions. For a finite computational cell, we define a horizontal buffer region xbuffer and impose periodic boundary conditions in x and metallic boundary conditions in y:
(set! geometry-lattice (make lattice (size (+ (* 3 a) (* 2 xbuffer)) (+ a (* 2 h)) no-size)))
When imposing the boundary conditions, it is important to first initialize the fields in Meep:
(init-fields) (meep-fields-use-bloch X 0)
Note that this is different from (set! k-point (vector3 0)) as this will assign periodic boundary conditions to both x and y.
Defining the sources
We then define the surface S through lists containing the centers and sizes of each side of S:
(define block-cen (vector3 a 0 0)) (define xshift (vector3 (/ L 2) 0 )) (define yshift (vector3 0 (/ L 2)))
(define face-centers
(list (vector3- block-cen xshift) (vector3+ block-cen xshift)
(vector3- block-cen yshift) (vector3+ block-cen yshift)))
(define face-sizes
(list (vector3 0 L) (vector3 0 L) (vector3 L 0) (vector3 L 0)))
This contains all the information about S and can be used for many two-dimensional Casimir force calculations.
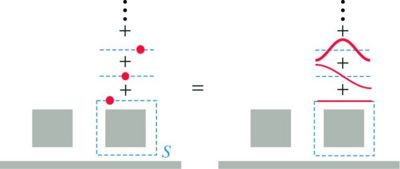
As described in Part II, the next step is to pick a basis of functions {fn} on S, indexed by n, such that these form a complete and orthonormal basis for all real-valued functions on S. Since S consists of four distinct line segments, we take a real cosine basis:
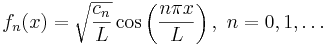
where cn = 1 if n = 0 and cn = 2 otherwise, L is the side length (if each side has a different length, then the functions fn(x) will differ for each side). An illustration of these functions for the system under consideration is shown below:
These functions fn(x) are easily defined in the ctl file:
(define (dct X n source-size)
(let*
((X-start (vector3+ X (vector3-scape 0.5 face-size))))
(x (vector3-x X-start))
(y (vector3-y X-start))
(kx (/ (* n pi) L))
(ky (/ (* n pi) L)))
(* (sqrt (/ (if (= n 0) 1 2) L)) (cos (* kx x)) (cos (* ky y))))
The reason for the shift from X to X-start is that the origin of the dct functions is the endpoint of the line segment, while the origin for a function (amp-func ...) is taken to be the center of the surface. Also, we are allowed to insert both (cos (* kx x)) and (cos (* ky y)), even though the face is actually one-dimensional. This is because, if the surface has zero size in one direction, that coordinate will always be zero (since the coordinates are relative to the center of the face), so the (cos ...) term in that direction will always be 1. Writing things this way merely simplifies the Scheme code.
A simulation is run for each n, each side of S, indexed by the integer side, and each source polarization. The source itself has the form:
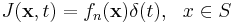
This is defined using the custom-src function:
(change-sources!
(list (make source
(src (make custom-src
(src-func (lambda (t) (if (= t (* 1.5 dt)) (/ 1 dt) 0)
(is-integrated? false) (start-time (- infinity)) (end-time 1)))
(center (list-ref face-centers side)) (size (list-ref face-sizes side))
(component current-pol) (amplitude 1)
(amp-func (lambda (X) (dct X n (list-ref face-sizes side))))))
where dt is the unit of time-stepping given by (meep-fields-dt-get fields).
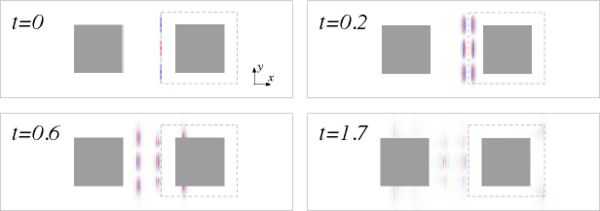
To illustrate the field profiles, below we show four snapshots at different times for what we term 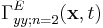 , the y-component of the electric field response to a y-polarized current source with spatial dependence f2(x)
, the y-component of the electric field response to a y-polarized current source with spatial dependence f2(x)
At each time-step, the fields are integrated over S, weighted by both fn(x) and g(t), yielding a differential increment in the force as a function of time:
![dF_{n} = \mathrm{Im}[g(t)] \int_S dS_j(\textbf{x}) f_n(\textbf{x}) \Gamma_{ij;n}(t,\textbf{x})](/wiki/images/math/a/4/b/a4bc1a92d75e083b25c5251163c7d0a6.png)
Computation of g(t)
As discussed in Part I, the function g(t) is directly computed as the Fourier transform of a function of real frequency ξ, g(ξ). This function is given by:
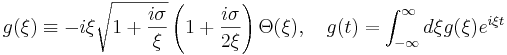
This Fourier transform can be computed numerically. However, as discussed in Part II, g(ξ) diverges in both the low-ξ and high-ξ limits, making numerical computation of the transform cumbersome. A method around this issue (discussed in the appendix of Part II) is to subtract off these asymptotic terms and evaluate their Fourier transforms analytically. The remaining function is bounded for all frequency and is easily handled numerically.
A Fourier transform is still clumsy to implement directly through the Scheme front-end. This is why, in the newest release of Meep, we have included a function (make-casimir-g ...) which will return a list whose values are g(t) where t < math > isgiveninincrementsofthetime − domainsimulation < math > dt:
(define gt (make-casimir-g T dt Sigma [eps-omega] [Tfft]))
Here T is the total simulation time, and the optional argument eps-omega accounts for dispersive materials (the influence of dispersion is discussed in Part I) and Tfft controls the frequency resolution of the Fourier transform (dξ˜1 / TFFT). By default, eps-omega is NULL and Tfft equals 10T.
Integration of the fields
As with the construction of g(t), the integration of the fields along S, weighted by the function fn(x), can be done in any version of meep through the Scheme interface. However, in this form, every pixel communicates through the Scheme interpreter at every timestep. This significantly slows down computation time; in fact, in two dimensions it dominates the actual time-stepping for resolutions below 400!
To circumvent this, the newest version of meep also has a built-in field-integration routine, (meep-fields-casimir-stress-dct-integral ...), which will automatically integrate the field response Γij;n along a specified face of S:
(define Gamma-integral-X
(meep-fields-casimir-stress-dct-integral fields X current-dir n n 0 E-stuff current-face))
The value of the force in direction x is then updated:
(set! Force-x (+ Force-x (* (imag-part (list-ref gt current-step)) Gamma-integral-X dt)))
We compress this into one function, to be called at every time-step:
(define (integrate-function)
(set! Gamma-integral-X
(meep-fields-casimir-stress-dct-integral fields X current-dir n n 0 E-stuff current-face))
(set! Force-x
(+ Force-x (* (imag-part (list-ref gt current-step)) Gamma-integral-X dt))))
(run-until T integrate-function)
The appropriate run time T depends upon the system under consideration. The the example of the double blocks, we find that by T = 40 the force has converged to within 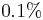 of its final value. Using the optimizations discussed above, it takes roughly 20 seconds to run simulation at resolution 40 for each value of n (that is, including all sides of S and all field polarizations). Typically, only
of its final value. Using the optimizations discussed above, it takes roughly 20 seconds to run simulation at resolution 40 for each value of n (that is, including all sides of S and all field polarizations). Typically, only 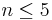 are needed to get the force to high precision, so the Casimir force for this system can be determined in under two minutes on a single processor.
are needed to get the force to high precision, so the Casimir force for this system can be determined in under two minutes on a single processor.
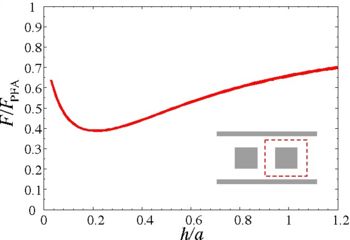
The result, when sampled over many values of h, is a force curve that varies non monotonically in h:
Example: cylindrical symmetry
[coming soon]
Example: three-dimensional computations
[coming soon]