Casimir calculations in Meep

It is possible to use the Meep time-domain simulation code in order to calculate Casimir forces (and related quantities), a quantum-mechanical force that can arise even between neutral bodies due to quantum vacuum fluctuations in the electromagnetic field, or equivalently as a result of geometry dependence in the quantum vacuum energy.

Calculating Casimir forces in a classical finite-difference time-domain (FDTD) Maxwell simulation like Meep is possible because of a new algorithm described in:

Alejandro W. Rodriguez, Alexander P. McCauley, John D. Joannopoulos, and Steven G. Johnson, "Casimir forces in the time domain: I. Theory," arXiv preprint archive article arXiv:0904.0267 (April 2009).
Alexander P. McCauley, Alejandro W. Rodriguez, John D. Joannopoulos, and Steven G. Johnson, "Casimir forces in the time domain: II. Applications," arXiv preprint archive article arXiv:0906.5170 (June 2009).

These papers describe how any time-domain code may be used to efficiently compute Casimir forces without modification of the internal code. The newest version of Meep contains several optimizations of these algorithms, allowing for very rapid computation of Casimir forces (reasonably-sized two-dimensional systems can be solved in a matter of seconds).

This page will provide some tutorial examples showing how these calculations are performed for simple geometries. For a derivation of these methods, the reader is referred to the papers above, which will be referred to as Part I and Part II in this webpage.

Introduction

In this section, we introduce the equations and basic considerations involved in computing the force using the method presented in Rodriguez et. al. (arXiv:0904.0267). Note that we keep the details of the derivation to a minimum and instead focus on the calculational aspects of the resulting algorithm.

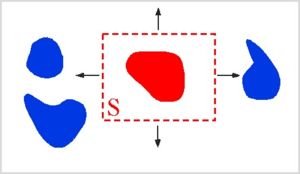
The general setup for a Casimir force computation is shown in the following figure:

The goal is to determine the Casimir force on one object (shown in red) due to the presence of other objects (blue).

Classically, the force on red object due to the electromagnetic field can be computed by integrating the Maxwell stress tensor $''' M''' i j$ (ref: Griffiths) over frequency and over any surface enclosing only that object, shown below:

The classical force is then:

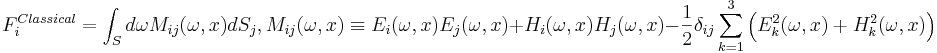
$F_i^{Classical} = \int_S d\omega M_{ij}(\omega,x) dS_j, M_{ij}(\omega,x) \equiv E_i(\omega,x)E_j(\omega,x) + H_i(\omega,x)H_j(\omega,x) - \frac{1}{2}\delta_{ij}\sum_{k=1}^3 \left(E_k^2(\omega,x) + H_k^2(\omega,x) \right)$

[ref] showed the the Casimir force can be obtained by a similar integral, except that the stress tensor is replaced with the expectation value of the corresponding operator in the quantum-mechanical grounds state of the system:

Failed to parse (unknown error): F_i^{Casimir} = \int_S d\omega \left{ M_{ij}(\omega,x) dS_j

The basic steps involved in computing the Casimir force on an object are:

1. Surround the object for which the force is to be computed with a simple, closed surface $S$ . It is often convenient to make $S$ a rectangle in two dimensions and a rectangular prism in three dimensions. This is illustrated below:

In this calculation, we determine the force on the object (shown in red) due to the presence of other objects (blue).

2. Add a uniform, frequency-independent conductivity $σ$ to the dielectric response of every object (which is easily done Meep). The purpose of this is to rapidly reduces the time required for the simulations below.

3. Measure the electric E and magnetic H fields on $S$ in response to a set of different current distributions on $S$ (more on the specific form of these currents later).

4. Integrate these fields over the enclosing surface $S$ at each time step, and then integrate this result, multiplied by a known function $g ( - t)$ , over time $t$ .

The Casimir force is given by an expression of the form:

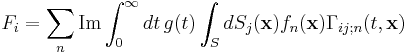
$F_i = \sum_n \mathrm{Im} \int_0^\infty dt \, g(t) \int_S dS_j(\textbf{x}) f_n(\textbf{x}) \Gamma_{ij;n}(t,\textbf{x})$

where $Γ i j; n$ are the fields in response to sources related to the functions $f n$ (discussed in detail later), $S$ is an arbitrary closed surface enclosing the object for which we want to compute the Casimir force, $g (t)$ is a known function, and the index $n$ ranges over all of the integers.

Note that the precise implementation of step (3) will greatly affect the efficiency of the method. For example, computing the fields due to each source at each point on the surface separately requires a separate Meep calculation for each source (and polarization). As described in Part II (arXiv:0906.5170), and further below, it is possible to modify these steps in order to optimize the calculation of the stress tensor over the spatial surface. For the purpose of this introduction, however, we do not require specific details on how we handle the spatial integration.

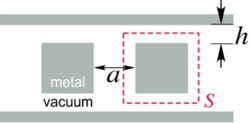
Example: two-dimensional blocks

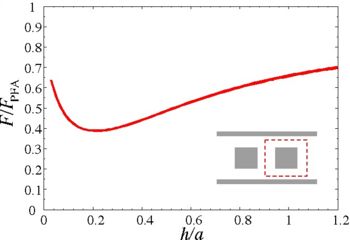
In this section we calculate the Casimir force in the two-dimensional double-block configuration (Rodriguez et. al, Physical Review Letters, vol 99, p 080401 2007) shown below:

The dashed red lines indicate the surface $S$ . This system consists of two metal $a\times a$ squares in between metallic sidewalls. As described in Part II, the first step is to add a uniform, frequency-independent D-conductivity $σ$ to all the dielectrics (in this case metal and vacuum):

 (define-param Sigma 1)
 (define my-metal (make material (epsilon -1e20) (D-conductivity Sigma)))
 (define my-air   (make material (epsilon -1e20) (D-conductivity Sigma)))
 (set! default-material my-air)

As discussed in Part I, the optimal value of $σ$ depends on the system under consideration. In our case, $σ = 1$ appears to be optimal or near optimal.

We then add in the double blocks:

 (set! geometry 
       (list (make block (center   a   0) (size a a infinity) (material my-metal))
             (make block (center (- a) 0) (size a a infinity) (material my-metal))))

As described in Part I, one way to evaluate both the electric and magnetic field contributions to the force is to run two separate simulations, one with electric field sources, and then another with the same sources, but with the permittivity 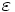$\varepsilon$ and permeability $μ$ interchanged. Then when we run the magnetic field contribution, everything will be identical except for the definition of my-metal above.

In the ideal system the empty space extends to infinity in both the left and right directions. For a finite computational cell, we define a horizontal buffer region xbuffer and impose periodic boundary conditions in $x$ and metallic boundary conditions in $y$ :

 (set! geometry-lattice (make lattice (size (+ (* 3 a) (* 2 xbuffer)) (+ a (* 2 h)) no-size)))

When imposing the boundary conditions, it is important to first initialize the fields in Meep:

 (init-fields)
 (meep-fields-use-bloch X 0)

Note that this is different from (set! k-point (vector3 0)) as this will assign periodic boundary conditions to both $x$ and $y$ .

Defining the sources

We then define the surface $S$ through lists containing the centers and sizes of each side of $S$ :

 (define block-cen (vector3 a 0 0))
 (define xshift (vector3 (/ L 2)   0   ))
 (define yshift (vector3    0   (/ L 2)))

 (define face-centers 
   (list (vector3- block-cen xshift) (vector3+ block-cen xshift)
         (vector3- block-cen yshift) (vector3+ block-cen yshift)))
 (define face-sizes
   (list (vector3 0 L) (vector3 0 L) (vector3 L 0) (vector3 L 0)))
 (define face-orientations (list -1 1 -1 1))

This contains all the information about $S$ and can be used for many two-dimensional Casimir force calculations. The last list of orientations is required to evaluate $d S j$ in the integral over $S$ and represents the outward normal orientation on the square surface.

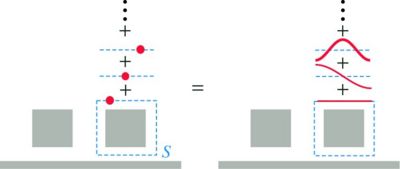
As described in Part II, the next step is to pick a basis of functions ${f n}$ on $S$ , indexed by $n$ , such that these form a complete and orthonormal basis for all real-valued functions on $S$ . Since $S$ consists of four distinct line segments, we take a real cosine basis:

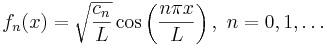
$f_n(x) = \sqrt{\frac{c_n}{L}} \cos \left(\frac{n\pi x}{L}\right), ~n = 0,1,\ldots$

where $c n = 1$ if $n = 0$ and $c n = 2$ otherwise, $L$ is the side length (if each side has a different length, then the functions $f n (x)$ will differ for each side). An illustration of these functions for the system under consideration is shown on the right.

As shown in the figure, any set of basis functions will give the same force once every function is included. One can equally well compute the force using a basis where each $f n$ is a $δ$ function. However, one would require many different point sources to get an accurate answer, whereas the cosine basis above requires only a few values of $n$ before the answer has converged to high accuracy (this is discussed further in Part II).

For the present example, the functions $f n (x)$ are easily defined in the ctl file:

 (define (dct X n source-size)
   (let*
      ((X-start (vector3+ X (vector3-scale 0.5 face-size))))
       (x (vector3-x X-start))
       (y (vector3-y X-start))
       (kx (/ (* n pi) L))
       (ky (/ (* n pi) L)))
   (* (sqrt (/ (if (= n 0) 1 2) L)) (cos (* kx x)) (cos (* ky y))))

The reason for the shift from X to X-start is that the origin of the dct functions is the endpoint of the line segment, while the origin for a function (amp-func ...) is taken to be the center of the surface. Also, we are allowed to insert both (cos (* kx x)) and (cos (* ky y)), even though the face is actually one-dimensional. This is because, if the surface has zero size in one direction, that coordinate will always be zero (since the coordinates are relative to the center of the face), so the (cos ...) term in that direction will always be 1. Writing things this way merely simplifies the Scheme code.

A simulation is run for each $n$ , each side of $S$ , indexed by the integer side, and each source polarization. The source itself has the form:

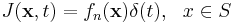
$J(\textbf{x},t) = f_n(\textbf{x}) \delta(t),~~x \in S$

This is defined using the custom-src function:

 (define (update-sources)
   (change-sources!
      (list (make source
              (src (make custom-src
                     (src-func (lambda (t) (if (= t (* 1.5 dt)) (/ 1 dt) 0)
                     (is-integrated? false) (start-time (- infinity)) (end-time 1)))
              (center (list-ref face-centers side)) (size (list-ref face-sizes side))
              (component current-pol) (amplitude 1)
              (amp-func (lambda (X) (dct X n (list-ref face-sizes side)))))))

where dt is the unit of time-stepping given by (meep-fields-dt-get fields).

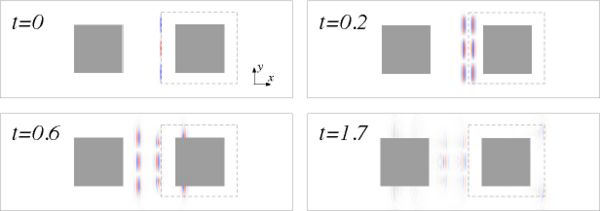
To illustrate the field profiles, below we show four snapshots at different times for what we term 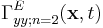$\Gamma^E_{yy;n=2}(\textbf{x},t)$ , the $y$ -component of the electric field response to a $y$ -polarized current source with spatial dependence $f 2 (x)$

At each time-step, the fields are integrated over $S$ , weighted by both $f n (x)$ and $g (t)$ , yielding a differential increment in the force as a function of time:

$dF_{n} = \mathrm{Im}[g(t)] \int_S dS_j(\textbf{x}) f_n(\textbf{x}) \Gamma_{ij;n}(t,\textbf{x})$

Computation of $g (t)$

As discussed in Part I, the function $g (t)$ is directly computed as the Fourier transform of a function of real frequency $ξ$ , $g (ξ)$ . This function is given by:

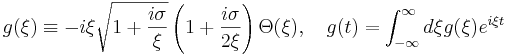
$g(\xi) \equiv -i\xi\sqrt{1 + \frac{i \sigma}{\xi}}\left(1+\frac{i \sigma}{2\xi}\right)\Theta (\xi), ~~~ g(t) = \int_{-\infty}^\infty d\xi g(\xi)e^{i\xi t}$

This Fourier transform can be computed numerically. However, as discussed in Part II, $g (ξ)$ diverges in both the low- $ξ$ and high- $ξ$ limits, making numerical computation of the transform cumbersome. A method around this issue (discussed in the appendix of Part II) is to subtract off these asymptotic terms and evaluate their Fourier transforms analytically. The remaining function is bounded for all frequency and is easily handled numerically.

A Fourier transform is still clumsy to implement directly through the Scheme front-end. This is why, in the newest release of Meep, we have included a function (make-casimir-g ...) which will return a list whose values are $g (t)$ where $t$ is given in increments of the time-domain simulation $d t$ :

 (define gt (make-casimir-g T dt Sigma [eps-omega] [Tfft]))

Here T is the total simulation time, and the optional argument eps-omega accounts for dispersive materials (the influence of dispersion is discussed in Part I) and Tfft controls the frequency resolution of the Fourier transform ( $d ξ˜1 / T FFT$ ). By default, eps-omega is NULL and Tfft equals $10 T$ . For many cases, however, $T < 50$ is often sufficient to obtain high convergence. In this case, a value of Tfft on the order of $103$ or greater is recommended.

Integration of the fields

As with the construction of $g (t)$ , the integration of the fields along $S$ , weighted by the function $f n (x)$ , can be done in any version of meep through the Scheme interface. However, in this form, every pixel communicates through the Scheme interpreter at every timestep. This significantly slows down computation time; in fact, in two dimensions it dominates the actual time-stepping for resolutions below 400!

To circumvent this, the newest version of meep also has a built-in field-integration routine, (meep-fields-casimir-stress-dct-integral ...), which will automatically integrate the field response $Γ i j; n$ along a specified face of $S$ . This value is then added to the current force in direction $x$ .

We compress both of these steps into one function, (integrate-function), which will be called at every time step:

 (define counter 0)

 (define (integrate-function)
     (set! Gamma-integral-X
        (meep-fields-casimir-stress-dct-integral fields X current-dir n n 0 E-stuff current-face))
     (set! Force-x
        (+ Force-x (* dt 
                     (imag-part (list-ref gt counter)) 
                     current-orientation
                     Gamma-integral-X))
    (set! counter (+ counter 1)))

Now define a procedure for running a simulation for each side of $S$ for each electric field polarization curr-pol:

 (define (run-one-simulation curr-pol)
   (begin
       (set! current-pol curr-pol)
       (do ((i 0 (1+ i))) ((= i (length face-centers))) ;Faces of S
          (begin
             (update-sources)
             (set! current-face (volume (center (list-ref face-centers i)) (size (list-ref face-sizes i))))
             (run-until Tmax integrate function)
             (restart-fields) (set! counter 0)))))

The appropriate run time $T$ depends upon the system under consideration. The the example of the double blocks, we find that by $T = 40$ the force has converged to within 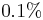$0.1\%$ of its final value.

Now we simply run one of these simulations for each polarization:

 (define pols-list (list Ex Ey Ez))
 (map run-one-simulation pols-list)

Magnetic field contribution

As discussed above, we must now run a separate set of simulations to get the contribution from magnetic sources. This is easily done in Meep by resetting the geometry so that 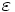$\varepsilon$ and $μ$ are switched:

 (reset-meep)

 (set! my-metal (make medium (epsilon 1) (mu -1e20) (D-conductivity Sigma))
 (set! default-material my-air)
 (set! geometry 
       (list (make block (center   a   0) (size a a infinity) (material my-metal))
             (make block (center (- a) 0) (size a a infinity) (material my-metal))))

 (map run-one-simulation pols-list)

Notice that we still use a D-conductivity, rather than a B-conductivity as one might expect; remember that this conductivity is introduced as a mathematical construction. The physical system has no dissipation, and the appropriate way to input the conductivity is in this form (this is discussed in Part I). Otherwise, the simulation proceeds exactly as before.

Results

The result, when sampled over many values of $h$ , is a force curve that varies non monotonically in $h$ :

Using the optimizations discussed above, it takes roughly 20 seconds to run simulation at resolution 40 for each value of $n$ , including all sides of $S$ and all field polarizations. Typically, only 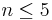$n\leq 5$ are needed to get the force to high precision, so the Casimir force for this system can be determined in under two minutes on a single processor

Example: dispersive materials

[coming soon]

Example: cylindrical symmetry

[coming soon]

Example: three-dimensional computations

[coming soon]

Retrieved from "http://ab-initio.mit.edu/wiki/index.php/Casimir_calculations_in_Meep"

Category: Meep

Casimir calculations in Meep

From AbInitio

Revision as of 16:53, 31 August 2009

Contents

Computing Casimir forces with Meep

Introduction

Example: two-dimensional blocks

Defining the sources

Computation of $g (t)$

Integration of the fields

Magnetic field contribution

Results

Example: dispersive materials

Example: cylindrical symmetry

Example: three-dimensional computations

Views

Personal tools

Navigation

Search

Toolbox

 The classical force is then:
-<math> F_i^{Classical} = \int_S d\omega M_{ij}(\omega,x) dS_j,    M_{ij}(\omega,x) \equiv E_i(\omega,x)E_j(\omega,x) + H_i(\omega,x)H_j(\omega,x) - \frac{1}{2}\delta_{ij}\sum_{k=1}^3 \left(E_k^2(\omega,x) + H_k^2(\omega,x) \right) </math>
+<math> F_i^{Classical} = \int_S d\omega M_{ij}(\omega,x) dS_j,       M_{ij}(\omega,x) \equiv E_i(\omega,x)E_j(\omega,x) + H_i(\omega,x)H_j(\omega,x) - \frac{1}{2}\delta_{ij}\sum_{k=1}^3 \left(E_k^2(\omega,x) + H_k^2(\omega,x) \right) </math>
 [ref] showed the the Casimir force can be obtained by a similar integral, except that the stress tensor is replaced with the expectation value of the corresponding operator in the quantum-mechanical grounds state of the system:

Casimir calculations in Meep

From AbInitio

Revision as of 16:53, 31 August 2009

Contents

Computing Casimir forces with Meep

Introduction

Example: two-dimensional blocks

Defining the sources

Computation of g(t)

Integration of the fields

Magnetic field contribution

Results

Example: dispersive materials

Example: cylindrical symmetry

Example: three-dimensional computations

Views

Personal tools

Navigation

Search

Toolbox

Computation of $g (t)$