Waveguide Crossings

Perfect Waveguide Intersections

In constructing integrated optical "circuits," space constraints and the desire for complex systems involving multiple waveguides necessitate waveguide crossings. We propose a novel method for intersecting waveguides with negligible crosstalk. Moreover, this technique depends on general symmetry considerations that can be applied to almost any system a priori, with little need for manual "tuning."

The basic idea is to consider coupling of the four branches, or "ports" of the intersection in terms of coupling through a resonant cavity at the center. If the resonant cavity can be prevented by symmetry from decaying into the crossing waveguide, then the situation reduces to one-dimensional resonant tunnelling, and crosstalk will be prohibited. This situation is achieved by requiring simple symmetries in the waveguide and resonant modes, as shown below:

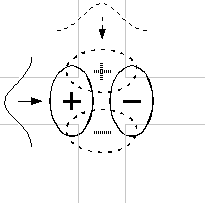
Here, the solid-line waveguide modes only couple with the solid-line resonant cavity modes, and similarly for the dashed-line modes. Essentially, there are three requirements that must be met:

The waveguides must have mirror symmetry about their axis, and they must be single-mode in the frequency range of interest. (This mode will be either even or odd.)
The resonant cavity in the center of the intersection, which governs coupling between the waveguides, must respect the mirror planes of both waveguides.
In the frequency range of interest, the resonant modes must be odd with respect to one waveguide and even with respect to the other.

All three of these conditions are easily achieved. (In particular, the third condition is automatic for degenerate modes in intersections with sufficient symmetry [the symmetry group of the square].) The resulting transmission profile will be the typical spectrum of resonant tunneling--a Lorentzian (bell-shaped) curve centered on the resonance frequency. The width of the resonance is inversely proportional to the quality factor Q of the resonant mode (Q is proportional to the decay lifetime).

For a demonstration of how this works, we have put together a couple of animations (in QuickTime format) showing waveguide intersections in operation. These animations are for two-dimensional systems, but the same principle works in three dimensions.

First, let us examine an intersection of two waveguides in a photonic crystal consisting of a square lattice of dielectric rods in air. Photonic crystals are an ideal way to make such a crossing because they prevent the possibility of any radiation loss. It is also easy to make a resonant cavity of any desired frequency and symmetry simply by tuning the radius of a single defect rod.

If we simply cross two waveguides (formed by removing a row or column of rods), there is significant crosstalk, as shown below. (Both transmission and crosstalk are in the 30-40% range.) The animation depicts the z-component of the electric field for an incident TM wave from the left; positive and negative values are indicated by blue and red. The contours of the dielectric are shown in black. Note that there is significant reflection from the intersection.

You can also download this movie (1.1 MB).

The same intersection, however, with a resonant cavity at the center (supporting a pair of dipole-like modes), dramatically reduces crosstalk to only 0.04%. (The reflection is of a similar order.) Shown below is light passing through this intersection at the peak transmission frequency:

You can also download this movie (1.1 MB).

The above examples were for photonic crystal waveguides, but identical principles apply to crossings of conventional (index-contrast) waveguides. Again, we merely need to put a resonant cavity at the center of the intersection having modes of the appropriate symmetry.

Below, we show light passing throug an intersection of conventional waveguides in which our design has been applied. (In this case, we use TE light and show the z-component of the magnetic field.) To create a resonant cavity, we make a periodic sequence of three air holes on each branch of the crossing, forming a one-dimensional photonic crystal that can confine a cavity mode. Here, the crosstalk is only 0.08%, versus 7% crosstalk in the same intersection without holes.

You can also download this movie (181 kB).

Because there is no photonic crystal surrounding these waveguides, radiation losses are present due to scattering off the intersection. These losses only have the effect of decreasing transmission, however, and do not increase crosstalk. Thus, in this case the transmission is only 92%. (Radiation losses could be reduced, if necessary, since there are many parameters available for tuning the shape of the intersection without affecting crosstalk.)

For comparison, here is the same intersection without the holes or the resonant cavity, in which the 7% crosstalk is readily apparent.:

You can also download this movie (263 kB).

Resonant cavities that don't use photonic crystals can also be used. (For example, they can operate by index-confinement.)

For more information, see the paper "Elimination of cross talk in waveguide intersections," in Optics Letters 23, pp. 1855-1857 (December 1998).