Synthesis and observation of
non-Abelian gauge fields in real space
|
|
|
Background on non-Abelian gauge
fields Gauge fields are the backbone of
gauge theories, the earliest example of which is classical electrodynamics.
Gauge fields can be classified as Abelian (commutative) or non-Abelian
(noncommutative), depending on the commutativity of the underlying group. In
the standard model, fundamental particles typically interact with each other
via non-Abelian gauge fields. For charge-neutral particles,
such as photons and cold atoms, synthetic gauge fields can be created by
experimental design to affect the dynamics, especially the geometric phases,
of the physical systems. So far, real-space synthesis of gauge fields have
been limited to Abelian ones.
The famous Aharonov–Bohm
effect [Y. Aharonov, D. Bohm, Phys. Rev. 115, 485–491
(1959)] proved that the associated geometric phase is indeed observable,
making gauge fields not only accessory, but essential to our understanding of
physical systems. In the original Aharonov–Bohm effect, a particle experience an Abelian
(commutative) gauge potential, which imprints a scalar, observable geometric
phase in its wave function. The non-Abelian (non-commutative) generalization
of the Aharonov–Bohm effect was initially conceived
as a thought experiment to probe non-Abelian gauge fields [T. T. Wu, C. N.
Yang, Phys. Rev. D 12, 3845–3857 (1975)]. Since then, this non-Abelian effect
has generated persistent interest among almost all branches of physics for
its own importance and innumerable implications.
Our paper reports the first
experimental synthesis of real-space non-Abelian gauge fields, which enables
us to also make the first-ever observation of the non-Abelian Aharonov-Bohm effect. We synthesize tunable non-Abelian
gauge fields in real space by breaking time-reversal symmetry, differently,
in two orthogonal bases (linear and circular) of the Hilbert space spanned by
photons in a mode degeneracy.
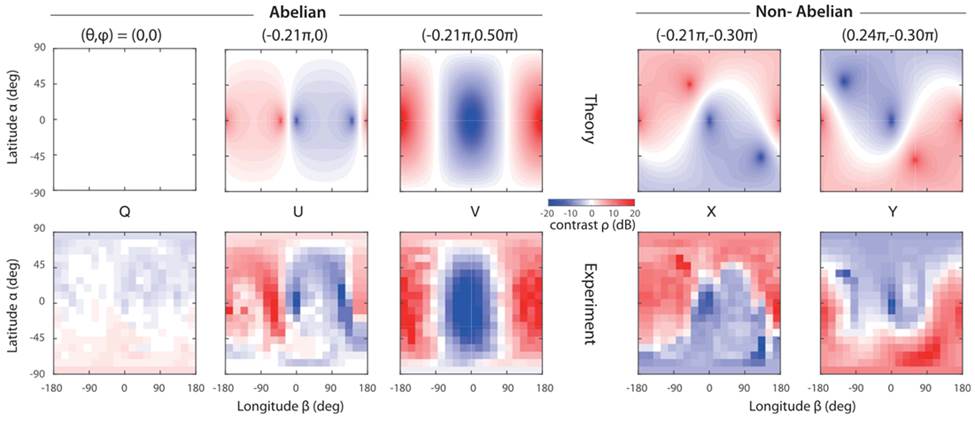
Figure.
Non-Abelian Aharonov–Bohm interference on the Poincaré sphere.
In our measurement, an off-equator pole/zero of the interference contrast is
the key indicator of non-Abelian gauge fields (compare Abelian cases Q, U,
and V with non-Abelian cases X and Y). Yi Yang, Chao Peng, Di
Zhu, Hrvoje Buljan, John
D. Joannopoulos, Bo Zhen, and Marin Soljačić, Synthesis and observation of non-Abelian gauge fields
in real space, Science, 365, 1021 (2019)
The following works are
particularly related to ours: [1] J. Ruseckas, G. Juzeliūnas, P. Öhberg, M. Fleischhauer, Phys. Rev. Lett. 95, 010404 (2005). [2] K. Osterloh, M. Baig, L. Santos, P. Zoller, M. Lewenstein, Phys. Rev. Lett. 95, 010403 (2005). [3] J. Dalibard, F. Gerbier, G. Juzeliūnas, P. Öhberg, Rev. Mod. Phys. 83, 1523–1543 (2011). [4] N. Goldman, G. Juzeliūnas,
P. Öhberg, I. B. Spielman,
Rep. Prog. Phys. 77, 126401 (2014). [5] T. Iadecola, T. Schuster,
C. Chamon, Phys. Rev. Lett. 117, 073901 (2016). [6] Y. Chen, R.Y. Zhang, Z. Xiong,
Z.H. Hang, J. Li, J.Q. Shen, and C.T. Chan, Nat. Commun. 10,
3125 (2019). |