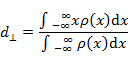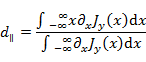A general theoretical and experimental framework for nanoscale electromagnetism

Background on nonclassical corrections in nanophotonics

Local, bulk response functions, e.g. permittivity, and the macroscopic Maxwell equations completely specify the classical electromagnetic problem, which features only wavelength and geometric scales. They have proven extremely successful at macroscopic length scales, across all branches of photonics. Even state-of-the-art nanoplasmonic studies, exemplars of extremely interface-localized fields, rely on their validity.

 

This classical description, however, neglects the intrinsic electronic length scale associated with interfaces. This omission leads to significant discrepancies between classical predictions and experimental observations in systems with deeply nanoscale feature sizes, typically evident below ∼10 – 20 nm.


Background on the Feibelman d parameters

The d parameters, first introduced by Feibelman, are a convenient mathematical parametrization for surface-related, quantum corrections. They can be derived from a careful analysis of the reflection of an external potential off a planar interface by going beyond the conventional assumptions of local and stepwise material response: the d parameters then introduce the leading-order corrections to the classical reflection coe
fficients.

 

The Feibelman and parameters play a role analogous to the local bulk permittivity, but for interfaces between two materials. and are equal to the frequency-dependent centroids of the induced charge and the normal derivative of the tangential current, respectively, at an equivalent planar interface. Mathematically, their definitions are given by

 

where  is the induced charge,  is the induced current, and  and  are out-of-plane and in-plane directions, respectively.

 

The d parameters enable a leading-order-accurate incorporation of nonlocality, spill-out, and surface-enabled Landau damping (tunnelling and size quantization, which are not incorporated in the d parameters, are non-negligible at feature sizes below about 1 nm).

Mesoscopic boundary conditions

The d parameters drive an effective nonclassical surface polarization with  contributing an out-of-plane surface dipole density π(r) and  contributing an in-plane surface current density K(r).

These surface terms can be equivalently incorporated as a set of mesoscopic boundary conditions (here without external interface currents or charges) for the conventional macroscopic Maxwell equations, as summarized below. Evidently, the mesoscopic boundary conditions reduce to the classical boundary conditions in the limit  .

 

 

Classical electromagnetism

 

 

Nanoscale Electromagnetism

 

Numerical solver

We implemented the mesoscopic boundary conditions in a standard full-wave numerical solver COMSOL Multiphysics. Our implementation and a few numerical examples are available at https://github.com/yiy-mit/nanoEM

 

In the numerical implementations, we include plane-wave scattering solutions for cylinders, bowtie antennas, spheres, and film-coupled nanodisks. They can be generalized to other electromagnetic problems such as normal/quasinormal mode problems, spontaneous emission, near-field scanning microscopy, electron energy loss spectroscopy, and more.


Measurement of the d parameters

We  establish  a  systematic  approach  to measure the d parameter dispersion of a general two-material interface,  and  illustrate  it  for  Au–AlOx interfaces.

 

We  translate the mesoscopic d parameter directly into observables—spectral  shifting  and  broadening—and  measure  them  in  specially designed  plasmonic  systems  that  exhibit  pronounced  nonclassical  corrections.  Our  experimental  testbed  enables  a  direct procedure  to  extract d parameters  from  standard  dark-field measurements, in a manner analogous to ellipsometric measurements of the local bulk permittivity.

 

Moreover, by investigating a complementary hybrid plasmonic setup, we discover and  experimentally  demonstrate  design  principles  for  structures that are classically robust—i.e. exhibit minimal nonclassical corrections—even under nanoscopic conditions.

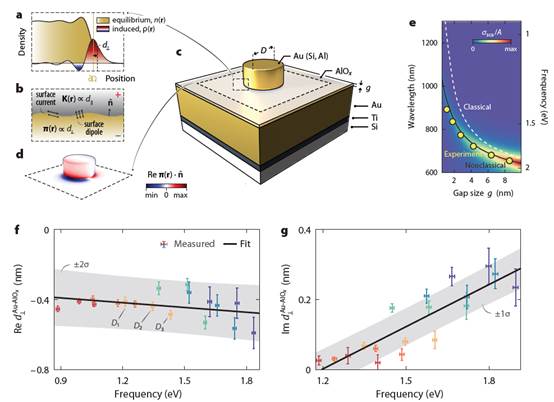
Framework, experimental structure, measured nonclassical shifts, and surface response

dispersion. a. Equilibrium and induced densities.  is the centroid of induced charge.

b. Nonclassical corrections can be formulated as self-consistent surface polarizations, representing effective surface dipole density π(r) and current density K(r). c. Experimental structure. d. Nonclassical surface dipole density π(r) of the fundamental dipolar gap plasmon of a film-coupled Au nanodisk. e. Observation of large nonclassical corrections (spectral shift ~400 nm) in film-coupled Au nanodisks. Measured frequencies (circles) of the resonance blueshift relative to the classical prediction (dashed line) and quantitatively agree with nonclassical calculations. f–g. Measured (markers) dispersion of  (f),  (g), and their linear fits (lines).

 

 

 

Yi Yang, Di Zhu, Wei Yan, Akshay Agarwal, Mengjie Zheng, John D. Joannopoulos, Philippe Lalanne, Thomas Christensen, Karl K. Berggren, Marin Soljačić, arXiv: 1901.03988. Nature. doi:10.1038/s41586-019-1803-1



Press coverages include Phys.org, Science Daily, Nanowerk, EurekAlert!, Tech Explorist, Bioengineer, and DeepTech深科技.

 

Related works

The following works are particularly related:

 

[1]     P.J. Feibelman, Prog. Surf. Sci. 12, 287 (1982).

A.      Liebsch, Electronic Excitations at Metal Surfaces, Physics of Solids and Liquids (Springer, 1997).

[2]     P. Apell and A. Ljungbert, Physica Scripta 26, 113 (1982).

[3]     N. A. Mortensen, S. Raza, M. Wubs, and S. I. Bozhevolnyi, Nat. Commun. 5, 3809 (2014).

[4]     W. Yan, M. Wubs, and N. A. Mortensen, Phys. Rev. Lett. 115, 137403 (2015).

[5]     W. Zhu, R. Esteban, A.G. Borisov, J.J. Baumberg, P. Nordlander, H.J. Lezec, J. Aizpurua, and K.B. Crozier, Nat. Commun. 7, 11495 (2016).

[6]     T. Christensen, W. Yan, A.-P. Jauho, M. Soljačić, and N.A. Mortensen, Phys. Rev. Lett. 118, 157402 (2017).

[7]     Y. Yang, O.D. Miller, T. Christensen, J.D. Joannopoulos, and M. Soljačić, Nano Lett. 17, 3238 (2017).

[8]     P. Lalanne, W. Yan, K. Vynck, C. Sauvan, and J.-P. Hugonin, Laser Photonics Rev. 12, 1700113 (2018).