Shrinking light to allow forbidden transitions on the atomic scale

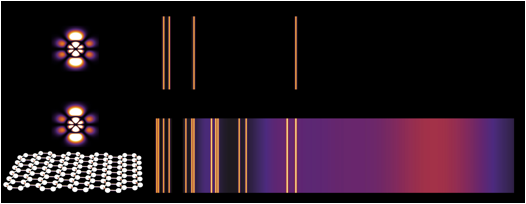
Emission spectra. An illustration of the different frequencies of light that can be emitted by an atom in a high energy state far away from graphene (top) or a few nanometers away from graphene doped with charge carriers (bottom). The emission spectra are based on a lithium atom initially excited from a 2s orbital to a 5f orbital, and then subsequently decaying to any unoccupied lower energy level. [For the continuous spectra, the colors represent the relative probability of emission at that frequency. For each transition, an orange line (or purple cloud) was placed if that transition is estimated to be faster than 1 per microsecond.]

Background on Forbidden Transitions and Spontaneous Emission

One of the most fundamental avenues of study in controlling light-matter interactions is engineering of the spontaneous emission rates of excited electrons in emitters (atoms, molecules, artificial atoms, etc.). In general, the spontaneous emission is modified by placing the emitter in an optical environment different from free-space, such as an optical resonator with a high quality factor or a low modal volume.

Despite being a topic of great interest, spontaneous emission engineering is almost exclusively considered in the framework of single-photon dipole (E1) transitions; those in which the orbital angular momentum of the electron changes by one and a single photon is emitted. Transitions in which either: the orbital angular momentum changes by n > 1 (En transitions), the spin of the electron flips, or multiple photons are emitted are simply ignored. This is for good reason. In atomic emitters, the rate of one-photon multipole (En) transitions scales as:

where is the characteristic size of the emitter while is the wavelength of the emitted electromagnetic radiation, and is the fine-structure constant. Because , non-dipole transitions are highly suppressed, leading to the famous dipole selection rules. Similarly, two-plasmon transitions (occurring through intermediate dipole transitons) have rates scaling like making them much slower than single-photon dipole transitions.

2D Plasmons and New Realms of Light-Matter Interactions

In our work [1], we considered the effect of plasmons in 2D materials such as graphene to enable conventionally forbidden transitions. Plasmons in graphene are electromagnetic waves which are confined to the surface of graphene. Their wavelength is much shorter than that of free-space photons at the same frequency, by a factor called the confinement factor, defined as . The principle of our work is very simple. 2D plasmons quantum mechanically behave like conventional far-field photons, so much so, that the estimates provided above for forbidden transition rates can easily be revised. They now become:

and

Because the confinement ( of graphene plasmons being in excess of 200, it is possible to get rates enhancements of quadrupole transitions in excess of ten billion (meaning that they can happen in nanoseconds). Two-plasmon emissions can be enhanced by fifteen orders of magnitude, leading to them potentially happening on picosecond time scales, in stark contrast to minutes in free space. Graphene’s unprecedentedly high photonic LDOS in addition to its unprecedentedly high confinement allows for access to forbidden transitions at extremely fast rates. E5 transitions, where the orbital angular momentum of the electron changes by 5 (as for a transition between s and h orbitals), can happen in hundreds of nanoseconds. In free-space, these transitions take place on time scales comparable to the age of the universe.

In other words, the basic constraints which have dictated studies of light-matter interaction thus far become invalidated, allowing for a plethora of qualitatively new light-matter interaction processes, and the design of new emitters.

References:

[1] Shrinking light to allow forbidden transitions on the atomic scale. N. Rivera, I. Kaminer, B. Zhen, J. D. Joannopoulos, and M. Soljacic. Science, 353, 6296 (2016).