|
Background on exceptional points
Undergraduate level textbooks teach us: “the eigenspace of a Hermitian operator always forms a complete basis.” The reversed question of this statement – what kind of non-Hermitian operators have an eigenspace that does not form a complete basis – is a much more complicated question. The answer to that question is: “when there are exceptional points.” Exceptional points (EPs) are special singularities unique to non-Hermitian systems, where two complex eigenvalues and their eigenvectors become the same. Since its introduction into optics and photonics, EPs have led interesting and counter-intuitive physical phenomena, including loss-induced transparency, unidirectional reflection, and unidirectional transmission. Background on Dirac cones The Dirac cone with its hallmark dispersion – two conical bands touching at a single point – started as a concept in particle physics. So far, Dirac cones have been successful realized in various material systems, including photons in waveguide arrays, atoms in optical lattices and electrons in graphene, leading to rich and interesting physics as well as important applications. As a result, Dirac cone have recently become one the focuses of research in condensed matter physics and material science. Connecting exceptional points and Dirac points Our experimental paper describes the observation of a ring of EPs being spawned from a Dirac point for an open system, where radiation loss need to be included 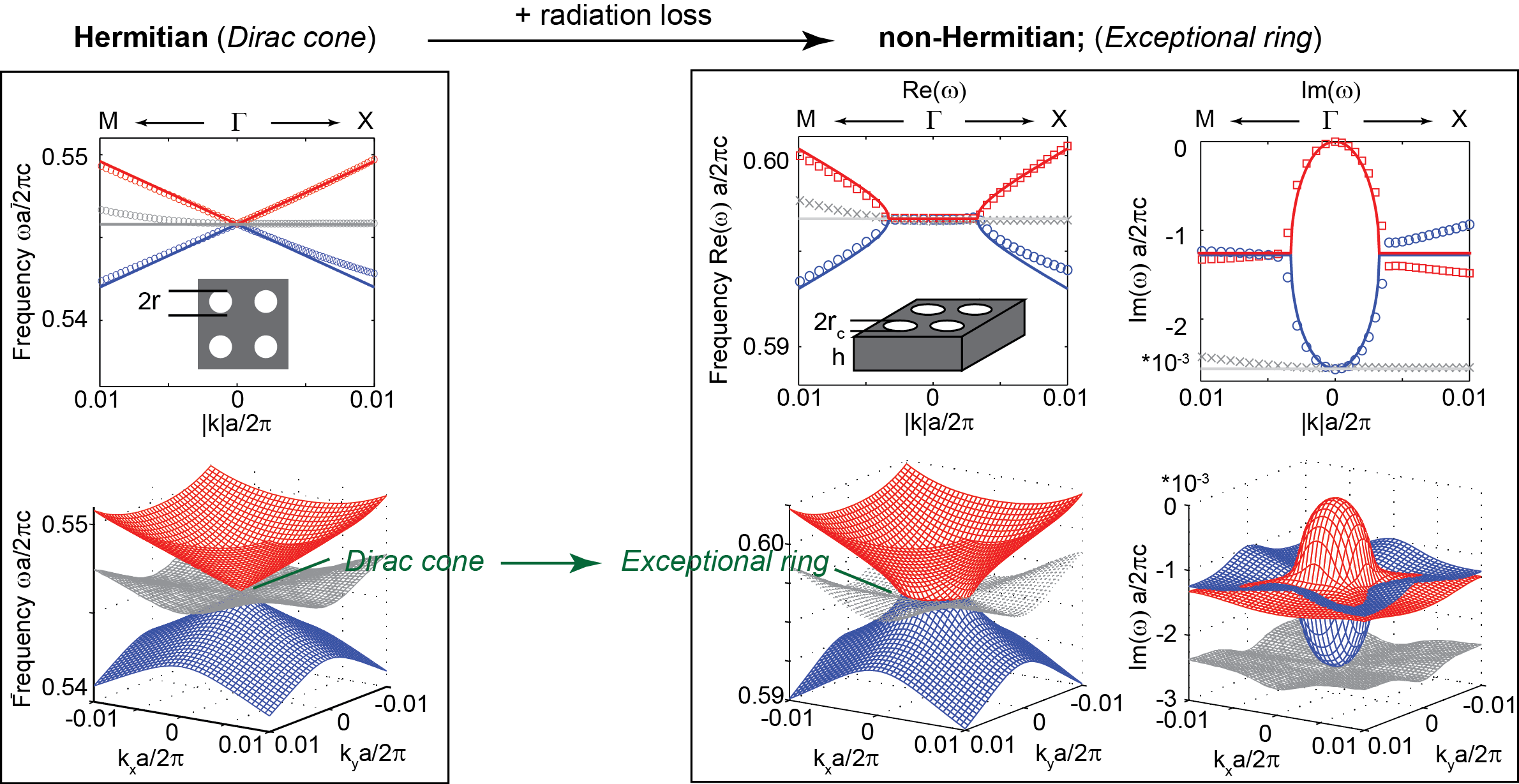 The study of EPs dates back to T. Kato’s book Perturbation theory of linear operators (1966). There have been many studies on EPs in recent years, particularly in the context of “parity-time symmetries”, ranging from electronics to electromagnetic and acoustic waves. The following works are particularly related to ours:
| ||