Synchronizing the magnetic and electric fields
From AbInitio
| Revision as of 16:14, 20 July 2008 (edit) Stevenj (Talk | contribs) ← Previous diff |
Revision as of 16:14, 20 July 2008 (edit) Stevenj (Talk | contribs) Next diff → |
||
| Line 1: | Line 1: | ||
| {{Meep}} | {{Meep}} | ||
| - | In the finite-difference time-domain method, the electric and magnetic fields are stored at ''different times'' (and different positions) in space, in a "[[w:Leapfrog integration|leap-frog]]" fashion. At any given time-step <math>t</math> during the simulation, the '''E''' and '''D''' fields are stored at time <math>t</math>, but the '''H''' and '''B''' fields are stored at time <math>t-\Delta t/2</math> (where <math>\Delta t</math> is the time-step size). | + | In the finite-difference time-domain method, the electric and magnetic fields are stored at ''different times'' (and different positions in space), in a "[[w:Leapfrog integration|leap-frog]]" fashion. At any given time-step <math>t</math> during the simulation, the '''E''' and '''D''' fields are stored at time <math>t</math>, but the '''H''' and '''B''' fields are stored at time <math>t-\Delta t/2</math> (where <math>\Delta t</math> is the time-step size). |
| This means that when you output the electric and magnetic fields from a given time step, for example, the fields actually correspond to times <math>\Delta t/2</math> apart. For most purposes, this slight difference in time doesn't actually matter much, but it makes a difference when you compute quantities like the Poynting flux <math>\mathbf{E}\times\mathbf{H}</math> that combine electric and magnetic fields together, e.g. for the <code>output-poynting</code> function. If what you really want is the Poynting flux <math>\mathbf{S}(t)</math> at time ''t'', then computing <math>\mathbf{E}(t)\times\mathbf{H}(t-\Delta t/2)</math> is slightly off from this — the error is of order <math>O(\Delta t)</math>, or first-order accuracy. This is unfortunate, because the underlying FDTD method ideally can have second-order accuracy. | This means that when you output the electric and magnetic fields from a given time step, for example, the fields actually correspond to times <math>\Delta t/2</math> apart. For most purposes, this slight difference in time doesn't actually matter much, but it makes a difference when you compute quantities like the Poynting flux <math>\mathbf{E}\times\mathbf{H}</math> that combine electric and magnetic fields together, e.g. for the <code>output-poynting</code> function. If what you really want is the Poynting flux <math>\mathbf{S}(t)</math> at time ''t'', then computing <math>\mathbf{E}(t)\times\mathbf{H}(t-\Delta t/2)</math> is slightly off from this — the error is of order <math>O(\Delta t)</math>, or first-order accuracy. This is unfortunate, because the underlying FDTD method ideally can have second-order accuracy. | ||
Revision as of 16:14, 20 July 2008
| Meep |
| Download |
| Release notes |
| FAQ |
| Meep manual |
| Introduction |
| Installation |
| Tutorial |
| Reference |
| C++ Tutorial |
| C++ Reference |
| Acknowledgements |
| License and Copyright |
In the finite-difference time-domain method, the electric and magnetic fields are stored at different times (and different positions in space), in a "leap-frog" fashion. At any given time-step t during the simulation, the E and D fields are stored at time t, but the H and B fields are stored at time t − Δt / 2 (where Δt is the time-step size).
This means that when you output the electric and magnetic fields from a given time step, for example, the fields actually correspond to times Δt / 2 apart. For most purposes, this slight difference in time doesn't actually matter much, but it makes a difference when you compute quantities like the Poynting flux  that combine electric and magnetic fields together, e.g. for the
that combine electric and magnetic fields together, e.g. for the output-poynting function. If what you really want is the Poynting flux 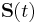 at time t, then computing
at time t, then computing 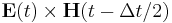 is slightly off from this — the error is of order O(Δt), or first-order accuracy. This is unfortunate, because the underlying FDTD method ideally can have second-order accuracy.
is slightly off from this — the error is of order O(Δt), or first-order accuracy. This is unfortunate, because the underlying FDTD method ideally can have second-order accuracy.
To improve the accuracy for computations involving both electric and magnetic fields, Meep provides a facility to synchronize the H and B fields with the E and D fields in time. Technically, what it does is to compute the magnetic fields at time t + Δt / 2 by performing a timestep, and then averaging those fields with the fields at time t − Δt / 2. This produces the magnetic fields at time t to a second-order accuracy of O(Δt2), which is the best we can do in second-order FDTD. Meep also saves a copy of the magnetic fields at t − Δt / 2, so that it can restore those fields for subsequent timestepping.
All of this process is handled for you in Meep by a single step function: synchronized-magnetic. By wrapping this around your step functions, it ensures that those step functions are called with synchronized electric and magnetic fields (to second-order accuracy), while restoring the magnetic fields automatically for subsequent timestepping.
For example, if you do:
(run-until 200 output-poynting output-tot-pwr)
it outputs the Poynting vector and the total energy density in the electric and magnetic fields at each timestep, but it only does so to first-order accuracy because those computations combine unsynchronized electric and magnetic fields. Instead, if you do
(run-until 200 (synchronized-magnetic output-poynting output-tot-pwr))
it will output the same quantities, but more accurately because the fields will be synchronized.
Alternatively, if you want to synchronize the magnetic and electric fields in some context other than that of a step function, e.g. you are doing some computation like integrate-field-function outside of the timestepping, you can instead call two lower-level functions. Before doing your computations, you should call (meep-fields-synchronize-magnetic-fields fields) to synchronize the magnetic fields with the electric fields, and after your computation you should call (meep-fields-restore-magnetic-fields fields) to restore the fields to their unsynchronized state for timestepping.
Note: in future versions of Meep, we may decide to synchronize the fields automatically whenever you output something like the Poynting vector or do a field integration that involves both magnetic and electric fields, but currently you must do this manually. (It doesn't hurt to nest the synchronization calls, so it is harmless to insert redundant field-synchronization calls.) The flux-in-box and field-energy-in-box routines are already automatically synchronized.

