NLopt Tutorial
From AbInitio
| Revision as of 15:15, 16 July 2010 (edit) Stevenj (Talk | contribs) (→Important: Modifying <code>grad</code> in-place) ← Previous diff |
Revision as of 15:15, 16 July 2010 (edit) Stevenj (Talk | contribs) (→Important: Modifying <code>grad</code> in-place) Next diff → |
||
| Line 370: | Line 370: | ||
| grad = 2*x | grad = 2*x | ||
| - | however, Python allocates a new array to hold <code>2*x</code> and reassigns grad to point to it, rather than modifying the original contents of grad. '''This will not work.'''' Instead, you should do: | + | however, Python allocates a new array to hold <code>2*x</code> and reassigns grad to point to it, rather than modifying the original contents of grad. '''This will not work.''' Instead, you should do: |
| grad[:] = 2*x | grad[:] = 2*x | ||
Revision as of 15:15, 16 July 2010
| NLopt |
| Download |
| Release notes |
| FAQ |
| NLopt manual |
| Introduction |
| Installation |
| Tutorial |
| Reference |
| Algorithms |
| License and Copyright |
In this tutorial, we illustrate the usage of NLopt in various languages via one or two trivial examples.
Contents |
Example nonlinearly constrained problem
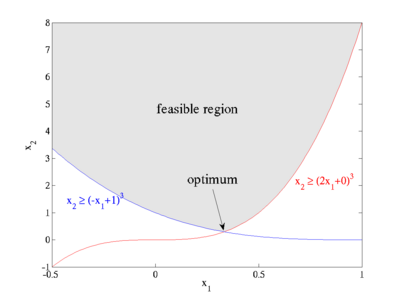
As a first example, we'll look at the following simple nonlinearly constrained minimization problem:
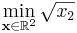
- subject to
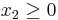 ,
, 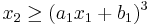 , and
, and 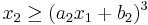
for parameters a1=2, b1=0, a2=-1, b2=1.
The feasible region defined by these constraints is plotted at right: x2 is constrained to lie above the maximum of two cubics, and the optimum point is located at the intersection (1/3, 8/27) where the objective function takes on the value 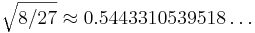 .
.
(This problem is especially trivial, because by formulating it in terms of the cube root of x2 you can turn it into a linear-programming problem, but we won't do that here.)
In principle, we don't need the bound constraint x2≥0, since the nonlinear constraints already imply a positive-x2 feasible region. However, NLopt doesn't guarantee that, on the way to finding the optimum, it won't violate the nonlinear constraints at some intermediate steps, while it does guarantee that all intermediate steps will satisfy the bound constraints. So, we will explicitly impose x2≥0 in order to ensure that the √x2 in our objective is real.
Note: The objective function here is not differentiable at x2=0. This doesn't cause problems in the examples below, but may cause problems with some other algorithms if they try to evaluate the gradient at x2=0 (e.g. I've seen it cause AUGLAG with a gradient-based solver to fail). To prevent this, you might want to use a small nonzero lower bound instead, e.g. x2≥10−6.
Example in C/C++
To implement the above example in C or C++, we would first do:
#include <math.h> #include <nlopt.h>
to include the NLopt header file as well as the standard math header file (needed for things like the sqrt function and the HUGE_VAL constant), then we would define our objective function as:
double myfunc(unsigned n, const double *x, double *grad, void *my_func_data)
{
if (grad) {
grad[0] = 0.0;
grad[1] = 0.5 / sqrt(x[1]);
}
return sqrt(x[1]);
}
There are several things to notice here. First, since this is C, our indices are zero-based, so we have x[0] and x[1] instead of x1 and x2. The return value of our function is the objective 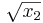 . Also, if the parameter
. Also, if the parameter grad is not NULL, then we set grad[0] and grad[1] to the partial derivatives of our objective with respect to x[0] and x[1]. The gradient is only needed for gradient-based algorithms; if you use a derivative-free optimization algorithm, grad will always be NULL and you need never compute any derivatives. Finally, we have an extra parameter my_func_data that can be used to pass additional data to myfunc, but no additional data is needed here so that parameter is unused.
For the constraints, on the other hand, we will have additional data. Each constraint is parameterized by two numbers a and b, so we will declare a data structure to hold this information:
typedef struct {
double a, b;
} my_constraint_data;
Then, we implement our constraint function as follows. (You always create a single constraint function, even if you have several very different constraints—your constraint function can do different things depending on what is passed as the void *data parameter.)
double myconstraint(unsigned n, const double *x, double *grad, void *data)
{
my_constraint_data *d = (my_constraint_data *) data;
double a = d->a, b = d->b;
if (grad) {
grad[0] = 3 * a * (a*x[0] + b) * (a*x[0] + b);
grad[1] = -1.0;
}
return ((a*x[0] + b) * (a*x[0] + b) * (a*x[0] + b) - x[1]);
}
The form of the constraint function is the same as that of the objective function. Here, the data parameter will actually be a pointer to my_constraint_data (because this is the type that we will pass to nlopt_minimize_constrained below), so we use a typecast to get the constraint data. NLopt always expects constraints to be of the form myconstraint(x) ≤ 0, so we implement the constraint x2 ≥ (a x1 + b)3 as the function (a x1 + b)3 − x2. Again, we only compute the gradient if grad is non-NULL, which will never occur if we use a derivative-free optimization algorithm.
Now, to specify this optimization problem, we create an "object" of type nlopt_opt (an opaque pointer type) and set its various parameters:
double lb[2] = { -HUGE_VAL, 0 }; /* lower bounds */
nlopt_opt opt;
opt = nlopt_create(NLOPT_LD_MMA, 2); /* algorithm and dimensionality */ nlopt_set_lower_bounds(opt, lb); nlopt_set_min_objective(opt, myfunc, NULL);
Note that we do not need to set an upper bound (nlopt_set_upper_bounds), since we are happy with the default upper bounds (+∞). To add the two inequality constraints, we do:
my_constraint_data data[2] = { {2,0}, {-1,1} };
nlopt_add_inequality_constraint(opt, myconstraint, &data[0], 1e-8); nlopt_add_inequality_constraint(opt, myconstraint, &data[1], 1e-8);
Here, the 1e-8 is an optional tolerance for the constraint: for purposes of convergence testing, a point will be considered feasible if the constraint is violated (is positive) by that tolerance (10−8). A nonzero tolerance is a good idea for many algorithms lest tiny errors prevent convergence. Speaking of convergence tests, we should also set one or more stopping criteria, e.g. a relative tolerance on the optimization parameters x:
nlopt_set_xtol_rel(opt, 1e-4);
There are many more possible parameters that you can set to control the optimization, which are described in detail by the reference manual, but these are enough for our example here (any unspecified parameters are set to innocuous defaults). At this point, we can call nlopt_optimize to actually perform the optimization, starting with some initial guess:
double x[2] = { 1.234, 5.678 }; /* some initial guess */
double minf; /* the minimum objective value, upon return */
if (nlopt_optimize(opt, x, &minf) < 0) {
printf("nlopt failed!\n");
}
else {
printf("found minimum at f(%g,%g) = %0.10g\n", x[0], x[1], minf);
}
nlopt_optimize will return a negative result code on failure, but this usually only happens if you pass invalid parameters, it runs out of memory, or something like that. (Actually, most of the other NLopt functions also return an error code that you can check if you are paranoid.) (However, if it returns the failure code NLOPT_ROUNDOFF_LIMITED, indicating a breakdown due to roundoff errors, the minimum found may still be useful and you may want to still use it.) Otherwise, we print out the minimum function value and the corresponding parameters x.
Finally, we should call nlopt_destroy to dispose of the nlopt_opt object when we are done with it:
nlopt_destroy(opt);
Assuming we save this in a file tutorial.c, we would compile and link (on Unix) with:
cc tutorial.c -o tutorial -lnlopt -lm
The result of running the program should then be something like:
found minimum at f(0.333334,0.296296) = 0.544330847
That is, it found the correct parameters to about 5 significant digits and the correct minimum function value to about 6 significant digits. (This is better than we specified; this often occurs because the local optimization routines usually try to be conservative in estimating the error.)
Number of evaluations
Let's modify our program to print out the number of function evaluations that were required to obtain this result. First, we'll change our objective function to:
int count = 0;
double myfunc(int n, const double *x, double *grad, void *my_func_data)
{
++count;
if (grad) {
grad[0] = 0.0;
grad[1] = 0.5 / sqrt(x[1]);
}
return sqrt(x[1]);
}
using a global variable count that is incremented for each function evaluation. (We could also pass a pointer to a counter variable as my_func_data, if we wanted to avoid global variables.) Then, adding a printf:
printf("found minimum after %d evaluations\n", count);
we obtain:
found minimum after 11 evaluations found minimum at f(0.333334,0.296296) = 0.544330847
For such a simple problem, a gradient-based local optimization algorithm like MMA can converge very quickly!
Switching to a derivative-free algorithm
We can also try a derivative-free algorithm. Looking at the NLopt Algorithms list, another algorithm in NLopt that handles nonlinear constraints is COBYLA, which is derivative-free. To use it, we just change NLOPT_LD_MMA ("LD" means local optimization, derivative/gradient-based) into NLOPT_LN_COBYLA ("LN" means local optimization, no derivatives), and obtain:
found minimum after 31 evaluations found minimum at f(0.333329,0.2962) = 0.544242301
In such a low-dimensional problem, derivative-free algorithms usually work quite well—in this case, it only triples the number of function evaluations. However, the comparison is not perfect because, for the same relative x tolerance of 10−4, COBYLA is a bit less conservative and only finds the solution to 3 significant digits.
To do a fairer comparison of the two algorithms, we could set the x tolerance to zero and ask how many function evaluations each one requires to get the correct answer to three decimal places. We can specify this by using the stopval termination criterion, which allows us to halt the process as soon as a feasible point attains an objective function value less than stopval. In this case, we would set stopval to 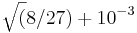 , replacing
, replacing nlopt_set_xtol_rel with the statement:
nlopt_set_stopval(opt, sqrt(8./27.)+1e-3);
corresponding to the last line of arguments to nlopt_minimize_constrained being sqrt(8./27.)+1e-3, 0.0, 0.0, 0.0, NULL, 0, 0.0. If we do this, we find that COBYLA requires 25 evaluations while MMA requires 10.
The advantage of gradient-based algorithms over derivative-free algorithms typically grows for higher-dimensional problems. On the other hand, derivative-free algorithms are much easier to use because you don't need to worry about how to compute the gradient (which might be tricky if the function is very complicated).
Example in C++
Although it is perfectly possible to use the C interface from C++, many C++ programmers will find it more natural to use real C++ objects instead of opaque nlopt_opt pointers, std::vector<double> instead of arrays, and exceptions instead of error codes. NLopt provides a C++ header file nlopt.hpp that you can use for this purpose, which simply wraps a C++ object interface around the C interface above.
#include <nlopt.hpp>
The equivalent of the above example would then be:
nlopt::opt opt(nlopt::LD_MMA, 2);
std::vector<double> lb(2);
lb[0] = -HUGE_VAL; lb[1] = 0;
opt.set_lower_bounds(lb);
opt.set_min_objective(myfunc, NULL);
my_constraint_data data[2] = { {2,0}, {-1,1} };
opt.add_inequality_constraint(myconstraint, &data[0], 1e-8);
opt.add_inequality_constraint(myconstraint, &data[1], 1e-8);
opt.set_xtol_rel(1e-4);
std::vector<double> x(2);
x[0] = 1.234; x[1] = 5.678;
double minf;
nlopt::result result = opt.optimize(x, minf);
There is no need to deallocate the opt object; its destructor will do that for you once it goes out of scope. Also, there is no longer any need to check for error codes; the NLopt C++ functions will throw exceptions if there is an error, which you can catch normally.
Here, we are using the same objective and constraint functions as in C, taking double* array arguments. Alternatively, you can define objective and constraint functions to take std::vector<double> arguments if you prefer. (Using std::vector<double> in the objective/constraint imposes a slight overhead because NLopt must copy the double* data to a std::vector<double>, but this overhead is unlikely to be significant in most real applications.) That is, you would do:
double myvfunc(const std::vector<double> &x, std::vector<double> &grad, void *my_func_data)
{
if (!grad.empty()) {
grad[0] = 0.0;
grad[1] = 0.5 / sqrt(x[1]);
}
return sqrt(x[1]);
}
double myvconstraint(const std::vector<double> &x, std::vector<double> &grad, void *data)
{
my_constraint_data *d = reinterpret_cast<my_constraint_data*>(data);
double a = d->a, b = d->b;
if (!grad.empty()) {
grad[0] = 3 * a * (a*x[0] + b) * (a*x[0] + b);
grad[1] = -1.0;
}
return ((a*x[0] + b) * (a*x[0] + b) * (a*x[0] + b) - x[1]);
}
Notice that, instead of checking whether grad is NULL, we check whether it is empty. (The vector arguments, if non-empty, are guaranteed to be of the same size as the dimension of the problem that you specified.) We then specify these in the same way as before:
opt.set_min_objective(myvfunc, NULL); opt.add_inequality_constraint(myvconstraint, &data[0], 1e-8); opt.add_inequality_constraint(myvconstraint, &data[1], 1e-8);
Note that the data pointers passed to these functions must remain valid (or rather, what they point to must remain valid) until you are done with opt. (It might have been nicer to use shared_ptr, but I don't like to rely on bleeding-edge language features.)
Instead of passing a separate data pointer, some users may wish to define a C++ function object class that contains all of the data needed by their function, with an overloaded operator() method to implement the function call. You can easily do this with a two-line helper function. If your function class is MyFunction, then you could define a static member function:
static double wrap(const std::vector<double> &x, std::vector<double> &grad, void *data) {
return (*reinterpret_cast<MyFunction*>(data))(x, grad); }
which you would then use e.g. by opt.set_min_objective(MyFunction::wrap, &some_MyFunction). Again, you have to make sure that some_MyFunction does not go out of scope before you are done calling nlopt::opt::optimize.
To link your program, just link to the C NLopt library (-lnlopt -lm on Unix).
Example in Matlab or GNU Octave
To implement this objective function in Matlab (or GNU Octave), we would write a file myfunc.m that looks like:
function [val, gradient] = myfunc(x)
val = sqrt(x(2));
if (nargout > 1)
gradient = [0, 0.5 / val];
end
Notice that we check the Matlab builtin variable nargout (the number of output arguments) to decide whether to compute the gradient. If we use a derivative-free optimization algorithm below, then nargout will always be 1 and the gradient need never be computed.
Our constraint function looks similar, except that it is parameterized by the coefficients a and b. We can just add these on as extra parameters, in a file myconstraint.m:
function [val, gradient] = myconstraint(x,a,b)
val = (a*x(1) + b)^3 - x(2);
if (nargout > 1)
gradient = [3*a*(a*x(1) + b)^2, -1];
end
The equivalent of the nlopt_opt is just a structure, with fields corresponding to any parameters that we want to set. (Any structure fields that we don't include are equivalent to not setting those parameters, and using the defaults instead). You can get more information on the available parameters by typing help nlopt_optimize in Matlab. The equivalent of the C example above is to define an opt structure by:
opt.algorithm = NLOPT_LD_MMA
opt.lower_bounds = [-inf, 0]
opt.min_objective = @myfunc
opt.fc = { (@(x) myconstraint(x,2,0)), (@(x) myconstraint(x,-1,1)) }
opt.fc_tol = [1e-8, 1e-8];
opt.xtol_rel = 1e-4
We do not need to specify the dimension of the problem; this is implicitly specified by the size of the initial-guess vector passed to nlopt_optimize below (and must match the sizes of other vectors like opt.lower_bounds). The inequality constraints are specified as a cell array opt.fc of function handles (and the corresponding tolerances are in an array opt.fc_tol); notice how we use @(x) to define an anonymous/inline function in order to pass additional arguments to myconstraint.
Finally, we call nlopt_optimize:
[xopt, fmin, retcode] = nlopt_optimize(opt, [1.234 5.678])
nlopt_optimize returns three things: xopt, the optimal parameters found; fmin, the corresponding value of the objective function, and a return code retcode (positive on success and negative on failure).
The output of the above command is:
xopt = 0.3333 0.2963 fmin = 0.5443 retcode = 4
(The return code 4 corresponds to NLOPT_XTOL_REACHED, which means it converged to the specified x tolerance.) To switch to a derivative-free algorithm like COBYLA, we just change opt.algorithm parameter:
opt.algorithm = NLOPT_LN_COBYLA
Matlab verbose output
It is often useful to print out some status message to see what is happening, especially if your function evaluation is much slower or if a large number of evaluations are required (e.g. for global optimization). You can, of course, modify your function to print out whatever you want. As a shortcut, however, you can set a verbose option in NLopt's Matlab interface by:
opt.verbose = 1;
If we do this, then running the MMA algorithm as above yields:
nlopt_minimize_constrained eval #1: 2.38286 nlopt_minimize_constrained eval #2: 2.35613 nlopt_minimize_constrained eval #3: 2.24586 nlopt_minimize_constrained eval #4: 2.0191 nlopt_minimize_constrained eval #5: 1.74093 nlopt_minimize_constrained eval #6: 1.40421 nlopt_minimize_constrained eval #7: 1.0223 nlopt_minimize_constrained eval #8: 0.685203 nlopt_minimize_constrained eval #9: 0.552985 nlopt_minimize_constrained eval #10: 0.544354 nlopt_minimize_constrained eval #11: 0.544331
This shows the objective function values at each intermediate step of the optimization. As in the C example above, it converges in 11 steps. The COBYLA algorithm requires a few more iterations, because it doesn't exploit the gradient information:
nlopt_optimize eval #1: 2.38286 nlopt_optimize eval #2: 2.38286 nlopt_optimize eval #3: 3.15222 nlopt_optimize eval #4: 1.20627 nlopt_optimize eval #5: 0.499441 nlopt_optimize eval #6: 0.709216 nlopt_optimize eval #7: 0.20341 nlopt_optimize eval #8: 0.745201 nlopt_optimize eval #9: 0.989693 nlopt_optimize eval #10: 0.324679 nlopt_optimize eval #11: 0.804318 nlopt_optimize eval #12: 0.541431 nlopt_optimize eval #13: 0.561137 nlopt_optimize eval #14: 0.531346 nlopt_optimize eval #15: 0.515784 nlopt_optimize eval #16: 0.541724 nlopt_optimize eval #17: 0.541422 nlopt_optimize eval #18: 0.541504 nlopt_optimize eval #19: 0.541499 nlopt_optimize eval #20: 0.541514 nlopt_optimize eval #21: 0.541352 nlopt_optimize eval #22: 0.542089 nlopt_optimize eval #23: 0.542575 nlopt_optimize eval #24: 0.543027 nlopt_optimize eval #25: 0.544911 nlopt_optimize eval #26: 0.541793 nlopt_optimize eval #27: 0.545225 nlopt_optimize eval #28: 0.544331 nlopt_optimize eval #29: 0.544256 nlopt_optimize eval #30: 0.544242 nlopt_optimize eval #31: 0.544116
Notice that some of the objective function values are below the minimum of 0.54433 — these are simply values of the objective function at infeasible points (violating the nonlinear constraints).
Example in Python
The same example in Python is:
import nlopt
from numpy import *
def myfunc(x, grad):
if grad.size > 0:
grad[0] = 0.0
grad[1] = 0.5 / sqrt(x[1])
return sqrt(x[1])
def myconstraint(x, grad, a, b):
if grad.size > 0:
grad[0] = 3 * a * (a*x[0] + b)**2
grad[1] = -1.0
return (a*x[0] + b)**3 - x[1]
opt = nlopt.opt(nlopt.LD_MMA, 2)
opt.set_lower_bounds([-float('inf'), 0])
opt.set_min_objective(myfunc)
opt.add_inequality_constraint(lambda x,grad: myconstraint(x,grad,2,0), 1e-8)
opt.add_inequality_constraint(lambda x,grad: myconstraint(x,grad,-1,1), 1e-8)
opt.set_xtol_rel(1e-4)
x = opt.optimize([1.234, 5.678])
minf = opt.last_optimum_value()
print "optimum at ", x[0],x[1]
print "minimum value = ", minf
print "result code = ", opt.last_optimize_result()
Notice that the optimize method returns only the location of the optimum (as a NumPy array), and that the value of the optimum and the result code are obtained by last_optimum_value and last_optimize_result values. Like in C++, the NLopt functions raise exceptions on errors, so we don't need to check return codes to look for errors.
The objective and constraint functions take NumPy arrays as arguments; if the grad argument is non-empty it must be modified in-place to the value of the gradient. Notice how we use Python's lambda construct to pass additional parameters to the constraints. Alternatively, we could define the objective/constraints as classes with a __call__(self, x, grad) method so that they can behave like functions.
The result of running the above code should be:
optimum at 0.333333331366 0.296296292697 minimum value = 0.544331050646 result = 4
finding the same correct optimum as in the C interface (of course). (The return code 4 corresponds to nlopt.XTOL_REACHED, which means it converged to the specified x tolerance.)
Important: Modifying grad in-place
The grad argument of your objective/constraint functions must be modified in-place. If you use an operation like
grad = 2*x
however, Python allocates a new array to hold 2*x and reassigns grad to point to it, rather than modifying the original contents of grad. This will not work. Instead, you should do:
grad[:] = 2*x
which overwrites the old contents of grad with 2*x. See also the NLopt Python Reference.
Example in GNU Guile (Scheme)
In GNU Guile, which is an implementation of the Scheme programming language, the equivalent of the example above would be:
(use-modules (nlopt))
(define (myfunc x grad)
(if grad
(begin
(vector-set! grad 0 0.0)
(vector-set! grad 1 (/ 0.5 (sqrt (vector-ref x 1))))))
(sqrt (vector-ref x 1)))
(define (myconstraint x grad a b)
(let ((x0 (vector-ref x 0)) (x1 (vector-ref x 1)))
(if grad
(begin
(vector-set! grad 0 (* 3 a (expt (+ (* a x0) b) 2)))
(vector-set! grad 1 -1.0)))
(- (expt (+ (* a x0) b) 3) x1)))
(define opt (new-nlopt-opt NLOPT-LD-MMA 2))
(nlopt-opt-set-lower-bounds opt (vector (- (inf)) 0))
(nlopt-opt-set-min-objective opt myfunc)
(nlopt-opt-add-inequality-constraint opt (lambda (x grad)
(myconstraint x grad 2 0))
1e-8)
(nlopt-opt-add-inequality-constraint opt (lambda (x grad)
(myconstraint x grad -1 1))
1e-8)
(nlopt-opt-set-xtol-rel opt 1e-4)
(define x (nlopt-opt-optimize opt (vector 1.234 5.678)))
(define minf (nlopt-opt-last-optimum-value opt))
(define result (nlopt-opt-last-optimize-result opt))
Note that the objective/constraint functions take two arguments, x and grad, and return a number. x is a vector whose length is the dimension of the problem; grad is either false (#f) if it is not needed, or a vector that must be modified in-place to the gradient of the function.
On error conditions, the NLopt functions throw exceptions that can be caught by your Scheme code if you wish.
The heavy use of side-effects here is a bit unnatural in Scheme, but is used in order to closely map to the C++ interface. (Notice that nlopt:: C++ functions map to nlopt- Guile functions, and nlopt::opt:: methods map to nlopt-opt- functions that take the opt object as the first argument.) Of course, you are free to wrap your own Scheme-like functional interface around this if you wish.
Example in Fortran
In Fortran, the equivalent of the C example above would be as follows. First, we would write our functions as:
subroutine myfunc(val, n, x, grad, need_gradient, f_data)
double precision val, x(n), grad(n)
integer n, need_gradient
if (need_gradient.ne.0) then
grad(1) = 0.0
grad(2) = 0.5 / dsqrt(x(2))
endif
val = dsqrt(x(2))
end
subroutine myconstraint(val, n, x, grad, need_gradient, d)
integer need_gradient
double precision val, x(n), grad(n), d(2), a, b
a = d(1)
b = d(2)
if (need_gradient.ne.0) then
grad(1) = 3. * a * (a*x(1) + b)**2
grad(2) = -1.0
endif
val = (a*x(1) + b)**3 - x(2)
end
Notice that that the "functions" are actually subroutines. This is because it turns out to be hard to call Fortran functions from C or vice versa in any remotely portable way. Therefore:
- In the NLopt Fortran interface, all C functions become subroutines in Fortran, with the return value becoming the first argument.
So, here the first argument val is used for the return value. Also, because there is no way in Fortran to pass NULL for the grad argument, we add an additional need_gradient argument which is nonzero if the gradient needs to be computed. Finally, the last argument is the equivalent of the void* argument in the C API, and can be used to pass a single argument of any type through to the objective/constraint functions: here, we use it in myconstraint to pass an array of two values for the constants a and b.
Then, to run the optimization, we can use the following Fortran program:
program main
external myfunc, myconstraint
double precision lb(2)
integer*8 opt
double precision d1(2), d2(2)
double precision x(2), minf
integer ires
include 'nlopt.f'
call nlo_create(opt, NLOPT_LD_MMA, 2)
call nlo_get_lower_bounds(ires, opt, lb)
lb(2) = 0.0
call nlo_set_lower_bounds(ires, opt, lb)
call nlo_set_min_objective(ires, opt, myfunc, 0)
d1(1) = 2.
d1(2) = 0.
call nlo_add_inequality_constraint(ires, opt,
$ myconstraint, d1, 1.D-8)
d2(1) = -1.
d2(2) = 1.
call nlo_add_inequality_constraint(ires, opt,
$ myconstraint, d2, 1.D-8)
call nlo_set_xtol_rel(ires, opt, 1.D-4)
x(1) = 1.234
x(2) = 5.678
call nlo_optimize(ires, opt, x, minf)
if (res.lt.0) then
write(*,*) 'nlopt failed!'
else
write(*,*) 'found min at ', x(1), x(2)
write(*,*) 'min val = ', minf
endif
call nlo_destroy(opt)
end
There are a few things to note here:
- All
nlopt_functions are converted intonlo_subroutines, with return values converted into the first argument. - The "
nlopt_opt" variableoptis declared asinteger*8. (Technically, we could use any type that is big enough to hold a pointer on all platforms;integer*8is big enough for pointers on both 32-bit and 64-bit machines.) - The subroutines must be declared as
external. - We
include 'nlopt.f'in order to get the various constants likeNLOPT_LD_MMA.
There is no standard Fortran 77 equivalent of C's HUGE_VAL constant, so instead we just call nlo_get_lower_bounds to get the default lower bounds (-∞) and then change one of them. In Fortran 90 (and supported as an extension in many Fortran 77 compilers), there is a huge intrinsic function that we could have used instead:
lb(1) = -huge(lb(1))