NLopt Reference
From AbInitio
| Revision as of 20:41, 20 July 2012 (edit) Stevenj (Talk | contribs) (→Vector storage for limited-memory quasi-Newton algorithms) ← Previous diff |
Revision as of 20:46, 20 July 2012 (edit) Stevenj (Talk | contribs) (→Preconditioning with approximate Hessians) Next diff → |
||
| Line 317: | Line 317: | ||
| If you know the Hessian (second-derivative) matrix of your objective function, i.e. the matrix ''H'' with <math>H_{ij} = \frac{\partial^2 f}{\partial x_i \partial x_j}</math> for an objective ''f'', then in principle this could be used to accelerate local optimization. In fact, even a reasonable ''approximation'' for ''H'' could be useful if it captures information about the largest eigenvalues of ''H'' and the corresponding eigenvectors. Such an approximate Hessian is often called a ''preconditioner'' in the context of iterative solvers, so we adopt that terminology here. | If you know the Hessian (second-derivative) matrix of your objective function, i.e. the matrix ''H'' with <math>H_{ij} = \frac{\partial^2 f}{\partial x_i \partial x_j}</math> for an objective ''f'', then in principle this could be used to accelerate local optimization. In fact, even a reasonable ''approximation'' for ''H'' could be useful if it captures information about the largest eigenvalues of ''H'' and the corresponding eigenvectors. Such an approximate Hessian is often called a ''preconditioner'' in the context of iterative solvers, so we adopt that terminology here. | ||
| - | T | + | Currently, support for preconditioners in NLopt is somewhat experimental, and is only used in the <code>NLOPT_LD_CCSAQ</code> algorithm. You specify a preconditioned objective function by calling one of: |
| + | |||
| + | nlopt_result nlopt_set_precond_min_objective(nlopt_opt opt, nlopt_func f, nlopt_precond pre, void *f_data); | ||
| + | nlopt_result nlopt_set_precond_min_objective(nlopt_opt opt, nlopt_func f, nlopt_precond pre, void *f_data); | ||
| + | |||
| + | which are identical to <code>nlopt_set_min_objective</code> and <code>nlopt_set_max_objective</code>, respectively, except that they additionally specify a preconditioner <code>pre</code>, which is a function of the form: | ||
| + | |||
| + | void pre(unsigned n, const double *x, const double *v, double *vpre, void *f_data); | ||
| + | |||
| + | This function takes a vector ''v'' and should compute ''vpre = H(x) v'' where ''H'' is an approximate second derivative at ''x''. The CCSAQ algorithm '''requires''' that your matrix ''H'' be [[w:Positive-definite_matrix#Positive-semidefinite|positive semidefinite]], i.e. that it be real-symmetric with nonnegative eigenvalues. | ||
| ==Version number== | ==Version number== | ||
Revision as of 20:46, 20 July 2012
| NLopt |
| Download |
| Release notes |
| FAQ |
| NLopt manual |
| Introduction |
| Installation |
| Tutorial |
| Reference |
| Algorithms |
| License and Copyright |
NLopt is a library, not a stand-alone program—it is designed to be called from your own program in C, C++, Fortran, Matlab, GNU Octave, or other languages. This reference section describes the programming interface (API) of NLopt in the C language. The reference manuals for other languages can be found at:
- NLopt C++ Reference
- NLopt Fortran Reference
- NLopt Matlab Reference
- NLopt Python Reference
- NLopt Guile Reference
The old API from versions of NLopt prior to 2.0 is deprecated, but continues to be supported for backwards compatibility. You can find it described in the NLopt Deprecated API Reference.
Other sources of information include the Unix man page: On Unix, you can run e.g. man nlopt for documentation of C API. In Matlab and GNU Octave, the corresponding command is to type help nlopt_optimize.
Compiling and linking your program to NLopt
An NLopt program in C should include the NLopt header file:
#include <nlopt.h>
For programs in compiled languages like C or Fortran, when you compile your program you will have to link it to the NLopt library. This is in addition to including the header file (#include <nlopt.h> in C or #include <nlopt.hpp> in C++). On Unix, you would normally link with a command something like:
compiler ...source/object files... -lnlopt -lm -o myprogram
where compiler is cc, f77, g++, or whatever is appropriate for your machine/language.
Note: the -lnlopt -lm options, which link to the NLopt library (and the math library, which it requires), must come after your source/object files. In general, the rule is that if A depends upon B, then A must come before B in the link command.
Note: the above example assumes that you have installed the NLopt library in a place where the compiler knows to find it (e.g. in a standard directory like /usr/lib or /usr/local/lib). If you installed somewhere else (e.g. in your home directory if you are not a system administrator), then you will need to use a -L flag to tell the compiler where to find the library. See the installation manual.
The nlopt_opt object
The NLopt API revolves around an "object" of type nlopt_opt (an opaque pointer type). Via this object, all of the parameters of the optimization are specified (dimensions, algorithm, stopping criteria, constraints, objective function, etcetera), and then one finally passes this object to nlopt_optimize in order to perform the optimization. The object is created by calling:
nlopt_opt nlopt_create(nlopt_algorithm algorithm, unsigned n);
which returns a newly allocated nlopt_opt object (or NULL if there was an error, e.g. out of memory), given an algorithm (see NLopt Algorithms for possible values) and the dimensionality of the problem (n, the number of optimization parameters).
When you are finished with the object, you must deallocate it by calling:
void nlopt_destroy(nlopt_opt opt);
Simple assignment (=) makes two pointers to the same object. To make an independent copy of an object, use:
nlopt_opt nlopt_copy(const nlopt_opt opt);
The algorithm and dimension parameters of the object are immutable (cannot be changed without creating a new object), but you can query them for a given object by calling:
nlopt_algorithm nlopt_get_algorithm(const nlopt_opt opt); unsigned nlopt_get_dimension(const nlopt_opt opt);
You can get a descriptive (null-terminated) string corresponding to a particular algorithm by calling:
const char *nlopt_algorithm_name(nlopt_algorithm algorithm);
Objective function
The objective function is specified by calling one of:
nlopt_result nlopt_set_min_objective(nlopt_opt opt, nlopt_func f, void* f_data); nlopt_result nlopt_set_max_objective(nlopt_opt opt, nlopt_func f, void* f_data);
depending on whether one wishes to minimize or maximize the objective function f, respectively. The function f should be of the form:
double f(unsigned n, const double* x, double* grad, void* f_data);
The return value should be the value of the function at the point x, where x points to an array of length n of the optimization parameters. The dimension n is identical to the one passed to nlopt_create.
In addition, if the argument grad is not NULL, then grad points to an array of length n which should (upon return) be set to the gradient of the function with respect to the optimization parameters at x. That is, grad[i] should upon return contain the partial derivative 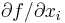 , for
, for 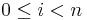 , if
, if grad is non-NULL. Not all of the optimization algorithms (below) use the gradient information: for algorithms listed as "derivative-free," the grad argument will always be NULL and need never be computed. (For algorithms that do use gradient information, however, grad may still be NULL for some calls.)
The f_data argument is the same as the one passed to nlopt_set_min_objective or nlopt_set_max_objective, and may be used to pass any additional data through to the function. (That is, it may be a pointer to some caller-defined data structure/type containing information your function needs, which you convert from void* by a typecast.)
Bound constraints
Most of the algorithms in NLopt are designed for minimization of functions with simple bound constraints on the inputs. That is, the input vectors x[i] are constrainted to lie in a hyperrectangle lb[i] ≤ x[i] ≤ ub[i] for 0 ≤ i < n. NLopt guarantees that your objective function and any nonlinear constraints will never be evaluated outside of these bounds (unlike nonlinear constraints, which may be violated at intermediate steps).
These bounds are specified by passing arrays lb and ub of length n (the dimension of the problem, from nlopt_create) to one or both of the functions:
nlopt_result nlopt_set_lower_bounds(nlopt_opt opt, const double* lb); nlopt_result nlopt_set_upper_bounds(nlopt_opt opt, const double* ub);
(Note that these functions make a copy of the lb and ub arrays, so subsequent changes to the caller's lb and ub arrays have no effect on the opt object.)
If a lower/upper bound is not set, the default is no bound (unconstrained, i.e. a bound of infinity); it is possible to have lower bounds but not upper bounds or vice versa. Alternatively, the user can call one of the above functions and explicitly pass a lower bound of -HUGE_VAL and/or an upper bound of +HUGE_VAL for some optimization parameters to make them have no lower/upper bound, respectively. (HUGE_VAL is the standard C constant for a floating-point infinity, found in the math.h header file.)
It is permitted to set lb[i] == ub[i] in one or more dimensions; this is equivalent to fixing the corresponding x[i] parameter, eliminating it from the optimization.
Note, however, that some of the algorithms in NLopt, in particular most of the global-optimization algorithms, do not support unconstrained optimization and will return an error in nlopt_optimize if you do not supply finite lower and upper bounds.
For convenience, the following two functions are supplied in order to set the lower/upper bounds for all optimization parameters to a single constant (so that you don’t have to fill an array with a constant value):
nlopt_result nlopt_set_lower_bounds1(nlopt_opt opt, double lb); nlopt_result nlopt_set_upper_bounds1(nlopt_opt opt, double ub);
The values of the lower and upper bounds can be retrieved by calling:
nlopt_result nlopt_get_lower_bounds(const nlopt_opt opt, double* lb); nlopt_result nlopt_get_upper_bounds(const nlopt_opt opt, double* ub);
where lb and ub are arrays of length n that, upon successful return, are set to copies of the lower and upper bounds, respectively.
Nonlinear constraints
Several of the algorithms in NLopt (MMA, COBYLA, and ORIG_DIRECT) also support arbitrary nonlinear inequality constraints, and some additionally allow nonlinear equality constraints (ISRES and AUGLAG). For these algorithms, you can specify as many nonlinear constraints as you wish by calling the following functions multiple times.
In particular, a nonlinear inequality constraint of the form fc(x) ≤ 0, where the function fc is of the same form as the objective function described above, can be specified by calling:
nlopt_result nlopt_add_inequality_constraint(nlopt_opt opt, nlopt_func fc, void* fc_data, double tol);
Just as for the objective function, fc_data is a pointer to arbitrary user data that will be passed through to the fc function whenever it is called. The parameter tol is a tolerance that is used for the purpose of stopping criteria only: a point x is considered feasible for judging whether to stop the optimization if fc(x) ≤ tol. A tolerance of zero means that NLopt will try not to consider any x to be converged unless fc is strictly non-positive; generally, at least a small positive tolerance is advisable to reduce sensitivity to rounding errors.
(The return value is negative if there was an error, e.g. an invalid argument or an out-of-memory situation.)
Similarly, a nonlinear equality constraint of the form h(x) = 0, where the function h is of the same form as the objective function described above, can be specified by calling:
nlopt_result nlopt_add_equality_constraint(nlopt_opt opt, nlopt_func h, void* h_data, double tol);
Just as for the objective function, h_data is a pointer to arbitrary user data that will be passed through to the h function whenever it is called. The parameter tol is a tolerance that is used for the purpose of stopping criteria only: a point x is considered feasible for judging whether to stop the optimization if |h(x)| ≤ tol. For equality constraints, a small positive tolerance is strongly advised in order to allow NLopt to converge even if the equality constraint is slightly nonzero.
(For any algorithm listed as "derivative-free" below, the grad argument to fc or h will always be NULL and need never be computed.)
To remove all of the inequality and/or equality constraints from a given problem opt, you can call the following functions:
nlopt_result nlopt_remove_inequality_constraints(nlopt_opt opt); nlopt_result nlopt_remove_equality_constraints(nlopt_opt opt);
Vector-valued constraints
In some applications with multiple constraints, it is more convenient to define a single function that returns the values (and gradients) of all constraints at once. For example, different constraint functions might share computations in some way. Or, if you have a large number of constraints, you may wish to compute them in parallel. This possibility is supported by the following function, which defines multiple constraints at once, or equivalently a vector-valued constraint function 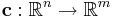 :
:
nlopt_result nlopt_add_inequality_mconstraint(nlopt_opt opt, unsigned m,
nlopt_mfunc c, void* c_data, const double *tol);
nlopt_result nlopt_add_equality_mconstraint(nlopt_opt opt, unsigned m,
nlopt_mfunc c, void* c_data, const double *tol);
Here, m is the dimensionality of the constraint result and tol points to an array of length m of the tolerances in each constraint dimension (or NULL for zero tolerances). The constraint function must be of the form:
void c(unsigned m, double *result, unsigned n, const double* x, double* grad, void* f_data);
This evaluates the constraint function(s) 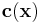 at the point
at the point x, an array of length n (the same as the dimension passed to nlopt_create). Upon return, the output value of the constraints should be stored in result, an array of length m (the same as the dimension passed to nlopt_add_*_mconstraint), so that result[i] stores ci.
In addition, if grad is non-NULL, then grad points to an array of length m*n which should, upon return, be set to the gradients of the constraint functions with respect to x. The n dimension of grad is stored contiguously, so that 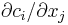 is stored in
is stored in grad[i*n + j].
An inequality constraint corresponds to 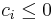 for
for 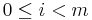 , and an equality constraint corresponds to ci = 0, in both cases with tolerance
, and an equality constraint corresponds to ci = 0, in both cases with tolerance tol[i] for purposes of termination criteria.
(You can add multiple vector-valued constraints and/or scalar constraints in the same problem.)
Stopping criteria
Multiple stopping criteria for the optimization are supported (see also the Introduction), as specified by the functions to modify a given optimization problem opt. The optimization halts whenever any one of these criteria is satisfied. In some cases, the precise interpretation of the stopping criterion depends on the optimization algorithm above (although we have tried to make them as consistent as reasonably possible), and some algorithms do not support all of the stopping criteria.
Note: you do not need to use all of the stopping criteria! In most cases, you only need one or two, and can omit the remainder (all criteria are disabled by default).
For each stopping criteria, there are (at least) two functions: a set function to specify the stopping criterion, and a get function to retrieve the current value for that criterion.
nlopt_result nlopt_set_stopval(nlopt_opt opt, double stopval); double nlopt_get_stopval(const nlopt_opt opt);
Stop when an objective value of at least stopval is found: stop minimizing when an objective value ≤ stopval is found, or stop maximizing a value ≥ stopval is found. (Setting stopval to -HUGE_VAL for minimizing or +HUGE_VAL for maximizing disables this stopping criterion.)
nlopt_result nlopt_set_ftol_rel(nlopt_opt opt, double tol); double nlopt_get_ftol_rel(const nlopt_opt opt);
Set relative tolerance on function value: stop when an optimization step (or an estimate of the optimum) changes the objective function value by less than tol multiplied by the absolute value of the function value. (If there is any chance that your optimum function value is close to zero, you might want to set an absolute tolerance with nlopt_set_ftol_abs as well.) Criterion is disabled if tol is non-positive.
nlopt_result nlopt_set_ftol_abs(nlopt_opt opt, double tol); double nlopt_get_ftol_abs(const nlopt_opt opt);
Set absolute tolerance on function value: stop when an optimization step (or an estimate of the optimum) changes the function value by less than tol. Criterion is disabled if tol is non-positive.
nlopt_result nlopt_set_xtol_rel(nlopt_opt opt, double tol); double nlopt_get_xtol_rel(const nlopt_opt opt);
Set relative tolerance on optimization parameters: stop when an optimization step (or an estimate of the optimum) changes every parameter by less than tol multiplied by the absolute value of the parameter. (If there is any chance that an optimal parameter is close to zero, you might want to set an absolute tolerance with nlopt_set_xtol_abs as well.) Criterion is disabled if tol is non-positive.
nlopt_result nlopt_set_xtol_abs(nlopt_opt opt, const double* tol); nlopt_result nlopt_get_xtol_abs(const nlopt_opt opt, double *tol);
Set absolute tolerances on optimization parameters. tol is a pointer to an array of length n (the dimension from nlopt_create) giving the tolerances: stop when an optimization step (or an estimate of the optimum) changes every parameter x[i] by less than tol[i]. (Note that this function makes a copy of the tol array, so subsequent changes to the caller's tol have no effect on opt.) In nlopt_get_xtol_abs, tol must be an array of length n, which upon successful return contains a copy of the current tolerances.
For convenience, the following function may be used to set the absolute tolerances in all n optimization parameters to the same value:
nlopt_result nlopt_set_xtol_abs1(nlopt_opt opt, double tol);
Criterion is disabled if tol is non-positive.
nlopt_result nlopt_set_maxeval(nlopt_opt opt, int maxeval); int nlopt_get_maxeval(nlopt_opt opt);
Stop when the number of function evaluations exceeds maxeval. (This is not a strict maximum: the number of function evaluations may exceed maxeval slightly, depending upon the algorithm.) Criterion is disabled if maxeval is non-positive.
nlopt_result nlopt_set_maxtime(nlopt_opt opt, double maxtime); double nlopt_get_maxtime(nlopt_opt opt);
Stop when the optimization time (in seconds) exceeds maxtime. (This is not a strict maximum: the time may exceed maxtime slightly, depending upon the algorithm and on how slow your function evaluation is.) Criterion is disabled if maxtime is non-positive.
Forced termination
In certain cases, the caller may wish to force the optimization to halt, for some reason unknown to NLopt. For example, if the user presses Ctrl-C, or there is an error of some sort in the objective function. (This is used to implement exception handling in the NLopt wrappers for C++ and other languages.) In this case, it is possible to tell NLopt to halt the optimization gracefully, returning the best point found so far, by calling the following function from within your objective or constraint functions:
nlopt_result nlopt_force_stop(nlopt_opt opt);
This causes nlopt_optimize to halt, returning the NLOPT_FORCED_STOP error code (below). It has no effect if not called during nlopt_optimize.
If you want to provide a bit more information, you can call
nlopt_result nlopt_set_force_stop(nlopt_opt opt, int val)
to set a forced-stop integer value val, which can be later retrieved by calling:
int nlopt_get_force_stop(nlopt_opt opt)
which returns the last force-stop value that was set since the last nlopt_optimize. The force-stop value is reset to zero at the beginning of nlopt_optimize. Passing val=0 to nlopt_set_force_stop tells NLopt not to force a halt.
Performing the optimization
Once all of the desired optimization parameters have been specified in a given object opt, you can perform the optimization by calling:
nlopt_result nlopt_optimize(nlopt_opt opt, double *x, double *opt_f);
On input, x is an array of length n (the dimension of the problem from nlopt_create) giving an initial guess for the optimization parameters. On successful return, x contains the optimized values of the parameters, and opt_f contains the corresponding value of the objective function.
The return value (see below) is positive on success and negative on failure.
Return values
Most of the NLopt functions return an enumerated constant of type nlopt_result, which takes on one of the following values:
Successful termination (positive return values)
NLOPT_SUCCESS = 1- Generic success return value.
NLOPT_STOPVAL_REACHED = 2- Optimization stopped because
stopval(above) was reached. NLOPT_FTOL_REACHED = 3- Optimization stopped because
ftol_relorftol_abs(above) was reached. NLOPT_XTOL_REACHED = 4- Optimization stopped because
xtol_relorxtol_abs(above) was reached. NLOPT_MAXEVAL_REACHED = 5- Optimization stopped because
maxeval(above) was reached. NLOPT_MAXTIME_REACHED = 6- Optimization stopped because
maxtime(above) was reached.
Error codes (negative return values)
NLOPT_FAILURE = -1- Generic failure code.
NLOPT_INVALID_ARGS = -2- Invalid arguments (e.g. lower bounds are bigger than upper bounds, an unknown algorithm was specified, etcetera).
NLOPT_OUT_OF_MEMORY = -3- Ran out of memory.
NLOPT_ROUNDOFF_LIMITED = -4- Halted because roundoff errors limited progress. (In this case, the optimization still typically returns a useful result.)
NLOPT_FORCED_STOP = -5- Halted because of a forced termination: the user called
nlopt_force_stop(opt)on the optimization’snlopt_optobjectoptfrom the user’s objective function or constraints.
Local/subsidiary optimization algorithm
Some of the algorithms, especially MLSL and AUGLAG, use a different optimization algorithm as a subroutine, typically for local optimization. You can change the local search algorithm and its tolerances by calling:
nlopt_result nlopt_set_local_optimizer(nlopt_opt opt, const nlopt_opt local_opt);
Here, local_opt is another nlopt_opt object whose parameters are used to determine the local search algorithm, its stopping criteria, and other algorithm parameters. (However, the objective function, bounds, and nonlinear-constraint parameters of local_opt are ignored.) The dimension n of local_opt must match that of opt.
This function makes a copy of the local_opt object, so you can freely destroy your original local_opt afterwards.
Initial step size
For derivative-free local-optimization algorithms, the optimizer must somehow decide on some initial step size to perturb x by when it begins the optimization. This step size should be big enough that the value of the objective changes significantly, but not too big if you want to find the local optimum nearest to x. By default, NLopt chooses this initial step size heuristically from the bounds, tolerances, and other information, but this may not always be the best choice.
You can modify the initial step size by calling:
nlopt_result nlopt_set_initial_step(nlopt_opt opt, const double* dx);
Here, dx is an array of length n (the dimension of the problem from nlopt_create) containing the (nonzero) initial step size for each component of the optimization parameters x. If you pass NULL for dx, then NLopt will use its heuristics to determine the initial step size. For convenience, if you want to set the step sizes in every direction to be the same value, you can instead call:
nlopt_result nlopt_set_initial_step1(nlopt_opt opt, double dx);
You can get the initial step size by calling:
nlopt_result nlopt_get_initial_step(const nlopt_opt opt, const double *x, double *dx);
Here, x is the same as the initial guess that you plan to pass to nlopt_optimize – if you have not set the initial step and NLopt is using its heuristics, its heuristic step size may depend on the initial x, which is why you must pass it here. Both x and dx are arrays of length n (the dimension of the problem from nlopt_create), where dx on successful return contains the initial step sizes.
Stochastic population
Several of the stochastic search algorithms (e.g., CRS, MLSL, and ISRES) start by generating some initial "population" of random points x. By default, this initial population size is chosen heuristically in some algorithm-specific way, but the initial population can by changed by calling:
nlopt_result nlopt_set_population(nlopt_opt opt, unsigned pop);
(A pop of zero implies that the heuristic default will be used.)
Pseudorandom numbers
For stochastic optimization algorithms, we use pseudorandom numbers generated by the Mersenne Twister algorithm, based on code from Makoto Matsumoto. By default, the seed for the random numbers is generated from the system time, so that you will get a different sequence of pseudorandom numbers each time you run your program. If you want to use a "deterministic" sequence of pseudorandom numbers, i.e. the same sequence from run to run, you can set the seed by calling:
void nlopt_srand(unsigned long seed);
Some of the algorithms also support using low-discrepancy sequences (LDS), sometimes known as quasi-random numbers. NLopt uses the Sobol LDS, which is implemented for up to 1111 dimensions.
To reset the seed based on the system time, you can call:
void nlopt_srand_time(void);
(Normally, you don't need to call this as it is called automatically. However, it might be useful if you want to "re-randomize" the pseudorandom numbers after calling nlopt_srand to set a deterministic seed.)
Vector storage for limited-memory quasi-Newton algorithms
Some of the NLopt algorithms are limited-memory "quasi-Newton" algorithms, which "remember" the gradients from a finite number M of the previous optimization steps in order to construct an approximate 2nd derivative matrix. The bigger M is, the more storage the algorithms require, but on the other hand they may converge faster for larger M. By default, NLopt chooses a heuristic value of M, but this can be changed/retrieved by calling:
nlopt_result nlopt_set_vector_storage(nlopt_opt opt, unsigned M); unsigned nlopt_get_vector_storage(const nlopt_opt opt);
Passing M=0 (the default) tells NLopt to use a heuristic value. By default, NLopt currently sets M to 10 or at most 10 MiB worth of vectors, whichever is larger.
Preconditioning with approximate Hessians
If you know the Hessian (second-derivative) matrix of your objective function, i.e. the matrix H with 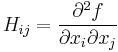 for an objective f, then in principle this could be used to accelerate local optimization. In fact, even a reasonable approximation for H could be useful if it captures information about the largest eigenvalues of H and the corresponding eigenvectors. Such an approximate Hessian is often called a preconditioner in the context of iterative solvers, so we adopt that terminology here.
for an objective f, then in principle this could be used to accelerate local optimization. In fact, even a reasonable approximation for H could be useful if it captures information about the largest eigenvalues of H and the corresponding eigenvectors. Such an approximate Hessian is often called a preconditioner in the context of iterative solvers, so we adopt that terminology here.
Currently, support for preconditioners in NLopt is somewhat experimental, and is only used in the NLOPT_LD_CCSAQ algorithm. You specify a preconditioned objective function by calling one of:
nlopt_result nlopt_set_precond_min_objective(nlopt_opt opt, nlopt_func f, nlopt_precond pre, void *f_data); nlopt_result nlopt_set_precond_min_objective(nlopt_opt opt, nlopt_func f, nlopt_precond pre, void *f_data);
which are identical to nlopt_set_min_objective and nlopt_set_max_objective, respectively, except that they additionally specify a preconditioner pre, which is a function of the form:
void pre(unsigned n, const double *x, const double *v, double *vpre, void *f_data);
This function takes a vector v and should compute vpre = H(x) v where H is an approximate second derivative at x. The CCSAQ algorithm requires that your matrix H be positive semidefinite, i.e. that it be real-symmetric with nonnegative eigenvalues.
Version number
To determine the version number of NLopt at runtime, you can call:
void nlopt_version(int *major, int *minor, int *bugfix);
For example, NLopt version 3.1.4 would return *major=3, *minor=1, and *bugfix=4.