NLopt Python Reference
From AbInitio
(diff) ←Older revision | Current revision | Newer revision→ (diff)
| NLopt |
| Download |
| Release notes |
| FAQ |
| NLopt manual |
| Introduction |
| Installation |
| Tutorial |
| Reference |
| Algorithms |
| License and Copyright |
The NLopt includes an interface callable from the Python programming language.
The main purpose of this section is to document the syntax and unique features of the Python API; for more detail on the underlying features, please refer to the C documentation in the NLopt Reference.
Using the NLopt Python API
To use NLopt in Python, your Python program should include the lines:
import nlopt from numpy import *
which imports the nlopt module, and also imports the numpy (NumPy) that defines the array data types used for communicating with NLopt.
The nlopt.opt class
The NLopt API revolves around an object of type nlopt.opt. Via methods of this object, all of the parameters of the optimization are specified (dimensions, algorithm, stopping criteria, constraints, objective function, etcetera), and then one finally calls the opt.optimize method in order to perform the optimization. The object should normally be created via the constructor:
opt = nlopt.opt(algorithm, n)
given an algorithm (see NLopt Algorithms for possible values) and the dimensionality of the problem (n, the number of optimization parameters). Whereas the C algorithms are specified by nlopt_algorithm constants of the form NLOPT_LD_MMA, NLOPT_LN_COBYLA, etcetera, the Python algorithm values are of the form nlopt.LD_MMA, nlopt.LN_COBYLA, etcetera (with the NLOPT_ prefix replaced by the nlopt. namespace).
There are also a copy constructor nlopt.opt(opt) to make a copy of a given object (equivalent to nlopt_copy in the C API).
If there is an error in the constructor (or copy constructor, or assignment), a MemoryError exception is thrown.
The algorithm and dimension parameters of the object are immutable (cannot be changed without constructing a new object), but you can query them for a given object by the methods:
opt.get_algorithm() opt.get_dimension()
You can get a string description of the algorithm via:
opt.get_algorithm_name()
Objective function
The objective function is specified by calling one of the methods:
opt.set_min_objective(f) opt.set_max_objective(f)
depending on whether one wishes to minimize or maximize the objective function f, respectively. The function f should be of the form:
def f(x, grad):
if grad.size > 0:
...set grad to gradient, in-place...
return ...value of f(x)...
The return value should be the value of the function at the point x, where x is a NumPy array of length n of the optimization parameters (the same as the dimension passed to the constructor).
In addition, if the argument grad is not empty [i.e. grad.size>0], then grad is a NumPy array of length n which should (upon return) be set to the gradient of the function with respect to the optimization parameters at x. That is, grad[i] should upon return contain the partial derivative 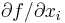 , for
, for 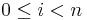 , if
, if grad is non-empty. Not all of the optimization algorithms (below) use the gradient information: for algorithms listed as "derivative-free," the grad argument will always be empty and need never be computed. (For algorithms that do use gradient information, however, grad may still be empty for some calls.)
Note that grad must be modified in-place by your function f. Generally, this means using indexing operations grad[...] = ... to overwrite the contents of grad, as described below.
Assigning results in-place
Your objective and constraint functions must overwrite the contents of the grad (gradient) argument in-place (although of course you can allocate whatever additional storage you might need, in addition to overwriting grad). However, typical Python assignment operations do not do this. For example:
grad = 2*x
might seem like the gradient of the function sum(x**2), but it will not work with NLopt because this expression actually allocates a new array to store 2*x and re-assigns grad to point to it, rather than overwriting the old contents of grad. Instead, you should do:
grad[:] = 2*x
Assigning any slice or view grad[...] of the array will overwrite the contents, which is what NLopt needs you to do. So, you should generally use indexing expressions grad[...] = ... to assign the gradient result.
In specific cases, there are a few other NumPy and SciPy functions that are documented to operate in-place on their arguments, and you can also use such functions to modify grad if you want. If a function is not explicitly documented to modify its arguments in-place, however, you should assume that it does not.
Bound constraints
The bound constraints can be specified by calling the methods:
opt.set_lower_bounds(lb) opt.set_upper_bounds(ub)
where lb and ub are arrays (NumPy arrays or Python lists) of length n (the same as the dimension passed to the nlopt.opt constructor). For convenience, these are overloaded with functions that take a single number as arguments, in order to set the lower/upper bounds for all optimization parameters to a single constant.
To retrieve the values of the lower/upper bounds, you can call one of:
opt.get_lower_bounds() opt.get_upper_bounds()
both of which return NumPy arrays.
To specify an unbounded dimension, you can use ±float('inf') (or ±numpy.inf) in Python to specify ±∞.
Nonlinear constraints
Just as for nonlinear constraints in C, you can specify nonlinear inequality and equality constraints by the methods:
opt.add_inequality_constraint(fc, tol=0) opt.add_equality_constraint(h, tol=0)
where the arguments fc and h have the same form as the objective function above. The optional tol arguments specify a tolerance in judging feasibility for the purposes of stopping the optimization, as in C.
To remove all of the inequality and/or equality constraints from a given problem, you can call the following methods:
opt.remove_inequality_constraints() opt.remove_equality_constraints()
Vector-valued constraints
Just as for nonlinear constraints in C, you can specify vector-valued nonlinear inequality and equality constraints by the methods
opt.add_inequality_mconstraint(c, tol) opt.add_inequality_mconstraint(c, tol)
Here, tol is an array (NumPy array or Python list) of the tolerances in each constraint dimension; the dimensionality m of the constraint is determined by tol.size. The constraint function c must be of the form:
def c(result, x, grad):
if grad.size > 0:
...set grad to gradient, in-place...
result[0] = ...value of c0(x)...
result[1] = ...value of c1(x)...
...
result is a NumPy array whose length equals the dimensionality m of the constraint (same as the length of tol above), which upon return should be set in-place (see above) to the constraint results at the point x (a NumPy array whose length n is the same as the dimension passed to the constructor). Any return value of the function is ignored.
In addition, if the argument grad is not empty [i.e. grad.size>0], then grad is a 2d NumPy array of size m×n which should (upon return) be set in-place (see above) to the gradient of the function with respect to the optimization parameters at x. That is, grad[i,j] should upon return contain the partial derivative 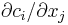 if
if grad is non-empty. Not all of the optimization algorithms (below) use the gradient information: for algorithms listed as "derivative-free," the grad argument will always be empty and need never be computed. (For algorithms that do use gradient information, however, grad may still be empty for some calls.)
An inequality constraint corresponds to 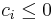 for
for 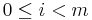 , and an equality constraint corresponds to ci = 0, in both cases with tolerance
, and an equality constraint corresponds to ci = 0, in both cases with tolerance tol[i] for purposes of termination criteria.
(You can add multiple vector-valued constraints and/or scalar constraints in the same problem.)
Stopping criteria
As explained in the C API Reference and the Introduction), you have multiple options for different stopping criteria that you can specify. (Unspecified stopping criteria are disabled; i.e., they have innocuous defaults.)
For each stopping criteria, there are (at least) two methods: a set method to specify the stopping criterion, and a get method to retrieve the current value for that criterion. The meanings of each criterion are exactly the same as in the C API.
opt.set_stopval(stopval) opt.get_stopval()
Stop when an objective value of at least stopval is found.
opt.set_ftol_rel(tol) opt.get_ftol_rel()
Set relative tolerance on function value.
opt.set_ftol_abs(tol) opt.get_ftol_abs()
Set absolute tolerance on function value.
opt.set_xtol_rel(tol) opt.get_xtol_rel()
Set relative tolerance on optimization parameters.
opt.set_xtol_abs(tol) opt.get_xtol_abs()
Set absolute tolerances on optimization parameters. The tol input must be an array (NumPy array or Python list) of length n (the dimension specified in the nlopt.opt constructor); alternatively, you can pass a single number in order to set the same tolerance for all optimization parameters. get_xtol_abs() returns the tolerances as a NumPy array.
opt.set_maxeval(maxeval) opt.get_maxeval()
Stop when the number of function evaluations exceeds maxeval. (0 or negative for no limit.)
opt.set_maxtime(maxtime) opt.get_maxtime()
Stop when the optimization time (in seconds) exceeds maxtime. (0 or negative for no limit.)
Forced termination
In certain cases, the caller may wish to force the optimization to halt, for some reason unknown to NLopt. For example, if the user presses Ctrl-C, or there is an error of some sort in the objective function. You can do this by raise any exception inside your objective/constraint functions:the optimization will be halted gracefully, and the same exception will be raised to the caller. See Exceptions, below. The Python equivalent of nlopt_forced_stop from the C API is to throw an nlopt.ForcedStop exception.
Performing the optimization
Once all of the desired optimization parameters have been specified in a given object opt, you can perform the optimization by calling:
xopt = opt.optimize(x)
On input, x is an array (NumPy array or Python list) of length n (the dimension of the problem from the nlopt.opt constructor) giving an initial guess for the optimization parameters. The return value xopt is a NumPy array containing the optimized values of the optimization parameters.
You can call the following methods to retrieve the optimized objective function value from the last optimize call, and also the return code (including negative/failure return values) from the last optimize call:
opt_val = opt.last_optimum_value() result = opt.last_optimize_result()
The return code (see below) is positive on success, indicating the reason for termination. On failure (negative return codes), optimize() throws an exception (see Exceptions, below).
Return values
The possible return values are the same as the return values in the C API, except that the NLOPT_ prefix is replaced with the nlopt. namespace. That is, NLOPT_SUCCESS becomes nlopt.SUCCESS, etcetera.
Exceptions
The Error codes (negative return values) in the C API are replaced in the Python API by thrown exceptions. The following exceptions are thrown by the various routines:
RunTimeError- Generic failure, equivalent to
NLOPT_FAILURE. ValueError- Invalid arguments (e.g. lower bounds are bigger than upper bounds, an unknown algorithm was specified, etcetera), equivalent to
NLOPT_INVALID_ARGS. MemoryError- Ran out of memory (a memory allocation failed), equivalent to
NLOPT_OUT_OF_MEMORY. nlopt.RoundoffLimited(subclass ofException)- Halted because roundoff errors limited progress, equivalent to
NLOPT_ROUNDOFF_LIMITED. nlopt.ForcedStop(subclass ofException)- Halted because of a forced termination: the user called
opt.force_stop()from the user’s objective function or threw annlopt.ForcedStopexception. Equivalent toNLOPT_FORCED_STOP.
If your objective/constraint functions throw any exception during the execution of opt.optimize, it will be caught by NLopt and the optimization will be halted gracefully, and opt.optimize will re-throw the same exception to its caller.
Local/subsidiary optimization algorithm
Some of the algorithms, especially MLSL and AUGLAG, use a different optimization algorithm as a subroutine, typically for local optimization. You can change the local search algorithm and its tolerances by calling:
opt.set_local_optimizer(local_opt)
Here, local_opt is another nlopt.opt object whose parameters are used to determine the local search algorithm, its stopping criteria, and other algorithm parameters. (However, the objective function, bounds, and nonlinear-constraint parameters of local_opt are ignored.) The dimension n of local_opt must match that of opt.
This function makes a copy of the local_opt object, so you can freely change your original local_opt afterwards without affecting opt.
Initial step size
Just as in the C API, you can get and set the initial step sizes for derivative-free optimization algorithms. The Python equivalents of the C functions are the following methods:
opt.set_initial_step(dx) opt.get_initial_step(x)
Here, dx is an array (NumPy array or Python list) of the (nonzero) initial steps for each dimension, or a single number if you wish to use the same initial steps for all dimensions. opt.get_initial_step(x) returns the initial step that will be used for a starting guess of x in opt.optimize(x).
Stochastic population
Just as in the C API, you can get and set the initial population for stochastic optimization algorithms, by the methods:
opt.set_population(pop) opt.get_population()
(A pop of zero implies that the heuristic default will be used.)
Pseudorandom numbers
For stochastic optimization algorithms, we use pseudorandom numbers generated by the Mersenne Twister algorithm, based on code from Makoto Matsumoto. By default, the seed for the random numbers is generated from the system time, so that you will get a different sequence of pseudorandom numbers each time you run your program. If you want to use a "deterministic" sequence of pseudorandom numbers, i.e. the same sequence from run to run, you can set the seed by calling:
nlopt.srand(seed)
where seed is an integer. To reset the seed based on the system time, you can call:
nlopt.srand_time()
(Normally, you don't need to call this as it is called automatically. However, it might be useful if you want to "re-randomize" the pseudorandom numbers after calling nlopt.srand to set a deterministic seed.)
Vector storage for limited-memory quasi-Newton algorithms
Just as in the C API, you can get and set the number M of stored vectors for limited-memory quasi-Newton algorithms, via the methods:
opt.set_vector_storage(M) opt.get_vector_storage()
(The default is M=0, in which case NLopt uses a heuristic nonzero value.)
Version number
To determine the version number of NLopt at runtime, you can call:
nlopt.version_major() nlopt.version_minor() nlopt.version_bugfix()
For example, NLopt version 3.1.4 would return major=3, minor=1, and bugfix=4.