NLopt Matlab Reference
From AbInitio
| Revision as of 18:28, 26 May 2011 (edit) Stevenj (Talk | contribs) (→Vector storage for limited-memory quasi-Newton methods) ← Previous diff |
Current revision (20:50, 20 July 2012) (edit) Stevenj (Talk | contribs) (→Objective function) |
||
| Line 36: | Line 36: | ||
| In addition, if the caller requests two return values (<code>nargout > 1</code>), then the second return value <code>gradient</code> should be a vector (row or column) of length <code>n</code> that is the gradient of the function with respect to the optimization parameters at <code>x</code>. That is, <code>grad(i)</code> should upon return contain the partial derivative <math>\partial f / \partial x_i</math>, for <math>1 < i \leq n</math>. Not all of the optimization algorithms (below) use the gradient information: for algorithms listed as "derivative-free," the <code>nargout</code> will always be 1 and the gradient need never be computed. | In addition, if the caller requests two return values (<code>nargout > 1</code>), then the second return value <code>gradient</code> should be a vector (row or column) of length <code>n</code> that is the gradient of the function with respect to the optimization parameters at <code>x</code>. That is, <code>grad(i)</code> should upon return contain the partial derivative <math>\partial f / \partial x_i</math>, for <math>1 < i \leq n</math>. Not all of the optimization algorithms (below) use the gradient information: for algorithms listed as "derivative-free," the <code>nargout</code> will always be 1 and the gradient need never be computed. | ||
| + | |||
| + | If your objective function returns [[w:NaN|NaN]] (<code>nan</code> in Matlab), that will force the optimization to terminate, equivalent to calling [[NLopt Reference#Forced termination|nlopt_force_stop]] in C. | ||
| ==Bound constraints== | ==Bound constraints== | ||
Current revision
| NLopt |
| Download |
| Release notes |
| FAQ |
| NLopt manual |
| Introduction |
| Installation |
| Tutorial |
| Reference |
| Algorithms |
| License and Copyright |
The NLopt includes interfaces callable from the Matlab and GNU Octave (a free-software Matlab-like program), using identical syntax.
The main purpose of this section is to document the syntax and unique features of the Matlab API; for more detail on the underlying features, please refer to the C documentation in the NLopt Reference.
Using the NLopt Matlab API
On Unix, the Matlab and Octave interfaces should automatically be installed in places where they will be found at runtime, assuming you have Matlab and Octave correctly installed on your machine, as documented in the Installation manual.
On Windows, we provide a precompiled .zip file of the NLopt library, which includes a matlab directory. In this directory are a set of .m files (mostly implementing constants and documentation) and a nlopt-optimize.c file which can be compiled into a w:MEX file callable from Matlab. All of these files must be placed somewhere in your Matlab path or in your working directory if you want to use them.
The opt structure
The NLopt API revolves around an Matlab structure, analogous to the nlopt_opt object in C and similar objects in NLopt's interfaces for other languages. All of the parameters of the optimization are specified (dimensions, algorithm, stopping criteria, constraints, objective function, etcetera) simply by assigning fields to this structure, and then one finally calls the nlopt_optimize(opt) function in order to perform the optimization. Every opt structure should specify the algorithm, via:
opt.algorithm = algorithm
given an algorithm (see NLopt Algorithms for possible values) and the dimensionality of the problem (n, the number of optimization parameters). Just as in C, algorithms are specified by predefined constants of the form NLOPT_MMA, NLOPT_COBYLA, etcetera.
You need not set all the fields of the structure; any fields that are not specified take on innocuous default values (the same as if you did not specify those parameters in the C interface).
The dimension n of the problem (the number of optimization parameters) is determined implicitly by the length of the vector you pass to nlopt_optimize as the initial guess. An error will occur if you use vectors of inconsistent lengths (e.g. you set opt.lower_bounds to be a different length).
Objective function
The objective function is specified setting either the opt.min_objective or opt.max_objective field to a function handle for the objective function f, depending on whether one wishes to minimize or maximize f, respectively. The function f should be of the form:
function [val, gradient] = myfunc(x)
val = ...value of f(x)...
if (nargout > 1)
gradient = ...gradient at x...
end
The first return value should be the value of the function at the point x, where x row or column vector of the n of the n optimization parameters (the same length as the initial guess passed to nlopt_optimize). (Whether x is a row or column vector depends on whether the initial guess you pass to nlopt_optimize is a row or column vector, respectively.)
In addition, if the caller requests two return values (nargout > 1), then the second return value gradient should be a vector (row or column) of length n that is the gradient of the function with respect to the optimization parameters at x. That is, grad(i) should upon return contain the partial derivative 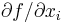 , for
, for 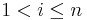 . Not all of the optimization algorithms (below) use the gradient information: for algorithms listed as "derivative-free," the
. Not all of the optimization algorithms (below) use the gradient information: for algorithms listed as "derivative-free," the nargout will always be 1 and the gradient need never be computed.
If your objective function returns NaN (nan in Matlab), that will force the optimization to terminate, equivalent to calling nlopt_force_stop in C.
Bound constraints
The bound constraints can be specified by setting opt.lower_bounds and/or opt.upper_bounds to vectors of length n (the same as the length of the initial guess passed to nlopt_optimize).
To specify an unbounded dimension, you can use ±inf in Matlab to specify ±∞.
Nonlinear constraints
Just as for nonlinear constraints in C, you can specify nonlinear inequality and equality constraints by setting opt.fc and opt.h to be cell arrays of function handles (of the same form as the objective function above) for the inequality and equality constraints, respectively.
Recall that a cell array is specified via {...} in Matlab, e.g. { @constraint1, @constraint2 }.
Optionally, you can specify a tolerance in judging feasibility for the purposes of stopping the optimization, as in C. Tolerances are specified as fields opt.fc_tol and opt.h_tol, which (if they are set) should be vectors (not cell arrays) of tolerances, of the same lengths as opt.fc and opt.h, respectively. (If they are not specified, the tolerances default to zero.)
Stopping criteria
As explained in the C API Reference and the Introduction), you have multiple options for different stopping criteria that you can specify. (Unspecified stopping criteria are disabled; i.e., they have innocuous defaults.) The various stopping criteria can be specified via the following fields of your structure.
opt.stopval
Stop when an objective value of at least stopval is found.
opt.ftol_rel
Set relative tolerance on function value.
opt.ftol_abs
Set absolute tolerance on function value.
opt.xtol_rel
Set relative tolerance on optimization parameters.
opt.xtol_abs
Set absolute tolerances on optimization parameters. The opt.xtol_abs value must be a vector of length n (the same length as the initial guess passed to nlopt_optimize) of the tolerances.
opt.maxeval
Stop when the number of function evaluations exceeds maxeval. (0 or negative for no limit.) An integer.
opt.maxtime
Stop when the optimization time (in seconds) exceeds maxtime. (0 or negative for no limit.)
Performing the optimization
Once all of the desired optimization parameters have been specified in a given structure opt, you can perform the optimization by calling:
[xopt, fmin, retcode] = nlopt_optimize(opt, x);
On input, x is a vector (row or column) of length n (this specifies the dimension of the problem, and must be consistent with vectors you use elsewhere as mentioned above) giving an initial guess for the optimization parameters. The return value xopt is a vector (row or column, same as x) containing the optimized values of the optimization parameters.
The second return value fmin is the optimized value of the objective function, and the third value is a return code (negative on failure and positive on success).
Local/subsidiary optimization algorithm
Some of the algorithms, especially MLSL and AUGLAG, use a different optimization algorithm as a subroutine, typically for local optimization. You can change the local search algorithm and its tolerances by setting the opt.local_optimizer field to another optimization structure.
For example, opt.local_optimizer.algorithm = NLOPT_LN_BOBYQA; opt.local_optimizer.ftol_rel = 1e-4 will set the local optimizer to use BOBYQA and a relative function tolerance of 1e-4.
The fields of opt.local_optimizer are used to determine the local search algorithm, its stopping criteria, and other algorithm parameters. (However, the objective function, bounds, and nonlinear-constraint parameters of opt.local_optimizer are ignored.)
Initial step size
Just as in the C API, you can get and set the initial step sizes for derivative-free optimization algorithms. In Matlab, you set the opt.initial_step field to a vector of the (nonzero) initial steps for each dimension.
Stochastic population
Just as in the C API, you can get and set the initial population for stochastic optimization algorithms, by setting opt.population to an (integer) initial population. (An opt.population of zero implies that the heuristic default will be used.)
Vector storage for limited-memory quasi-Newton algorithms
Just as in the C API, you can set the number M of stored vectors for limited-memory quasi-Newton algorithms, via:
opt.vector_storage
(The default is 0, in which case NLopt uses a heuristic nonzero value.)
Verbose output
If you set opt.verbose to 1, the Matlab interface will output information as the optimization progresses, such as the objective function values.
Of course, your objective function and constraints can also output anything you wish, using disp and similar Matlab functions.