Meep Tutorial/Near-to-far-field spectra
From AbInitio
| Revision as of 03:08, 16 April 2015 (edit) Ardavan (Talk | contribs) ← Previous diff |
Revision as of 06:40, 9 January 2016 (edit) Ardavan (Talk | contribs) Next diff → |
||
| Line 9: | Line 9: | ||
| (define-param d1 0.2) | (define-param d1 0.2) | ||
| (define nearfield | (define nearfield | ||
| - | (add-near2far fcen df 1 | + | (add-near2far fcen 0 1 |
| (make near2far-region (center 0 (+ (* 0.5 w) d1)) | (make near2far-region (center 0 (+ (* 0.5 w) d1)) | ||
| (size (- sx (* 2 dpml)) 0)) | (size (- sx (* 2 dpml)) 0)) | ||
| Line 23: | Line 23: | ||
| (run-sources+ (stop-when-fields-decayed 50 Hz (vector3 0.12 -0.37) 1e-8)) | (run-sources+ (stop-when-fields-decayed 50 Hz (vector3 0.12 -0.37) 1e-8)) | ||
| - | |||
| (define-param d2 20) | (define-param d2 20) | ||
| (define-param h 4) | (define-param h 4) | ||
| Line 30: | Line 29: | ||
| (volume (center 0 (+ (* 0.5 w) d2 (* 0.5 h))) (size (- sx (* 2 dpml)) h)) resolution) | (volume (center 0 (+ (* 0.5 w) d2 (* 0.5 h))) (size (- sx (* 2 dpml)) h)) resolution) | ||
| - | The first item to note is that the far-field region is located outside of the computational cell, although in principle it can be located anywhere. The second is that the far-field spectra can be interpolated onto a spatial grid that has any given resolution but in this example we used the same resolution as our simulation. Note that the simulation itself used purely real fields but the output, given its analytical nature, contains complex fields. Finally, given that the far-field spectra is derived from the Fourier-transformed fields which includes an arbitrary constant factor, we should expect an overall scale and phase difference in the results obtained using the near-to-far-field feature with those from a corresponding simulation involving the full computational volume. The key point is that the results will be qualitatively but not quantitatively identical. The data will be written out to an HDF5 file (having a filename prefix with the values of the three main parameters) that will automatically include the far-field spectra for all six field components, including real and imaginary parts. | + | The first item to note is that the far-field region is located <i>outside</i> of the computational cell, although in principle it can be located anywhere. The second is that the far-field spectra can be interpolated onto a spatial grid that has any given resolution but in this example we used the same resolution as the simulation. Note that the simulation itself used purely real fields but the output, given its analytical nature, contains complex fields. Finally, given that the far-field spectra is derived from the Fourier-transformed fields which includes an arbitrary constant factor, we should expect an overall scale and phase difference in the results obtained using the near-to-far-field feature with those from a corresponding simulation involving the full computational volume. The key point is that the results will be qualitatively but not quantitatively identical. The data will be written out to an HDF5 file (having a filename prefix with the values of the three main parameters) that will automatically include the far-field spectra for all six field components, including real and imaginary parts. |
| We run the above modified control file and in post-processing create an image of the real and imaginary parts of <math>H_z</math> over the far-field region which is shown in insets (a) above. For comparison, we compute the steady-state fields with a continuous source (making sure to force the fields to be complex) over the same region in a separate simulation using a larger computational cell that contains within it the far-field region, from which is obtained the images shown in (b). The difference in the relative phases among any two points within each of the two field spectra is zero, which can be confirmed numerically. Also, as would be expected, it can be shown that increasing <code>d1</code> does not change the far-field spectra as long as the results are sufficiently converged (i.e., the resolution is made sufficiently large to mitigate discretization effects). | We run the above modified control file and in post-processing create an image of the real and imaginary parts of <math>H_z</math> over the far-field region which is shown in insets (a) above. For comparison, we compute the steady-state fields with a continuous source (making sure to force the fields to be complex) over the same region in a separate simulation using a larger computational cell that contains within it the far-field region, from which is obtained the images shown in (b). The difference in the relative phases among any two points within each of the two field spectra is zero, which can be confirmed numerically. Also, as would be expected, it can be shown that increasing <code>d1</code> does not change the far-field spectra as long as the results are sufficiently converged (i.e., the resolution is made sufficiently large to mitigate discretization effects). | ||
| - | (In general, it is tricky to interpret the overall scale and phase of the far fields, because it is related to the scaling of the Fourier transforms of the near fields. It is simplest to use the <code>near2far</code> feature in situations where the overall scaling is irrelevant, e.g. when you are computing a ratio of fields in two simulations, or a fraction of the far field in some region, etcetera.) | + | In general, it is tricky to interpret the overall scale and phase of the far fields, because it is related to the scaling of the Fourier transforms of the near fields. It is simplest to use the <code>near2far</code> feature in situations where the overall scaling is irrelevant, e.g. when you are computing a ratio of fields in two simulations, or a fraction of the far field in some region, etcetera. |
Revision as of 06:40, 9 January 2016
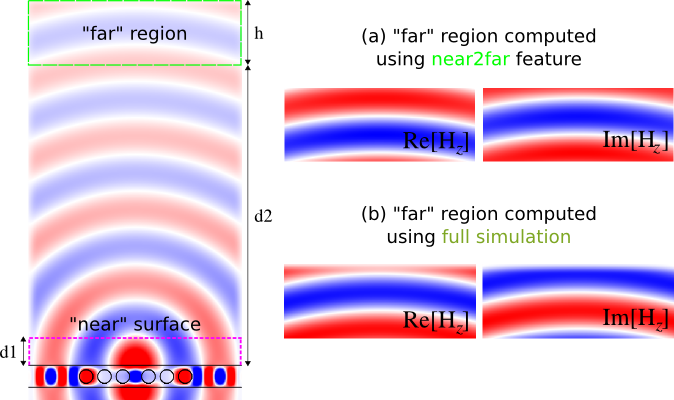
In this example, we demonstrate Meep's near-to-far-field transformation feature, which requires version 1.3+. This feature uses the fields from a "near" bounding surface inside the computational cell to compute the resulting "far" fields outside the computational cell via an analytical transformation. Note that this only works if the "near" surface and the "far" region lie in a single, homogeneous, non-periodic 2d or 3d medium. The analytical transformation is based on the principle of equivalence: given the Fourier-transformed tangential fields on the "near" surface, Meep computes equivalent currents and convolves them with the analytical Green's functions in order to compute the fields at any desired point in the "far" region. The use of the Fourier-transformed fields for this operation is similar to that for the flux and force spectra: we specify a set of desired frequencies, Meep accumulates the Fourier transforms, and then Meep computes the fields at each frequency for the desired far-field points.
There are three steps to using the near-to-far-field feature: first, we need to define the "near" surface(s) as a set of surfaces capturing all outgoing radiation in the desired direction(s); second, we run the simulation, typically with a pulsed source, to allow Meep to accumulate the Fourier transforms on the near surface(s); third, we have Meep compute the far fields at any desired points with the option to save the far fields from a grid of points to an HDF5 file.
For this demonstration, we will compute the far-field spectra of a resonant cavity mode in a holey waveguide; a structure we had explored in a separate tutorial. To do this, we simply modify the last portion of that control file beginning with the following:
(define-param d1 0.2)
(define nearfield
(add-near2far fcen 0 1
(make near2far-region (center 0 (+ (* 0.5 w) d1))
(size (- sx (* 2 dpml)) 0))
(make near2far-region (center (+ (* -0.5 sx) dpml) (+ (* 0.5 w) (* 0.5 d1)))
(size 0 d1)
(weight -1.0))
(make near2far-region (center (- (* 0.5 sx) dpml) (+ (* 0.5 w) (* 0.5 d1)))
(size 0 d1))))
Here, we are creating a "near" bounding surface, consisting of three separate regions surrounding the cavity, that captures all outgoing waves in the top-half of the computational cell. Note that the x-normal surface on the left has a weight of -1 (corresponding to the direction of the outward normal vector relative to the x direction) so that the far-field spectra is correctly computed from the outgoing fields, similar to the flux and force features. The parameter d1 is the distance between the edge of the waveguide and the bounding surface, as shown in the schematic above, and we will demonstrate that changing this parameter does not change the far-field spectra which we compute at a single frequency corresponding to the cavity mode.
We then time step the fields until, at a random point, they have sufficiently decayed away (since the computational cell is surrounded by PMLs) and output the far-field spectra over a rectangular area that lies outside of the computational cell:
(run-sources+ (stop-when-fields-decayed 50 Hz (vector3 0.12 -0.37) 1e-8)) (define-param d2 20) (define-param h 4) (output-farfields nearfield (string-append "spectra-" (number->string d1) "-" (number->string d2) "-" (number->string h)) (volume (center 0 (+ (* 0.5 w) d2 (* 0.5 h))) (size (- sx (* 2 dpml)) h)) resolution)
The first item to note is that the far-field region is located outside of the computational cell, although in principle it can be located anywhere. The second is that the far-field spectra can be interpolated onto a spatial grid that has any given resolution but in this example we used the same resolution as the simulation. Note that the simulation itself used purely real fields but the output, given its analytical nature, contains complex fields. Finally, given that the far-field spectra is derived from the Fourier-transformed fields which includes an arbitrary constant factor, we should expect an overall scale and phase difference in the results obtained using the near-to-far-field feature with those from a corresponding simulation involving the full computational volume. The key point is that the results will be qualitatively but not quantitatively identical. The data will be written out to an HDF5 file (having a filename prefix with the values of the three main parameters) that will automatically include the far-field spectra for all six field components, including real and imaginary parts.
We run the above modified control file and in post-processing create an image of the real and imaginary parts of Hz over the far-field region which is shown in insets (a) above. For comparison, we compute the steady-state fields with a continuous source (making sure to force the fields to be complex) over the same region in a separate simulation using a larger computational cell that contains within it the far-field region, from which is obtained the images shown in (b). The difference in the relative phases among any two points within each of the two field spectra is zero, which can be confirmed numerically. Also, as would be expected, it can be shown that increasing d1 does not change the far-field spectra as long as the results are sufficiently converged (i.e., the resolution is made sufficiently large to mitigate discretization effects).
In general, it is tricky to interpret the overall scale and phase of the far fields, because it is related to the scaling of the Fourier transforms of the near fields. It is simplest to use the near2far feature in situations where the overall scaling is irrelevant, e.g. when you are computing a ratio of fields in two simulations, or a fraction of the far field in some region, etcetera.