Meep Tutorial/Near-to-far-field spectra
From AbInitio
| Revision as of 19:27, 13 April 2015 (edit) Ardavan (Talk | contribs) ← Previous diff |
Revision as of 19:45, 13 April 2015 (edit) Ardavan (Talk | contribs) Next diff → |
||
| Line 1: | Line 1: | ||
| - | In this example, we demonstrate the near-to-far-field transformation feature which requires Meep 1.3+. From the frequency-domain fields obtained using a "near" bounding surface inside the computational cell, we compute the resulting fields outside the computational cell using an analytical transformation. Note that this only works if the "near" surface and the "far" region lie in a single, homogeneous, non-periodic 2d or 3d medium. The analytical transformation is based on the [http://arxiv.org/abs/1301.5366 principle of equivalence]: given the Fourier-transformed tangential fields on the "near" surface, Meep computes equivalent currents and convolves them with the analytical Green's functions in order to compute the fields at any desired point in the "far" region. The use of the Fourier-transformed fields for this operation is similar to the flux and force spectra: we specify a set of desired frequencies, Meep accumulates the Fourier transforms, and then Meep computes the fields at each frequency for the desired far-field points. | + | In this example, we demonstrate the near-to-far-field transformation feature which requires Meep 1.3+. From the fields obtained using a "near" bounding surface inside the computational cell, we compute the resulting "far" fields outside the computational cell using an analytical transformation. Note that this only works if the "near" surface and the "far" region lie in a single, homogeneous, non-periodic 2d or 3d medium. The analytical transformation is based on the [http://arxiv.org/abs/1301.5366 principle of equivalence]: given the Fourier-transformed tangential fields on the "near" surface, Meep computes equivalent currents and convolves them with the analytical Green's functions in order to compute the fields at any desired point in the "far" region. The use of the Fourier-transformed fields for this operation is similar to that for the flux and force spectra: we specify a set of desired frequencies, Meep accumulates the Fourier transforms, and then Meep computes the fields at each frequency for the desired far-field points. |
| There are three steps to using the near-to-far-field feature: first, define the "near" surface(s) as a set of surfaces capturing all outgoing radiation in the desired direction(s); second, run the simulation, typically with a pulsed source, to allow Meep to accumulate the Fourier transforms on the near surface(s); third, tell Meep to compute the far fields at any desired points (optionally saving the far fields from a grid of points to an HDF5 file). | There are three steps to using the near-to-far-field feature: first, define the "near" surface(s) as a set of surfaces capturing all outgoing radiation in the desired direction(s); second, run the simulation, typically with a pulsed source, to allow Meep to accumulate the Fourier transforms on the near surface(s); third, tell Meep to compute the far fields at any desired points (optionally saving the far fields from a grid of points to an HDF5 file). | ||
| Line 5: | Line 5: | ||
| [[Image:N2ff_comp_cell.png|center|Schematic of the computational cell for a holey waveguide with cavity showing the location of the "near" boundary surface and the far-field region.]] | [[Image:N2ff_comp_cell.png|center|Schematic of the computational cell for a holey waveguide with cavity showing the location of the "near" boundary surface and the far-field region.]] | ||
| - | Here, we will compute the far-field spectra of a resonant cavity mode in a holey waveguide; a structure we had explored in a separate [[Meep Tutorial/Band diagram, resonant modes, and transmission in a holey waveguide|tutorial]]. To do this, we simply modify the last portion of the control file beginning with the following: | + | Here, we will compute the far-field spectra of a resonant cavity mode in a holey waveguide; a structure we had explored in a separate [[Meep Tutorial/Band diagram, resonant modes, and transmission in a holey waveguide|tutorial]]. To do this, we simply modify the last portion of that control file beginning with the following: |
| (define-param d1 0.2) | (define-param d1 0.2) | ||
| Line 18: | Line 18: | ||
| (size 0 d1)))) | (size 0 d1)))) | ||
| - | Here, we are creating a "near" bounding surface, consisting of three separate regions surrounding the cavity, that captures <i>all</i> the outgoing waves in the top-half of the computational cell. Note that the <code>y</code>-oriented surface on the left has a <code>weight</code> of -1 so that the flux is accumulated correctly. The parameter <code>d1</code> is the distance between the edge of the waveguide and the bounding surface, as shown in the schematic above, and we will demonstrate that changing this parameter does not change the far-field spectra which we compute at a single frequency corresponding to the cavity mode. | + | Here, we are creating a "near" bounding surface, consisting of three separate regions surrounding the cavity, that captures <i>all</i> outgoing waves in the top-half of the computational cell. Note that the <code>y</code>-oriented surface on the left has a <code>weight</code> of -1 so that the flux is accumulated correctly. The parameter <code>d1</code> is the distance between the edge of the waveguide and the bounding surface, as shown in the schematic above, and we will demonstrate that changing this parameter does not change the far-field spectra which we compute at a single frequency corresponding to the cavity mode. |
| - | We then time step the fields until they have sufficiently decayed away (since the computational cell is surrounded by PMLs) and output the far-field spectra over a rectangular area that lies outside of the computational cell: | + | We then time step the fields until they have sufficiently decayed away (since the computational cell is surrounded by PMLs) and output the far-field spectra over a rectangular area that lies <i>outside</i> of the computational cell: |
| (run-sources+ (stop-when-fields-decayed 50 Hz (vector3 0.12 -0.37) 1e-8)) | (run-sources+ (stop-when-fields-decayed 50 Hz (vector3 0.12 -0.37) 1e-8)) | ||
| Line 28: | Line 28: | ||
| (output-farfields nearfield | (output-farfields nearfield | ||
| (string-append "spectra-" (number->string d1) "-" (number->string d2) "-h" (number->string h)) | (string-append "spectra-" (number->string d1) "-" (number->string d2) "-h" (number->string h)) | ||
| - | (volume (center 0 (+ (* 0.5 w) d2)) (size (- sx (* 2 dpml)) h)) resolution) | + | (volume (center 0 (+ (* 0.5 w) d2 (* 0.5 h))) (size (- sx (* 2 dpml)) h)) resolution) |
| - | The data will be written out to an HDF5 file that will include the far-field spectra for all six field components, including real and imaginary parts. Note that the simulation itself used only purely real fields but the output, given its analytical nature, is for complex fields. Also, the far-field spectra can be interpolated onto a spatial grid that has any given resolution but in this example we used the same resolution as our simulation. Finally, given that the far-field spectra is derived from the Fourier-transformed fields which includes an arbitrary constant factor, we should expect an overall phase difference in the results obtained using the near-to-far-field feature and those from a corresponding simulation with the full computational volume. The key point as we will demonstrate, is that the results will be qualitatively identical. | + | The data will be written out to an HDF5 file that will automatically include the far-field spectra for all six field components, including real and imaginary parts. Note that the simulation itself used purely real fields but the output, given its analytical nature, is for complex fields. Also, the far-field spectra can be interpolated onto a spatial grid that has any given resolution but in this example we used the same resolution as our simulation. Finally, given that the far-field spectra is derived from the Fourier-transformed fields which includes an arbitrary constant factor, we should expect an overall phase difference in the results obtained using the near-to-far-field feature with those from a corresponding simulation having the full computational volume. The key point, as we will demonstrate, is that the results will be qualitatively identical. |
Revision as of 19:45, 13 April 2015
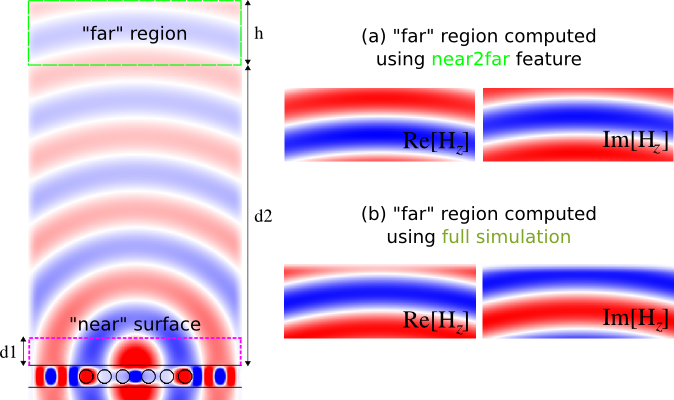
In this example, we demonstrate the near-to-far-field transformation feature which requires Meep 1.3+. From the fields obtained using a "near" bounding surface inside the computational cell, we compute the resulting "far" fields outside the computational cell using an analytical transformation. Note that this only works if the "near" surface and the "far" region lie in a single, homogeneous, non-periodic 2d or 3d medium. The analytical transformation is based on the principle of equivalence: given the Fourier-transformed tangential fields on the "near" surface, Meep computes equivalent currents and convolves them with the analytical Green's functions in order to compute the fields at any desired point in the "far" region. The use of the Fourier-transformed fields for this operation is similar to that for the flux and force spectra: we specify a set of desired frequencies, Meep accumulates the Fourier transforms, and then Meep computes the fields at each frequency for the desired far-field points.
There are three steps to using the near-to-far-field feature: first, define the "near" surface(s) as a set of surfaces capturing all outgoing radiation in the desired direction(s); second, run the simulation, typically with a pulsed source, to allow Meep to accumulate the Fourier transforms on the near surface(s); third, tell Meep to compute the far fields at any desired points (optionally saving the far fields from a grid of points to an HDF5 file).
Here, we will compute the far-field spectra of a resonant cavity mode in a holey waveguide; a structure we had explored in a separate tutorial. To do this, we simply modify the last portion of that control file beginning with the following:
(define-param d1 0.2)
(define nearfield
(add-near2far fcen df 1
(make near2far-region (center 0 (+ (* 0.5 w) d1))
(size (- sx (* 2 dpml)) 0))
(make near2far-region (center (+ (* -0.5 sx) dpml) (+ (* 0.5 w) (* 0.5 d1)))
(size 0 d1)
(weight -1.0))
(make near2far-region (center (- (* 0.5 sx) dpml) (+ (* 0.5 w) (* 0.5 d1)))
(size 0 d1))))
Here, we are creating a "near" bounding surface, consisting of three separate regions surrounding the cavity, that captures all outgoing waves in the top-half of the computational cell. Note that the y-oriented surface on the left has a weight of -1 so that the flux is accumulated correctly. The parameter d1 is the distance between the edge of the waveguide and the bounding surface, as shown in the schematic above, and we will demonstrate that changing this parameter does not change the far-field spectra which we compute at a single frequency corresponding to the cavity mode.
We then time step the fields until they have sufficiently decayed away (since the computational cell is surrounded by PMLs) and output the far-field spectra over a rectangular area that lies outside of the computational cell:
(run-sources+ (stop-when-fields-decayed 50 Hz (vector3 0.12 -0.37) 1e-8))
(define-param d2 18) (define-param h 4) (output-farfields nearfield (string-append "spectra-" (number->string d1) "-" (number->string d2) "-h" (number->string h)) (volume (center 0 (+ (* 0.5 w) d2 (* 0.5 h))) (size (- sx (* 2 dpml)) h)) resolution)
The data will be written out to an HDF5 file that will automatically include the far-field spectra for all six field components, including real and imaginary parts. Note that the simulation itself used purely real fields but the output, given its analytical nature, is for complex fields. Also, the far-field spectra can be interpolated onto a spatial grid that has any given resolution but in this example we used the same resolution as our simulation. Finally, given that the far-field spectra is derived from the Fourier-transformed fields which includes an arbitrary constant factor, we should expect an overall phase difference in the results obtained using the near-to-far-field feature with those from a corresponding simulation having the full computational volume. The key point, as we will demonstrate, is that the results will be qualitatively identical.