Meep Tutorial/Near-to-far-field spectra
From AbInitio
| Revision as of 18:48, 13 April 2015 (edit) Ardavan (Talk | contribs) ← Previous diff |
Revision as of 18:50, 13 April 2015 (edit) Ardavan (Talk | contribs) Next diff → |
||
| Line 1: | Line 1: | ||
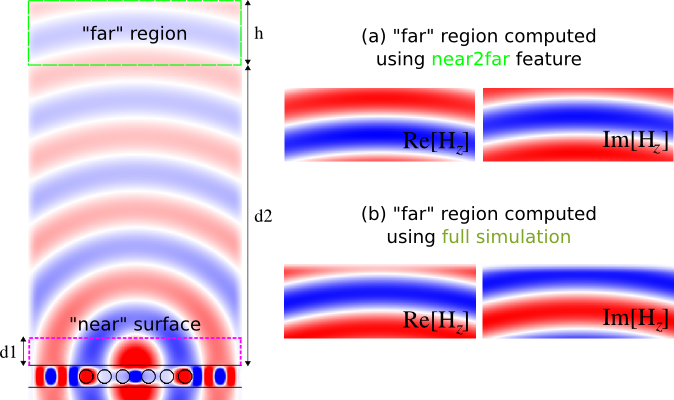
| In this example, we demonstrate the near-to-far-field transformation feature which requires Meep 1.3+. From the frequency-domain fields obtained using a "near" bounding surface inside the computational cell, we compute the resulting fields outside the computational cell using an analytical transformation. Note that this only works if the "near" surface and the "far" region lie in a single, homogeneous, non-periodic 2d or 3d medium. The analytical transformation is based on the principle of equivalence: given the Fourier-transformed tangential fields on the "near" surface, Meep computes equivalent currents and convolves them with the analytical Green's functions in order to compute the fields at any desired point in the "far" region. The use of the Fourier-transformed fields is similar to the flux and force spectra: we specify a set of desired frequencies, Meep accumulates the Fourier transforms, and then Meep computes the fields at each frequency for the desired far-field points. There are three steps to using the near-to-far-field feature: first, define the "near" surface(s) as a set of surfaces capturing all outgoing radiation in the desired direction(s); second, run the simulation, typically with a pulsed source, to allow Meep to accumulate the Fourier transforms on the near surface(s); third, tell Meep to compute the far fields at any desired points (optionally saving the far fields from a grid of points to an HDF5 file). | In this example, we demonstrate the near-to-far-field transformation feature which requires Meep 1.3+. From the frequency-domain fields obtained using a "near" bounding surface inside the computational cell, we compute the resulting fields outside the computational cell using an analytical transformation. Note that this only works if the "near" surface and the "far" region lie in a single, homogeneous, non-periodic 2d or 3d medium. The analytical transformation is based on the principle of equivalence: given the Fourier-transformed tangential fields on the "near" surface, Meep computes equivalent currents and convolves them with the analytical Green's functions in order to compute the fields at any desired point in the "far" region. The use of the Fourier-transformed fields is similar to the flux and force spectra: we specify a set of desired frequencies, Meep accumulates the Fourier transforms, and then Meep computes the fields at each frequency for the desired far-field points. There are three steps to using the near-to-far-field feature: first, define the "near" surface(s) as a set of surfaces capturing all outgoing radiation in the desired direction(s); second, run the simulation, typically with a pulsed source, to allow Meep to accumulate the Fourier transforms on the near surface(s); third, tell Meep to compute the far fields at any desired points (optionally saving the far fields from a grid of points to an HDF5 file). | ||
| - | [[Image:N2ff_comp_cell.png|445px|center|A schematic of the computational cell for a holey waveguide with cavity showing the location of the "near" boundary surface and the far-field region.)] | + | [[Image:N2ff_comp_cell.png|center|Schematic of the computational cell for a holey waveguide with cavity showing the location of the "near" boundary surface and the far-field region.]] |
| Here, we will compute the far-field spectra of a resonant cavity mode in a holey waveguide; a structure we had explored in a separate tutorial. To do this, we simply modify the last portion of the control file beginning with the following: | Here, we will compute the far-field spectra of a resonant cavity mode in a holey waveguide; a structure we had explored in a separate tutorial. To do this, we simply modify the last portion of the control file beginning with the following: | ||
Revision as of 18:50, 13 April 2015
In this example, we demonstrate the near-to-far-field transformation feature which requires Meep 1.3+. From the frequency-domain fields obtained using a "near" bounding surface inside the computational cell, we compute the resulting fields outside the computational cell using an analytical transformation. Note that this only works if the "near" surface and the "far" region lie in a single, homogeneous, non-periodic 2d or 3d medium. The analytical transformation is based on the principle of equivalence: given the Fourier-transformed tangential fields on the "near" surface, Meep computes equivalent currents and convolves them with the analytical Green's functions in order to compute the fields at any desired point in the "far" region. The use of the Fourier-transformed fields is similar to the flux and force spectra: we specify a set of desired frequencies, Meep accumulates the Fourier transforms, and then Meep computes the fields at each frequency for the desired far-field points. There are three steps to using the near-to-far-field feature: first, define the "near" surface(s) as a set of surfaces capturing all outgoing radiation in the desired direction(s); second, run the simulation, typically with a pulsed source, to allow Meep to accumulate the Fourier transforms on the near surface(s); third, tell Meep to compute the far fields at any desired points (optionally saving the far fields from a grid of points to an HDF5 file).
Here, we will compute the far-field spectra of a resonant cavity mode in a holey waveguide; a structure we had explored in a separate tutorial. To do this, we simply modify the last portion of the control file beginning with the following:
(define-param d1 0.2)
(define nearfield
(add-near2far fcen df 1
(make near2far-region (center 0 (+ (* 0.5 w) d1))
(size (- sx (* 2 dpml)) 0))
(make near2far-region (center (+ (* -0.5 sx) dpml) (+ (* 0.5 w) (* 0.5 d1)))
(size 0 d1)
(weight -1.0))
(make near2far-region (center (- (* 0.5 sx) dpml) (+ (* 0.5 w) (* 0.5 d1)))
(size 0 d1))))
Here we are creating a "near" bounding surface, consisting of three separate regions surrounding the cavity, that captures all the outgoing waves in the top-half of the computational cell. Note that the y-oriented surface on the left has a weight of -1 so that the flux is accumulated correctly. The parameter d1 is the distance between the edge of the waveguide and the bounding surface and we will demonstrate that changing this parameter does not change the far-field spectra. We are also computing the far-field spectra at just the frequency corresponding to the cavity mode.
(run-sources+ (stop-when-fields-decayed 50 Hz (vector3 0.12 -0.37) 1e-8))
(define-param d2 18) (define-param h 4) (output-farfields nearfield (string-append "data-" (number->string d1) "-" (number->string d2) "-res" (number->string resolution)) (volume (center 0 (+ (* 0.5 w) d2)) (size (- sx (* 2 dpml)) h)) resolution)