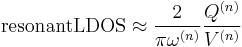Meep Tutorial/Local density of states

From AbInitio

In this example, we will demonstrate the LDOS feature of Meep by investigating the Purcell enhancement phenomena in a metallic microcavity. The LDOS, in general, has many important uses for understanding classical dipole sources, but also in many physical phenomena that can be understood semiclassically in terms of dipole currents -- for example, the spontaneous emission rate of atoms (key to fluorescence and lasing phenomena) is proportional to the LDOS. In simple terms, the LDOS is really just a measure of how much the harmonic modes of a system overlap with the source point (proportional, as well, to the radiation resistance of a dipole antenna) and is a key quantity in electromagnetism due to the fact that the same current radiates a different amount of power depending on the surrounding geometry. Analytically, the per-polarization LDOS is exactly proportional to the power radiated by an 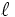-oriented point-dipole current at a given position in space. For a more mathematical treatment of the theory behind the LDOS, we refer you to the relevant discussion in chapter 4 of our upcoming book, but for now we simply give the result:

where the 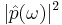normalization is necessary for obtaining the power exerted by a unit-amplitude dipole (assuming linear materials). In FDTD, computing the LDOS therefore is straightforward: excite a point dipole source and accumulate the Fourier transforms of the field at a given point in space to obtain the entire LDOS spectrum in a single calculation.

A lossless localized mode yields a δ-function spike in the LDOS, whereas a lossy (i.e. arising from either small absorption or radiation) localized mode -- a resonant cavity mode -- leads to a Lorentzian peak. The large enhancement in the LDOS at the resonant peak is known as a Purcell effect, named after Purcell's proposal for enhancing spontaneous emission of an atom in a cavity (analogous to a microwave antenna resonating in a metal box). In this case, the resonant mode's contribution to the LDOS at ω⁽ⁿ⁾ can be shown to be:

where Q⁽ⁿ⁾ = ω⁽ⁿ⁾ / 2γ⁽ⁿ⁾ is the dimensionless quality factor and V⁽ⁿ⁾ is the modal volume. This represents another way to compute the LDOS and in this tutorial, we will verify this expression by comparing it to the earlier expression which is a built-in feature.

Here, we consider the simple example of a two-dimensional perfect-metal axa cavity of finite thickness 0.1a, with a small notch of width w on one side that allows the modes to escape. The nice thing about this example is that in the absence of the notch, the lowest-frequency TM-polarized mode is known analytically to be 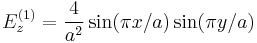, with a frequency 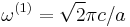and modal volume V⁽¹⁾ = a² / 4. The notch slightly perturbs this solution, but more importantly the notch allows it to radiate out into the surrounding air, yielding a finite Q. For , this radiative escape occurs via an evanescent (sub-cutoff) mode of the channel waveguide formed by the notch, and it follows from inspection of the evanescent decay rate 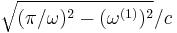that the lifetime scales asymptotically as 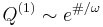for some coefficient #. We will validate both this prediction and the LDOS calculations above by computing the LDOS at the center of the cavity (the point of peak 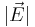) in two ways. First, we compute the LDOS directly from the power radiated by a dipole, Fourier-transforming the result of a pulse which is done automatically for you as a built-in feature. Second, we compute the cavity mode and its lifetime Q using harminv and then compute the LDOS by the Purcell formula shown above. The latter technique is much more efficient for high Q (small w), since one must run the simulation for a very long time to directly accumulate the Fourier transform of a slowly decaying mode. The two calculations agree (to within a discretization error), verifying the LDOS analysis above, and Q / V is asymptotically linear on a semilog scale versus 1 / w as predicted.