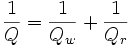Meep Tutorial/Band diagram, resonant modes, and transmission in a holey waveguide
From AbInitio
| Revision as of 04:03, 7 November 2005 (edit) Stevenj (Talk | contribs) (→Band diagram) ← Previous diff |
Revision as of 19:52, 10 November 2005 (edit) Mihai (Talk | contribs) (→Band diagram - thumbnail for image) Next diff → |
||
| Line 221: | Line 221: | ||
| ==Band diagram== | ==Band diagram== | ||
| - | [[Image:Holey-wvg-bands-eps-000000.00.png|right|Unit cell of ε for periodic waveguide]] | + | [[Image:Holey-wvg-bands-eps-000000.00.png|thumb|84px|right|Unit cell of ε for periodic waveguide]] |
| Finally, we consider a smaller, more abstract calculation that we really should have done first, if it hadn't already been done in the 1995 paper. In particular, we compute the '''band diagram''' of the '''infinite periodic waveguide''' by itself (with no defects). (This is very similar to the types of calculations that [[MPB]] performs, but with a different method that has its own strengths and weaknesses.) By analyzing what solutions can propagate in the periodic structure, one gains fundamental insight into the aperiodic structures above. | Finally, we consider a smaller, more abstract calculation that we really should have done first, if it hadn't already been done in the 1995 paper. In particular, we compute the '''band diagram''' of the '''infinite periodic waveguide''' by itself (with no defects). (This is very similar to the types of calculations that [[MPB]] performs, but with a different method that has its own strengths and weaknesses.) By analyzing what solutions can propagate in the periodic structure, one gains fundamental insight into the aperiodic structures above. | ||
Revision as of 19:52, 10 November 2005
| Meep |
| Download |
| Release notes |
| FAQ |
| Meep manual |
| Introduction |
| Installation |
| Tutorial |
| Reference |
| C++ Tutorial |
| C++ Reference |
| Acknowledgements |
| License and Copyright |
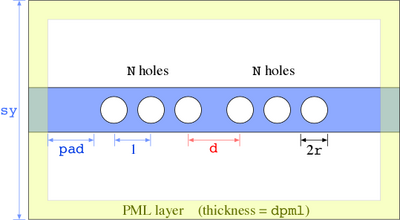
In this example, we will consider the two-dimensional structure shown above, which is based on a system considered in:
- S. Fan, J. N. Winn, A. Devenyi, J. C. Chen, R. D. Meade, and J. D. Joannopoulos, "Guided and defect modes in periodic dielectric waveguides," J. Opt. Soc. Am. B. 12 (7), 1267-1272 (1995).
In particular, there are three basic ideas behind this structure, which we briefly summarize here.
First, by taking a dielectric wavgeuide and perforating it with a periodic sequence of holes, we form a kind of photonic crystal: there are still index-guided modes propagating losslessly down the periodic waveguide, but there is also a (partial) photonic band gap: a range of frequencies in which no guided modes exist.
Second, by making a defect in the periodic sequence, in this case by separating one pair of holes by a greater amount, we can trap a resonant cavity mode: it is localized along the waveguide direction by the band gap, and (partially) in the transverse direction by index-guiding. Because there is no complete gap, however, the mode has some intrinsic radiative losses: even with infinitely many holes/periods, it leaks away slowly into the surrounding air.
Third, by making a sequence of: ordinary (no holes) waveguide, periodic structure, defect, periodic structure, waveguide, we can make a filter. In particular, because there is now a finite number of holes, the resonant mode can now leak into the waveguide as well as to the surrounding air. Then, input light from the waveguide at the resonance frequency undergoes resonant coupling, and is transmitted to the other side with a Lorentzian transmission spectrum. In the limit where the resonant mode couples much more strongly with the waveguide than the air (i.e. if there are not too many holes and the radiative leakage is slow), then in a symmetric structure we should get 100% transmission on resonance, forming a narrow-band filter.
In the following, we will analyze the structure in exactly the opposite order of what we really should do. Really, we should analyze the periodic system first to understand the band gap, then analyze the resonant mode, and then finally analyze the transmission spectrum. Since all of those calculations have already been done in the above paper, however, we can jump straight to the transmission spectrum (which is conceptually the easiest computation to understand) and work backwards.
See also the holey-wvg-cavity.ctl and holey-wvg.ctl files included with Meep, which contain the commands below.
Contents |
Transmission spectrum
To calculate the transmission spectrum, much as in the bend example in the Meep tutorial, we'll measure the flux spectrum at one end of the waveguide from a source at the other end, normalized by the flux from a case with no holes in the waveguide. First, we'll define some parametes defining our structure, as in the figure above; note that we'll choose units so that our periodicity is 1 (a typical choice for photonic crystals).
; Some parameters to describe the geometry: (define-param eps 13) ; dielectric constant of waveguide (define-param w 1.2) ; width of waveguide (define-param r 0.36) ; radius of holes (define-param d 1.4) ; defect spacing (ordinary spacing = 1) (define-param N 3) ; number of holes on either side of defect ; The cell dimensions (define-param sy 6) ; size of cell in y direction (perpendicular to wvg.) (define-param pad 2) ; padding between last hole and PML edge (define-param dpml 1) ; PML thickness
Given these parameters, the size of the cell in the x direction, which we'll denote sx, is given by sx = 2*(pad+dpml+N) + d - 1, which in Scheme is expressed as:
(define sx (+ (* 2 (+ pad dpml N)) d -1)) ; size of cell in x direction
Now, the computational cell is:
(set! geometry-lattice (make lattice (size sx sy no-size)))
Our geometry will consist of a single block for the waveguide, and 2N cylindrical holes. To make the holes, we could use some kind of loop (see also how to write a loop in Scheme), but in this case it is even easier to to use the predefined function geometric-object-duplicates, which replicates a given object by shifting by a given vector a given number of times (see the Meep reference):
(set! geometry
(append ; combine lists of objects:
(list (make block (center 0 0) (size infinity w infinity)
(material (make dielectric (epsilon eps)))))
(geometric-object-duplicates (vector3 1 0) 0 (- N 1)
(make cylinder (center (/ d 2) 0) (radius r) (height infinity)
(material air)))
(geometric-object-duplicates (vector3 -1 0) 0 (- N 1)
(make cylinder (center (/ d -2) 0) (radius r) (height infinity)
(material air)))))
Note that we call geometric-object-duplicates twice, for the holes before and after the defect, and that we combine the resulting lists with the standard Scheme append function. As usual, later objects in geometry take precedence over earlier objects, so the cylinder objects will punch holes through the block.
The absorbing boundaries are:
(set! pml-layers (list (make pml (thickness dpml)))) (set-param! resolution 20)
Now, we'll define a couple of parameters to determine the frequency range to look at. We already know from the 1995 paper (or our calculation below) that this structure has a TE band gap for frequencies from about 0.2 to 0.3, so we'll want to cover this range.
(define-param fcen 0.25) ; pulse center frequency (define-param df 0.2) ; pulse width (in frequency) (define-param nfreq 500) ; number of frequencies at which to compute flux
The source will now be the usual Gaussian pulse centered at fcen, located at one edge of the cell just outside the PML, at x = dpml - 0.5*sx. Ideally, we would excite exactly the fundamental mode of the waveguide, but it is good enough to just excite it with a line source. Moreover, since we are interested in the TE polarization (electric field in the plane), we will excite it with a Jy current source (transverse to the propagation direction), which is specified as Ey:
(set! sources (list
(make source
(src (make gaussian-src (frequency fcen) (fwidth df)))
(component Ey)
(center (+ dpml (* -0.5 sx)) 0)
(size 0 w))))
The structure has mirror symmetry planes through the x and y axes. The source breaks the mirror symmetry through the y axis, but we still have odd mirror symmetry through the x axis:
(set! symmetries (list (make mirror-sym (direction Y) (phase -1))))
Note that we specify the plane by its normal, the y direction. See also: Exploiting symmetry in Meep.
Finally, we need to tell Meep to compute the flux spectrum at the other end of the computational cell, after the holes but before the PML:
(define trans ; transmitted flux
(add-flux fcen df nfreq
(make flux-region
(center (- (* 0.5 sx) dpml 0.5) 0) (size 0 (* w 2)))))
Now, we can run the simulation, using run-sources+ to run until the sources have finished, plus some additional time to allow the fields to propagate through the structure. As in the Meep tutorial, we'll use stop-when-fields-decayed to increment the time in steps of 50 time units (about 13 periods) until | Ey | 2 has decayed by at least 1/1000 at the transmission-flux plane.
(run-sources+ (stop-when-fields-decayed
50 Ey
(vector3 (- (* 0.5 sx) dpml 0.5) 0)
1e-3)
(at-beginning output-epsilon)
(during-sources
(in-volume (volume (center 0 0) (size sx 0))
(to-appended "hz-slice" (at-every 0.4 output-hfield-z)))))
(display-fluxes) ; print out the flux spectrum
Note that we've outputted ε at the beginning—this is always a good idea, to make sure the structure is what you think it is! We have also outputted the Hz field in a y = 0 slice, every 0.4 time units (about ten times per period) while the source is on, to a single file with time as the second dimension, just as in the Meep tutorial. Now, after we run the simulation:
unix% meep holey-wvg-cavity.ctl | tee holey-wvg-cavity.out
(which takes some time because we need to wait for the cavity mode to decay away) we can plot the dielectric function and Hz field pattern via h5topng:
unix% h5topng holey-wvg-cavity-eps-000000.00.h5 unix% h5topng -Zc dkbluered holey-wvg-cavity-hz-slice.h5
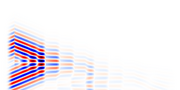
The Hz slice (in which time = vertical) is interesting, because we can see the pulse propagating to the right, bouncing off of the holes, and also exciting a resonant mode in the cavity that sits in the center for a long time as it starts slowly leaking to the right.
Of course, the main point of this section is to get the quantitative transmission spectrum. To do this, we need to normalize our flux by running the simulation with no holes:
unix% meep N=0 holey-wvg-cavity.ctl | tee holey-wvg-cavity.out0
which completes a lot more quickly because there is no resonant mode. We then grep for the flux as in the tutorial, giving us comma-delimited text which is the frequency and fluxes:
unix% grep flux1: holey-wvg-cavity.out > flux.dat unix% grep flux1: holey-wvg-cavity.out0 > flux0.dat
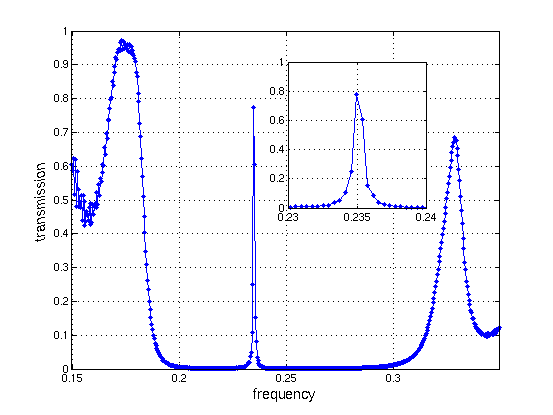
which we then import into our plotting program, divide the two fluxes, and get:
The band gap is clearly visible as the range of very low transmission, and in the middle of the band gap is a sharp peak corresponding to the resonant mode trapped in the defect. The inset enlarges this peak, and shows that we didn't use quite enough frequency points to capture the whole shape (although we could fit to a Lorentzian if we wanted). At the edges of the band gaps, the transmission goes up in broad Fabry-Perot resonance peaks (which we will examine in more detail below). There is also some high-frequency oscillation visible at the left of the plot, which is a numerical artifact due to our pulse not having enough amplitude in that range.
The narrower the resonance peak (higher Q), the harder this sort of direct transmission simulation is to perform—because of the Fourier uncertainty principle, we need to run for a time inversely related to the frequency resolution we would like to obtain. Fortunatly, there is a much better way to study high-Q resonances, as described in the next section (see also the ring resonators in the Meep tutorial).
Resonant modes
To study high-Q (long lifetime) resonant modes, it is much more efficient to excite them directly, placing a source inside the cavity, and analyze the resulting fields to obtain the frequencies and lifetimes of the modes. Here, we do precisely that for the above structure. See also the ring-resonator example and the resonant-modes introduction.
The structure is exactly the same as above, and only the sources and analysis are different. Because of that, we use the same holey-wvg-cavity.ctl input file for both calculations, and select between the two with an if statement controlled by a compute-mode? variable:
; false = transmission spectrum, true = resonant modes:
(define-param compute-mode? false)
(if compute-mode?
(begin
...new sources and run command...
)
(begin
...sources and run from above, to get spectrum...
))
The (begin ...) is a standard Scheme construct to group several statements into one, much like {...} brackets in C. Our new source is still a Gaussian, but is now a point source at the origin:
(set! sources (list
(make source
(src (make gaussian-src (frequency fcen) (fwidth df)))
(component Hz) (center 0 0))))
Moreover, we are now using a magnetic current oriented in the z direction (Hz). This source matches the symmetry of the TE resonant mode that we are looking for. If we didn't know in advance what symmetry we were looking for, we would put the source off-center in a non-symmetric location, which would excite all modes regardless of symmetry. However, in many cases the symmetry is known, and placing a symmetric source allows us to limit the number of modes we excite and also to exploit the fact that we now have two mirror symmetry planes in this problem, saving us a factor of four in computation:
(set! symmetries
(list (make mirror-sym (direction Y) (phase -1))
(make mirror-sym (direction X) (phase -1))))
Here, you may notice a strange thing: we have specified (phase -1) for both mirror planes corresponding to odd symmetry. However, it may seem at first glance that an Hz dipole at the origin has even symmetry! The subtlety here is that the magnetic field is a pseudovector, and is multiplied by − 1 under mirror flips, so it is odd when it looks even and vice versa. We aren't just being pedantic here—if you don't realize the difference between vectors (such as electric fields and currents) and pseudovectors (such as magnetic fields and currents), then you will have endless confusion because the electric and magnetic fields will seem to have different symmetry. See also Exploiting symmetry in Meep.
Finally, we can run:
(run-sources+ 400
(at-beginning output-epsilon)
(after-sources (harminv Hz (vector3 0) fcen df)))
(run-until (/ 1 fcen) (at-every (/ 1 fcen 20) output-hfield-z))
Just as in the ring-resonator example, we use the harminv command (which calls Harminv) to analyze the response at a point (here the Hz field at the origin) for some time after the source has turned off. At the end, we also output the Hz field for one period, to help us visualize the field below.
We can now run the simulation, setting compute-mode?=true to do the resonant-mode calculation:
unix% meep compute-mode?=true holey-wvg-cavity.ctl
Inspecting the output, we see that it finds a single resonant mode in the gap:
harminv0:, frequency, imag. freq., Q, |amp|, amplitude, error harminv0:, 0.235109393214226, -3.14979827803982e-4, 373.213413146792, 9.44684723593584, 6.69397286173395-6.66585703608155i, 3.35873386748359e-9
Because it was a single high-Q mode, this mode should be all that we have left at the end of the simulation:
unix% h5topng -RZc dkbluered -C holey-wvg-cavity-eps-000000.00.h5 holey-wvg-cavity-hz-*.h5 unix% convert holey-wvg-cavity-hz-*.png holey-wvg-cavity-hz.gif
The mode has a frequency of 0.235, just as we saw in the transmission spectrum, and a Q of 373 (which we could have also found by fitting the transmission spectrum). This lifetime Q includes two independent decay channels: light can decay from the cavity into the waveguide with lifetime Qw, or it can radiate from the cavity into the surrounding air with lifetime Qr, where
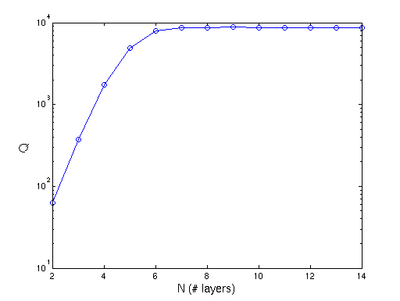
There are a variety of ways to separate out the two decay channels. For example, we can look at the power radiated in different directions. Here, we'll just increase the number N of holes and see what happens—as we increase N, Qw should increase exponentially while Qr remains roughly fixed, so that Q eventually saturates at Qr.
unix% meep N=4 compute-mode?=true holey-wvg-cavity.ctl |grep harminv unix% meep N=5 compute-mode?=true holey-wvg-cavity.ctl |grep harminv ...
The results, shown above, are exactly what we expected: at first, an exponential increase of Q with N, and then a saturation at 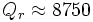 . However, when we look at the
. However, when we look at the harminv output for larger N, something strange happens—it starts to find more modes! For example, at N=16, the output is:
harminv0:, frequency, imag. freq., Q, |amp|, amplitude, error harminv0:, 0.235201161007777, -1.34327185513047e-5, 8754.78631184943, 9.83220617825986, 6.83285024080876-7.06996717944934i, 3.03237056700397e-9 harminv0:, 0.328227374843021, -4.6405752015136e-4, 353.649451404175, 0.134284355228178, -0.131856646632894-0.0254187489419837i, 4.11557526694386e-7
What is this extra mode at ω = 0.32823? This is right around the edge of the band gap (actually, just above the edge). There are two possibilities. First, it could be a band edge state: the propagating states in the periodic waveguide go to zero group velocity as they approach the edge of the gap, corresponding to long-lived resonances in a long but finite crystal. Second, it could be a higher-order resonant mode that for a slightly larger defect will be pulled further into the gap, but is currently very delocalized. In this case, it turns out to be the latter. To see the mode, we will simply run the simulation again with a narrow-band source, and we will also increase the y cell size sy because it turns out that the mode is fairly spread out in that direction:
unix% meep sy=12 fcen=0.328227374843021 df=0.01 N=16 compute-mode?=true holey-wvg-cavity.ctl
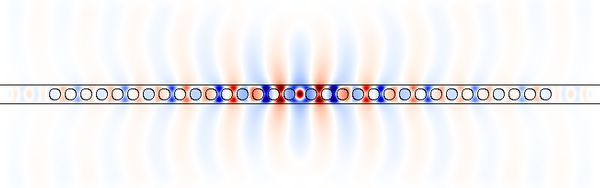
From the image, the field is clearly localized around the defect in the center (as opposed to being spread out evenly in the crystal like a band-edge state would be), and in the defect the pattern is higher order than the previous mode (it has an extra pair of nodes in the y direction).
Band diagram
Finally, we consider a smaller, more abstract calculation that we really should have done first, if it hadn't already been done in the 1995 paper. In particular, we compute the band diagram of the infinite periodic waveguide by itself (with no defects). (This is very similar to the types of calculations that MPB performs, but with a different method that has its own strengths and weaknesses.) By analyzing what solutions can propagate in the periodic structure, one gains fundamental insight into the aperiodic structures above.
Let us briefly review the problem (see the above paper for more information, or the book Photonic Crystals: Molding the Flow of Light by Joannopoulos et al.). In a periodic system of this sort, the eigen-solutions can be expressed in the form of Bloch modes: a periodic Bloch envelope multiplied by a planewave ![\exp[i(\mathbf{k}\cdot\mathbf{x}-\omega t)]](/wiki/images/math/3/d/2/3d2ba22314ea0686d4c5550cff2b9da1.png) , where k is the Bloch wavevector. We wish to find the bands
, where k is the Bloch wavevector. We wish to find the bands 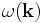 . In this case, there is only one direction of periodicity, so we only have one wavevector component kx. Moreover, the solutions are periodic functions of this wavevector: for a unit-period structure, kx and kx + 2π are redundant. Also, kx and − kx are redundant by time-reversal symmetry, so we only need to look for solutions in the irreducible Brillouin zone from kx = 0 to kx = π.
. In this case, there is only one direction of periodicity, so we only have one wavevector component kx. Moreover, the solutions are periodic functions of this wavevector: for a unit-period structure, kx and kx + 2π are redundant. Also, kx and − kx are redundant by time-reversal symmetry, so we only need to look for solutions in the irreducible Brillouin zone from kx = 0 to kx = π.
Solving for these eigenmodes is very similar to solving for the resonant modes of a cavity (we put in a pulse and analyze the response via harminv), except that our computational cell and boundary conditions are different. In particular, our computational cell is simply the unit cell of the periodicity, shown at right. The ε function then obeys periodic boundary conditions, but the fields obey Bloch-periodic boundary conditions: the fields at the right side are 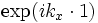 times the fields at the left side. For each kx, we will do a separate computation to get the frequencies at that kx.
times the fields at the left side. For each kx, we will do a separate computation to get the frequencies at that kx.
Thus, we will define our computational cell via (see also the holey-wvg-bands.ctl file included with Meep):
; Some parameters to describe the geometry:
(define-param eps 13) ; dielectric constant of waveguide
(define-param w 1.2) ; width of waveguide
(define-param r 0.36) ; radius of holes
; The cell dimensions
(define-param sy 12) ; size of cell in y direction (perpendicular to wvg.)
(define-param dpml 1) ; PML thickness (y direction only!)
(set! geometry-lattice (make lattice (size 1 sy no-size)))
(set! geometry
(list (make block (center 0 0) (size infinity w infinity)
(material (make dielectric (epsilon eps))))
(make cylinder (center 0 0) (radius r) (height infinity) (material air))))
(set-param! resolution 20)
Note that our cell is now size 1 in the x direction, and there is no need for geometric-object-duplicate—we just have a single air hole in the unit cell. The PML absorbing boundaries have something new:
(set! pml-layers (list (make pml (direction Y) (thickness dpml))))
Since our structure is periodic, we don't want any absorbing layers in the x direction: adding (direction Y) just specifies PML layers on the y boundaries.
As before, our source will be a Gaussian pulse from a magnetic (Hz) point source:
(define-param fcen 0.25) ; pulse center frequency
(define-param df 1.5) ; pulse freq. width: large df = short impulse
(set! sources (list
(make source
(src (make gaussian-src (frequency fcen) (fwidth df)))
(component Hz) (center 0.1234 0))))
Notice that we put our source at (0.1234,0). The x coordinate is "random", to help ensure that the source will couple to an arbitrary mode, but the y coordinate is 0 — this means that we will only be looking at TE-polarized odd-symmetry modes (recalling the pseudovector subtlety discussed above). As usually, we will exploit this via:
(set! symmetries (list (make mirror-sym (direction Y) (phase -1))))
(Note that, regardless of the source, we don't have an X symmetry plane because this symmetry is broken by our boundary condition for 0 < kx < π.) Now, there are two ways to proceed. First, we could set the value of 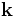 via the
via the k-point variable, and then use run-sources+ with harminv just as we did to calculate a resonant mode:
(set-param! k-point (vector3 0.4 0)) (run-sources+ 300 (after-sources (harminv Hz (vector3 0.1234) fcen df)
which would give us the frequencies at a single 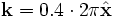 . Note that, in Meep,
. Note that, in Meep, 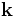 is specified as a vector in Cartesian coordinates, with units of 2π/distance. (This is different from MPB, which uses the basis of the reciprocal lattice vectors!) However, this only gives us one
is specified as a vector in Cartesian coordinates, with units of 2π/distance. (This is different from MPB, which uses the basis of the reciprocal lattice vectors!) However, this only gives us one 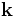 . Instead, there is a built-in function
. Instead, there is a built-in function run-k-points, which takes as input a time to run after the sources finish (like the 300 above) and a list of 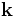 points:
points:
(define-param k-interp 19) (run-k-points 300 (interpolate k-interp (list (vector3 0) (vector3 0.5))))
Here, we have used libctl's built-in interpolate function to interpolate a set of 19 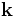 points between
points between 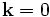 and
and 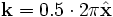 , to cover the irreducible Brillouin zone.
, to cover the irreducible Brillouin zone. run-k-points automatically runs harminv, using the frequency range and location taken from the Gaussian source in the sources list. (It also calls output-epsilon.) The output is not only the usual harminv: lines, but it also outputs a series of lines like:
freqs:, 14, 0.325, 0.0, 0.0, 0.171671252741341, 0.319717964514696, 0.323470450791478 freqs-im:, 14, 0.325, 0.0, 0.0, -8.74808991364674e-8, 1.82230861728163e-4, 0.00144227925408331
where the first numeric column is an index (1, 2, 3, ...), the next three columns are the components of 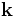 , and the remaining columns are the real part of ω (for the
, and the remaining columns are the real part of ω (for the freqs: lines) or the imaginary part of ω (for the freqs-im: lines). Now we can just do:
unix% meep holey-wvg-bands.ctl | tee holey-wvg-bands.out unix% grep freqs: holey-wvg-bands.out > fre.dat unix% grep freqs-im: holey-wvg-bands.out > fim.dat
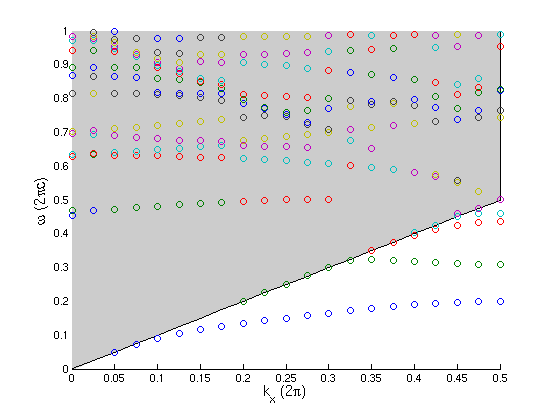
Plotting the real parts of ω, we find:
Here, the gray shaded region is the light cone, ω > ckx, which is the region corresponding to modes that are extended in the air surrounding the waveguide. Below the light cone, we see several discrete guided bands, which must have field patterns localized to the vicinity of the waveguide. The imaginary part of ω for bands below the light cone is very small, due to either numerical error or the finite computational cell size (some tiny portion of the guided mode overlaps the PML). Note the band gap between the first and second guided mode, from about 0.2 to 0.3.
Inside the light cone, we also see several discrete bands. These are leaky modes, or resonances, which have some intrinsic lifetime/loss because they couple with radiating states inside the light cone, which is reflected in the imaginary parts of their ω. (Twice the imaginary part of ω is the energy loss rate per unit time; for a waveguide, it is more conventional to report loss per unit distance; to get this you would divide the loss per unit time by the group velocity | dω / dkx | = |slope|.) Harminv only identifies leaky modes that have a substantial lifetime (the default threshold is a lifetime, or Q, of 50 periods).
Computing band diagrams, especially for leaky modes, with a time-domain program like Meep involves several subtleties. For example, the accuracy of harminv will go down if we specify too large a df (too narrow a source), because the increased number of modes makes the signal-processing more ill-conditioned. Sometimes, harminv will report a spurious mode, which will appear as an isolated dot on the plot. Second, we sometimes have to be careful with modes and especially the imaginary parts to make sure they aren't an artifact of the cell being too small, or the signal-processing error being too large (either because the run is too short or because the bandwidth being searched is too large). Third, currently Meep doesn't attempt to "connect the dots" for the bands—the frequencies are printed in increasing order, but since modes disappear when their losses become too large this means that a single band may be split across several columns (on the plot, this is visible as single bands composed of differently colored dots).
For example, there seem to be some bands that run right along the edge of the light cone. These are not leaky modes, but are artifacts of the fact that PML boundaries do not absorb well for light that is travelling parallel to the boundary, corresponding to extended modes at the boundary of the light cone. Below, we will see that these modes are not localized to the waveguide.
It is usually a good idea to examine the field patterns for any modes that you are particularly interested in. That is, re-run the simulation with a narrow-bandwidth source, at the particular ω and 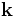 you want, and output the field patterns just as we did for the resonant-cavity modes. We have done that for several modes below:
you want, and output the field patterns just as we did for the resonant-cavity modes. We have done that for several modes below:
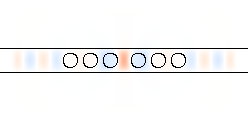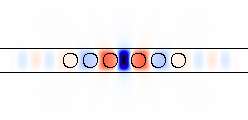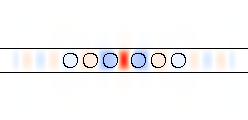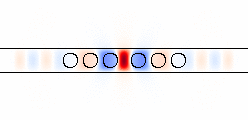
| kx = 0.4, ω = 0.1896 guided mode | kx = 0.4, ω = 0.3175 guided mode | kx = 0.1, ω = 0.4811 − 0.0017i leaky mode | kx = 0.3, ω = 0.8838 − 0.0018i leaky mode | kx = 0.25, ω = 0.2506 light-cone (extended) mode |
- From the left, the first two pictures show the first two guided bands underneath the light cone at kx = 0.4. Note that the second guided band is propagating to the left, which is due to its negative slope (note that there is a corresponding right-propagating mode at kx = − 0.4. Note that they are strongly (exponentially) localized to the waveguide, as they should be.
- The next mode is the first leaky mode at kx = 0.1. As kx goes to zero, in fact, this mode actually becomes lossless, a peculiarity of symmetry related to an effect demonstrated by Ochiai and Sakoda [Phys. Rev. B. 63, 125107 (2001)]. However, at this non-zero kx, the radiation loss is clearly visible.
- The next mode is one of the many higher-order leaky modes visible in the band diagram; we arbitrarily chose the backwards-propagating mode at kx = 0.3, ω = 0.8838 − 0.0018i to plot. As can be seen from the field pattern, this mode has a very short wavelength in the material. This is short enough that it is worth checking how big the error introduced by the finite resolution is. By doubling the resolution to 40 pixels/unit, we found that this mode has shifted to ω = 0.8996 − 0.0021i, or about a 2% error at the lower resolution.
- Finally, we show one of the modes right along the edge of the light cone, at kx = 0.25, ω = 0.2506. This mode is clearly not localized to the waveguide, and is just propagating through the air parallel to the waveguide—i.e. it is really part of the continuum of extended modes and its discreteness is an artifact of the finite cell and imperfect boundary conditions. For light propagating completely parallel to the boundary, PML is not very effective, so the imaginary part of ω is only -0.0008 for this field.