Meep Tutorial
From AbInitio
| Revision as of 22:41, 26 October 2005 (edit) Stevenj (Talk | contribs) (→Fields in a waveguide) ← Previous diff |
Revision as of 02:24, 27 October 2005 (edit) Stevenj (Talk | contribs) (→Fields in a waveguide) Next diff → |
||
| Line 32: | Line 32: | ||
| Before we define the structure, however, we have to define the computational cell. We're going to put a source at one end and watch it propagate down the waveguide in the ''x'' direction, so let's use a cell of length 15 in the ''x'' direction to give it some distance to propagate. In the ''y'' direction, we just need enough room so that the boundaries (below) don't affect the waveguide mode; let's give it a size of 8. We now specify these sizes in our ctl file via the <code>geometry-lattice</code> variable: | Before we define the structure, however, we have to define the computational cell. We're going to put a source at one end and watch it propagate down the waveguide in the ''x'' direction, so let's use a cell of length 15 in the ''x'' direction to give it some distance to propagate. In the ''y'' direction, we just need enough room so that the boundaries (below) don't affect the waveguide mode; let's give it a size of 8. We now specify these sizes in our ctl file via the <code>geometry-lattice</code> variable: | ||
| - | (set! geometry-lattice (make lattice (size 15 8 no-size))) | + | (set! geometry-lattice (make lattice (size 16 8 no-size))) |
| (The name <code>geometry-lattice</code> comes from [[MPB]], where it can be used to define a more general periodic lattice. Although Meep supports periodic structures, it is less general than MPB in that affine grids are not supported.) <code>set!</code> is a Scheme command to set the value of an input variable. The last <code>no-size</code> parameter says that the computational cell has no size in the ''z'' direction, i.e. it is two-dimensional. | (The name <code>geometry-lattice</code> comes from [[MPB]], where it can be used to define a more general periodic lattice. Although Meep supports periodic structures, it is less general than MPB in that affine grids are not supported.) <code>set!</code> is a Scheme command to set the value of an input variable. The last <code>no-size</code> parameter says that the computational cell has no size in the ''z'' direction, i.e. it is two-dimensional. | ||
| Line 61: | Line 61: | ||
| <code>pml-layers</code> is a list of <code>pml</code> objects—you may have more than one <code>pml</code> object if you want PML layers only on certain sides of the cell, e.g. <code>(make pml (thickness 1.0) (direction X) (side High))</code> specifies a PML layer on only the <math>+x</math> side. Now, make an important point: the PML layer is ''inside'' the cell, overlapping whatever objects you have there. So, in this case our PML overlaps our waveguide, which is what we want so that it will properly absorb waveguide modes. The finite thickness of the PML is important to reduce numerical reflections; see [[perfectly matched layers]] for more information. | <code>pml-layers</code> is a list of <code>pml</code> objects—you may have more than one <code>pml</code> object if you want PML layers only on certain sides of the cell, e.g. <code>(make pml (thickness 1.0) (direction X) (side High))</code> specifies a PML layer on only the <math>+x</math> side. Now, make an important point: the PML layer is ''inside'' the cell, overlapping whatever objects you have there. So, in this case our PML overlaps our waveguide, which is what we want so that it will properly absorb waveguide modes. The finite thickness of the PML is important to reduce numerical reflections; see [[perfectly matched layers]] for more information. | ||
| - | Meep will discretize this structure in space and time, and that is specified by a single variable, <code>resolution</code>, that gives the number of pixels per distance unit. We'll set this resolution to 10, which corresponds to around 67 pixels/wavelength, or around 20 pixels/wavelength in the high-dielectric material. (n general, at least 8 pixels/wavelength in the highest dielectric is a good idea.) This will give us a <math>150\times80</math> cell. | + | Meep will discretize this structure in space and time, and that is specified by a single variable, <code>resolution</code>, that gives the number of pixels per distance unit. We'll set this resolution to 10, which corresponds to around 67 pixels/wavelength, or around 20 pixels/wavelength in the high-dielectric material. (n general, at least 8 pixels/wavelength in the highest dielectric is a good idea.) This will give us a <math>160\times80</math> cell. |
| (set! resolution 10) | (set! resolution 10) | ||
Revision as of 02:24, 27 October 2005
| Meep |
| Download |
| Release notes |
| FAQ |
| Meep manual |
| Introduction |
| Installation |
| Tutorial |
| Reference |
| C++ Tutorial |
| C++ Reference |
| Acknowledgements |
| License and Copyright |
In this page, we'll go through a couple of simple examples that illustrate the process of computing fields, transmission/reflection spectra, and resonant modes in Meep. Most of the examples here will be two-dimensinal calculations, simply because they are quicker than 3d computations and they illustrate all of the essential features.
This tutorial uses the libctl/Scheme scripting interface to Meep, which is what we expect most users to employ most of the time. There is also a C++ interface that may give additional flexibility in some situations; that is described in the C++ tutorial.
In order to convert the HDF5 output files of Meep into images of the fields and so on, this tutorial uses our free h5utils programs. (You could also use any other program, such as Matlab, that supports reading HDF5 files.)
Contents |
The ctl file
The use of Meep revolves around the control file, abbreviated "ctl" and typically called something like foo.ctl (although you can use any file name you wish). The ctl file specifies the geometry you wish to study, the current sources, the outputs computed, and everything else specific to your calculation. Rather than a flat, inflexible file format, however, the ctl file is actually written in a scripting language. This means that it can be everything from a simple sequence of commands setting the geometry, etcetera, to a full-fledged program with user input, loops, and anything else that you might need.
Don't worry, though—simple things are simple (you don't need to be a Real Programmer), and even there you will appreciate the flexibility that a scripting language gives you. (e.g. you can input things in any order, without regard for whitespace, insert comments where you please, omit things when reasonable defaults are available...)
The ctl file is actually implemented on top of the libctl library, a set of utilities that are in turn built on top of the Scheme language. Thus, there are three sources of possible commands and syntax for a ctl file:
- Scheme, a powerful and beautiful programming language developed at MIT, which has a particularly simple syntax: all statements are of the form
(function arguments...). We run Scheme under the GNU Guile interpreter (designed to be plugged into programs as a scripting and extension language). You don't need to know much Scheme for a basic ctl file, but it is always there if you need it; you can learn more about it from these Guile and Scheme links. - libctl, a library that we built on top of Guile to simplify communication between Scheme and scientific computation software. libctl sets the basic tone of the interface and defines a number of useful functions (such as multi-variable optimization, numeric integration, and so on). See the libctl manual pages.
- Meep itself, which defines all the interface features that are specific to FDTD calculations. This manual is primarily focused on documenting these features.
At this point, please take a moment to leaf through the libctl tutorial to get a feel for the basic style of the interface, before we get to the Meep-specific stuff below.
Okay, let's continue with our tutorial. The Meep program is normally invoked by running something like the following at the Unix command-line (herein denoted by the unix% prompt):
unix% meep foo.ctl >& foo.out
which reads the ctl file foo.ctl and executes it, saving the output to the file foo.out. However, if you invoke meep with no arguments, you are dropped into an interactive mode in which you can type commands and see their results immediately. If you do that now, you can paste in the commands from the tutorial as you follow it and see what they do.
Fields in a waveguide
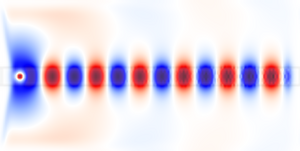
For our first example, let's examine the field pattern excited by a localized CW source in a waveguide— first straight, then bent. Our waveguide will have (non-dispersive) 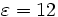 and width 1. That is, we pick units of length so that the width is 1, and define everything in terms of that (see also units in meep).
and width 1. That is, we pick units of length so that the width is 1, and define everything in terms of that (see also units in meep).
Before we define the structure, however, we have to define the computational cell. We're going to put a source at one end and watch it propagate down the waveguide in the x direction, so let's use a cell of length 15 in the x direction to give it some distance to propagate. In the y direction, we just need enough room so that the boundaries (below) don't affect the waveguide mode; let's give it a size of 8. We now specify these sizes in our ctl file via the geometry-lattice variable:
(set! geometry-lattice (make lattice (size 16 8 no-size)))
(The name geometry-lattice comes from MPB, where it can be used to define a more general periodic lattice. Although Meep supports periodic structures, it is less general than MPB in that affine grids are not supported.) set! is a Scheme command to set the value of an input variable. The last no-size parameter says that the computational cell has no size in the z direction, i.e. it is two-dimensional.
Now, we can add the waveguide. Most commonly, the structure is specified by a list of geometric objects, stored in the geometry variable. Here, we do:
(set! geometry (list
(make block (center 0 0) (size infinity 1 infinity)
(material (make dielectric (epsilon 12))))))
The waveguide is specified by a block (parallelepiped) of size 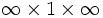 , with ε=12, centered at (0,0) (the center of the computational cell). By default, any place where there are no objects there is air (ε=1), although this can be changed by setting the
, with ε=12, centered at (0,0) (the center of the computational cell). By default, any place where there are no objects there is air (ε=1), although this can be changed by setting the default-material variable. The resulting structure is shown at right.
Now that we have the structure, we need to specify the current sources, which is specified as a list called sources of source objects. The simplest thing is to add a point source Jz:
(set! sources (list
(make source
(src (make continuous-src (frequency 0.15)))
(component Ez)
(center -7 0))))
Here, we gave the source a frequency of 0.15, and specified a continuous-src which is just a fixed-frequency sinusoid exp( − iωt) that (by default) is turned on at t = 0. Recall that, in Meep units, frequency is specified in units of 2πc, which is equivalent to the inverse of vacuum wavelength. Thus, 0.15 corresponds to a vacuum wavelength of about 6.67, or a wavelength of about 2 in the 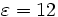 material—thus, our waveguide is half a wavelength wide, which should hopefully make it single-mode. (In fact, the cutoff for single-mode behavior in this waveguide is analytically solvable, and corresponds to a frequency of 1/2√11 or roughly 1.51.) Note also that to specify a Jz, we specify a component Ez (e.g. if we wanted a magnetic current, we would specify
material—thus, our waveguide is half a wavelength wide, which should hopefully make it single-mode. (In fact, the cutoff for single-mode behavior in this waveguide is analytically solvable, and corresponds to a frequency of 1/2√11 or roughly 1.51.) Note also that to specify a Jz, we specify a component Ez (e.g. if we wanted a magnetic current, we would specify Hx, Hy, or Hz). The current is located at ( − 7,0), which is 1 unit to the right of the left edge of the cell—we always want to leave a little space between sources and the cell boundaries, to keep the boundary conditions from interfering with them.
Speaking of boundary conditions, we want to add absorbing boundaries around our cell. Absorbing boundaries in Meep are handled by perfectly matched layers (PML)— which aren't really a boundary condition at all, but rather a fictitious absorbing material added around the edges of the cell. To add an absorbing layer of thickness 1 around all sides of the cell, we do:
(set! pml-layers (list (make pml (thickness 1.0))))
pml-layers is a list of pml objects—you may have more than one pml object if you want PML layers only on certain sides of the cell, e.g. (make pml (thickness 1.0) (direction X) (side High)) specifies a PML layer on only the + x side. Now, make an important point: the PML layer is inside the cell, overlapping whatever objects you have there. So, in this case our PML overlaps our waveguide, which is what we want so that it will properly absorb waveguide modes. The finite thickness of the PML is important to reduce numerical reflections; see perfectly matched layers for more information.
Meep will discretize this structure in space and time, and that is specified by a single variable, resolution, that gives the number of pixels per distance unit. We'll set this resolution to 10, which corresponds to around 67 pixels/wavelength, or around 20 pixels/wavelength in the high-dielectric material. (n general, at least 8 pixels/wavelength in the highest dielectric is a good idea.) This will give us a 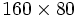 cell.
cell.
(set! resolution 10)
Now, we are ready to run the simulation! We do this by calling the run-until function. The first argument to run-until is the time to run for, and the subsequent arguments specify fields to output (or other kinds of analyses at each time step):
(run-until 200
(at-beginning output-epsilon)
(at-end output-efield-z))
Here, we are outputting the dielectric function ε and the electric-field component Ez, but have wrapped the output functions (which would otherwise run at every time step) in at-beginning and at-end, which do just what they say. There are several other such functions to modify the output behavior—and you can, of course, write your own, and in fact you can do any computation or output you want at any time during the time evolution (and even modify the simulation while it is running).
It should complete in a few seconds. If you are running interactively, the two output files will be called eps-000000.00.h5 and ez-000200.00.h5 (notice that the file names include the time at which they were output). If we were running a tutorial.ctl file, then the outputs will be tutorial-eps-000000.00.h5 and tutorial-ez-000200.00.h5. In any case, we can now analyze and visualize these files with a wide variety of programs that support the HDF5 format, including our own h5utils, and in particular the h5topng program to convert them to PNG images.
unix% h5topng -S3 eps-000000.00.h5
This will create eps-000000.00.png, where the -S3 increases the image scale by 3 (so that it is around 450 pixels wide, in this case). In fact, precisely this command is what created the dielectric image above. Much more interesting, however, are the fields:
unix% h5topng -S3 -Zc dkbluered -a yarg -A eps-000000.00.h5 ez-000200.00.h5
Briefly, the -Zc dkbluered makes the color scale go from dark blue (negative) to white (zero) to dark red (positive), and the -a/-A options overlay the dielectric function as light gray contours. This results in the image:
Here, we see that the the source has excited the waveguide mode, but has also excited radiating fields propagating away from the waveguide. At the boundaries, the field quickly goes to zero due to the PML layers.
Now, we'll start a new simulation where we look at the fields in a bent waveguide, and we'll do a couple of other things differently as well. If you are running Meep interactively, you will want to get rid of the old structure and fields so that Meep will re-initialize them:
(reset-meep)
Then let's set up the bent waveguide, in a slightly bigger computational cell, via:
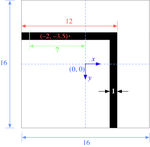
(set! geometry-lattice (make lattice (size 16 16 no-size)))
(set! geometry (list
(make block (center -2 -3.5) (size 12 1 infinity)
(material (make dielectric (epsilon 12))))
(make block (center 3.5 2) (size 1 12 infinity)
(material (make dielectric (epsilon 12))))))
(set! pml-layers (list (make pml (thickness 1.0))))
(set! resolution 10)
Note that we now have two blocks, both off-center to produce the bent waveguide structure pictured at right. Note that, by default, Meep uses periodic boundary conditions (in addition to the PML layers), so we see one pixel of dielectric "wrapped around" the edges from where the waveguide touches the boundary.
We also need to shift our source to y = − 4 so that it is still inside the waveguide. While we're at it, we'll make a couple of other changes. First, a point source does not couple very efficiently to the waveguide mode, so we'll expand this into a line source the same width as the waveguide by adding a size property to the source (a future version of Meep will allow you to use a current with the exact field pattern as computed by MPB). Second, instead of turning the source on suddenly at t = 0 (which excites many other frequencies because of the discontinuity), we will ramp it on slowly (technically, Meep uses a tanh turn-on function) over a time proportional to the width of 20 time units (a little over three periods). Finally, just for variety, we'll specify the (vacuum) wavelength instead of the frequency; again, we'll use a wavelength such that the waveguide is half a wavelength wide.
(set! sources (list
(make source
(src (make continuous-src
(wavelength (* 2 (sqrt 12))) (width 20)))
(component Ez)
(center -7 -3.5) (size 0 1))))
Finally, we'll run the simulation. Instead of running output-efield-z only at the end of the simulation, however, we'll run it at every 0.6 time units (about 10 times per period) via (at-every 0.6 output-efield-z). By itself, this would output a separate file for every different output time, but instead we'll use another feature of Meep to output to a single three-dimensional HDF5 file, where the third dimension is time:
(run-until 200
(at-beginning output-epsilon)
(to-appended "ez" (at-every 0.6 output-efield-z)))
Here, "ez" determines the name of the output file, which will be called ez.h5 if you are running interactively or will be prefixed with the name of the file name for a ctl file (e.g. tutorial-ez.h5 for tutorial.ctl). If we run h5ls on this file (a standard utility, included with HDF5, that lists the contents of the HDF5 file), we get:
unix% h5ls ez.h5
ez Dataset {161, 161, 330/Inf}
That is, the file contains a single dataset ez that is a 162×162×330 array, where the last dimension is time. (This is rather a large file, 69MB; later, we'll see ways to reduce this size if we only want images.) Now, we have a number of choices of how to output the fields. To output a single time slice, we can use the same h5topng command as before, but with an additional -t option to specify the time index: e.g. h5topng -t 229 will output the last time slice, similar to before. Instead, let's create an animation of the fields as a function of time. First, we have to create images for all of the time slices:
unix% h5topng -t 0:329 -R -Zc dkbluered -a yarg -A eps-000000.00.h5 ez.h5
This is similar to the command before, with two new options: -t 0:329 outputs images for all time indices from 0 to 329, i.e. all of the times, and the the -R flag tells h5topng to use a consistent color scale for every image (instead of scaling each image independently). Then, we have to convert these images into an animation in some format. For this, we'll use the free ImageMagick convert program (although there is other software that will do the trick as well).
unix% convert ez.t*.png ez.gif
Here, we are using an animated GIF format for the output, which is not the most efficient animation format (e.g. ez.mpg, for MPEG format, would be better), but it is unfortunately the only format supported by this Wiki software. This results in the following animation :
It is clear that the transmission around the bend is rather low for this frequency and structure—both large reflection and large radiation loss are clearly visible. Moreover, since we operating are just barely below the cutoff for single-mode behavior, we are able to excite a second leaky mode after the waveguide bend, whose second-order mode pattern (superimposed with the fundamental mode) is apparent in the animation. At right, we show a field snapshot from a simulation with a larger cell along the y direction, in which you can see that the second-order leaky mode decays away, leaving us with the fundamental mode propagating downward.
Instead of doing an animation, another interesting possibility is to make an image from a  slice. Here is the y = − 3.5 slice, which gives us an image of the fields in the first waveguide branch as a function of time.
slice. Here is the y = − 3.5 slice, which gives us an image of the fields in the first waveguide branch as a function of time.
unix% h5topng -0y -35 -Zc dkbluered ez.h5
Here, the -0y -35 specifies the y = − 3.5 slice, where we have multiplied by 10 (our resolution) to get the pixel coordinate.
Transmission spectrum around a waveguide bend
A resonant mode
More examples
emacs and ctl
It is useful to have emacs use its scheme-mode for editing ctl files, so that hitting tab indents nicely, and so on. emacs does this automatically for files ending with ".scm"; to do it for files ending with ".ctl" as well, add the following lines to your ~/.emacs file:
(push '("\\.ctl\\'" . scheme-mode) auto-mode-alist)
or if your emacs version is 24.3 or earlier and you have other ".ctl" files which are not Scheme:
(if (assoc "\\.ctl" auto-mode-alist)
nil
(add-to-list 'auto-mode-alist '("\\.ctl\\'" . scheme-mode))))
(Incidentally, emacs scripts are written in "elisp," a language closely related to Scheme.)
If you don't use emacs (or derivatives such as Aquamacs), it would be good to find another editor that supports a Scheme mode. For example, jEdit is a free/open-source cross-platform editor with Scheme-syntax support. Another option is GNU gedit (for GNU/Linux and Unix); in fact, S. Hessam Moosavi Mehr has donated a hilighting mode for Meep/MPB that specially highlights the Meep/MPB keywords.