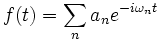Meep Tutorial
From AbInitio
| Revision as of 06:38, 4 November 2005 (edit) Stevenj (Talk | contribs) (→A resonant mode) ← Previous diff |
Revision as of 06:45, 4 November 2005 (edit) Stevenj (Talk | contribs) (→A resonant mode) Next diff → |
||
| Line 312: | Line 312: | ||
| ==A resonant mode== | ==A resonant mode== | ||
| - | As described in the [[Meep Introduction#Resonant modes|Meep introduction]], another common task for FDTD simulation is to find the resonant modes—frequencies and decay rates—of some electromagnetic cavity structure. (You might want to read that introduction again to recall the basic computational strategy.) Here, we will show how this works for perhaps the simplest example of a dielectric cavity: a '''ring resonator''', which is simply a waveguide bent into a circle. (This can be also found in the <code>examples/tut-ring.ctl</code> file included with Meep.) | + | As described in the [[Meep Introduction#Resonant modes|Meep introduction]], another common task for FDTD simulation is to find the resonant modes—frequencies and decay rates—of some electromagnetic cavity structure. (You might want to read that introduction again to recall the basic computational strategy.) Here, we will show how this works for perhaps the simplest example of a dielectric cavity: a '''ring resonator''', which is simply a waveguide bent into a circle. (This can be also found in the <code>examples/tut-ring.ctl</code> file included with Meep.) In fact, since this structure has cylindrical symmetry, we can simulate it ''much'' more efficiently [[Meep Tutorial/Ring resonator in cylindrical coordinates|by using cylindrical coordinates]], but for illustration we'll just use an ordinary 2d simulation. |
| As before, we'll define some parameters to describe the geometry, so that we can easily change the structure: | As before, we'll define some parameters to describe the geometry, so that we can easily change the structure: | ||
| Line 392: | Line 392: | ||
| |[[Image:Tut-ring-ez-0.175.gif|center|ω=0.175 mode]] | |[[Image:Tut-ring-ez-0.175.gif|center|ω=0.175 mode]] | ||
| |} | |} | ||
| + | |||
| + | (Each of these modes is, of course, doubly-degenerate according to the representations of the <math>C_{\infty\mathrm{v}}</math> symmetry group. The other mode is simply a slight rotation of this mode to make it ''odd'' through the <math>x</math> axis, whereas we excited only the ''even'' modes due to our source symmetry.) | ||
| You may have noticed, by the way, that when you run with the narrow-bandwidth source, <code>harminv</code> gives you slightly different frequency and <math>Q</math> estimates, with a much smaller error estimate—this is not too strange, since by exciting a single mode you generate a cleaner signal that can be analyzed more accurately. For example, the narrow-bandwidth source for the <math>\omega=0.175</math> mode gives: | You may have noticed, by the way, that when you run with the narrow-bandwidth source, <code>harminv</code> gives you slightly different frequency and <math>Q</math> estimates, with a much smaller error estimate—this is not too strange, since by exciting a single mode you generate a cleaner signal that can be analyzed more accurately. For example, the narrow-bandwidth source for the <math>\omega=0.175</math> mode gives: | ||
| Line 398: | Line 400: | ||
| which differs by about 0.00001 (<math>10^{-5}</math>) from the earlier estimate; the difference in <math>Q</math> is, of course, larger because a small absolute error in <math>\omega</math> gives a larger relative error in the small imaginary frequency. | which differs by about 0.00001 (<math>10^{-5}</math>) from the earlier estimate; the difference in <math>Q</math> is, of course, larger because a small absolute error in <math>\omega</math> gives a larger relative error in the small imaginary frequency. | ||
| + | |||
| + | See also: [[Meep Tutorial/Ring resonator in cylindrical coordinates|Ring resonator in cylindrical coordinates]] for how to solve this cylindrical geometry much more efficiently. | ||
| ==More examples== | ==More examples== | ||
Revision as of 06:45, 4 November 2005
| Meep |
| Download |
| Release notes |
| FAQ |
| Meep manual |
| Introduction |
| Installation |
| Tutorial |
| Reference |
| C++ Tutorial |
| C++ Reference |
| Acknowledgements |
| License and Copyright |
In this page, we'll go through a couple of simple examples that illustrate the process of computing fields, transmission/reflection spectra, and resonant modes in Meep. Most of the examples here will be two-dimensinal calculations, simply because they are quicker than 3d computations and they illustrate all of the essential features.
This tutorial uses the libctl/Scheme scripting interface to Meep, which is what we expect most users to employ most of the time. There is also a C++ interface that may give additional flexibility in some situations; that is described in the C++ tutorial.
In order to convert the HDF5 output files of Meep into images of the fields and so on, this tutorial uses our free h5utils programs. (You could also use any other program, such as Matlab, that supports reading HDF5 files.)
Contents |
The ctl file
The use of Meep revolves around the control file, abbreviated "ctl" and typically called something like foo.ctl (although you can use any file name you wish). The ctl file specifies the geometry you wish to study, the current sources, the outputs computed, and everything else specific to your calculation. Rather than a flat, inflexible file format, however, the ctl file is actually written in a scripting language. This means that it can be everything from a simple sequence of commands setting the geometry, etcetera, to a full-fledged program with user input, loops, and anything else that you might need.
Don't worry, though—simple things are simple (you don't need to be a Real Programmer), and even there you will appreciate the flexibility that a scripting language gives you. (e.g. you can input things in any order, without regard for whitespace, insert comments where you please, omit things when reasonable defaults are available...)
The ctl file is actually implemented on top of the libctl library, a set of utilities that are in turn built on top of the Scheme language. Thus, there are three sources of possible commands and syntax for a ctl file:
- Scheme, a powerful and beautiful programming language developed at MIT, which has a particularly simple syntax: all statements are of the form
(function arguments...). We run Scheme under the GNU Guile interpreter (designed to be plugged into programs as a scripting and extension language). You don't need to know much Scheme for a basic ctl file, but it is always there if you need it; you can learn more about it from these Guile and Scheme links. - libctl, a library that we built on top of Guile to simplify communication between Scheme and scientific computation software. libctl sets the basic tone of the interface and defines a number of useful functions (such as multi-variable optimization, numeric integration, and so on). See the libctl manual pages.
- Meep itself, which defines all the interface features that are specific to FDTD calculations. This manual is primarily focused on documenting these features.
At this point, please take a moment to leaf through the libctl tutorial to get a feel for the basic style of the interface, before we get to the Meep-specific stuff below. (If you've used MPB, all of this stuff should already be familiar, although Meep is somewhat more complex because it can perform a wider variety of computations.)
Okay, let's continue with our tutorial. The Meep program is normally invoked by running something like the following at the Unix command-line (herein denoted by the unix% prompt):
unix% meep foo.ctl >& foo.out
which reads the ctl file foo.ctl and executes it, saving the output to the file foo.out. However, if you invoke meep with no arguments, you are dropped into an interactive mode in which you can type commands and see their results immediately. If you do that now, you can paste in the commands from the tutorial as you follow it and see what they do.
Fields in a waveguide
For our first example, let's examine the field pattern excited by a localized CW source in a waveguide— first straight, then bent. Our waveguide will have (non-dispersive) 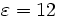 and width 1. That is, we pick units of length so that the width is 1, and define everything in terms of that (see also units in meep).
and width 1. That is, we pick units of length so that the width is 1, and define everything in terms of that (see also units in meep).
A straight waveguide
Before we define the structure, however, we have to define the computational cell. We're going to put a source at one end and watch it propagate down the waveguide in the x direction, so let's use a cell of length 16 in the x direction to give it some distance to propagate. In the y direction, we just need enough room so that the boundaries (below) don't affect the waveguide mode; let's give it a size of 8. We now specify these sizes in our ctl file via the geometry-lattice variable:
(set! geometry-lattice (make lattice (size 16 8 no-size)))
(The name geometry-lattice comes from MPB, where it can be used to define a more general periodic lattice. Although Meep supports periodic structures, it is less general than MPB in that affine grids are not supported.) set! is a Scheme command to set the value of an input variable. The last no-size parameter says that the computational cell has no size in the z direction, i.e. it is two-dimensional.
Now, we can add the waveguide. Most commonly, the structure is specified by a list of geometric objects, stored in the geometry variable. Here, we do:
(set! geometry (list
(make block (center 0 0) (size infinity 1 infinity)
(material (make dielectric (epsilon 12))))))
The waveguide is specified by a block (parallelepiped) of size 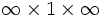 , with ε=12, centered at (0,0) (the center of the computational cell). By default, any place where there are no objects there is air (ε=1), although this can be changed by setting the
, with ε=12, centered at (0,0) (the center of the computational cell). By default, any place where there are no objects there is air (ε=1), although this can be changed by setting the default-material variable. The resulting structure is shown at right.
Now that we have the structure, we need to specify the current sources, which is specified as a list called sources of source objects. The simplest thing is to add a point source Jz:
(set! sources (list
(make source
(src (make continuous-src (frequency 0.15)))
(component Ez)
(center -7 0))))
Here, we gave the source a frequency of 0.15, and specified a continuous-src which is just a fixed-frequency sinusoid exp( − iωt) that (by default) is turned on at t = 0. Recall that, in Meep units, frequency is specified in units of 2πc, which is equivalent to the inverse of vacuum wavelength. Thus, 0.15 corresponds to a vacuum wavelength of about 1 / 0.15 = 6.67, or a wavelength of about 2 in the 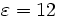 material—thus, our waveguide is half a wavelength wide, which should hopefully make it single-mode. (In fact, the cutoff for single-mode behavior in this waveguide is analytically solvable, and corresponds to a frequency of 1/2√11 or roughly 0.15076.) Note also that to specify a Jz, we specify a component Ez (e.g. if we wanted a magnetic current, we would specify
material—thus, our waveguide is half a wavelength wide, which should hopefully make it single-mode. (In fact, the cutoff for single-mode behavior in this waveguide is analytically solvable, and corresponds to a frequency of 1/2√11 or roughly 0.15076.) Note also that to specify a Jz, we specify a component Ez (e.g. if we wanted a magnetic current, we would specify Hx, Hy, or Hz). The current is located at ( − 7,0), which is 1 unit to the right of the left edge of the cell—we always want to leave a little space between sources and the cell boundaries, to keep the boundary conditions from interfering with them.
Speaking of boundary conditions, we want to add absorbing boundaries around our cell. Absorbing boundaries in Meep are handled by perfectly matched layers (PML)— which aren't really a boundary condition at all, but rather a fictitious absorbing material added around the edges of the cell. To add an absorbing layer of thickness 1 around all sides of the cell, we do:
(set! pml-layers (list (make pml (thickness 1.0))))
pml-layers is a list of pml objects—you may have more than one pml object if you want PML layers only on certain sides of the cell, e.g. (make pml (thickness 1.0) (direction X) (side High)) specifies a PML layer on only the + x side. Now, make an important point: the PML layer is inside the cell, overlapping whatever objects you have there. So, in this case our PML overlaps our waveguide, which is what we want so that it will properly absorb waveguide modes. The finite thickness of the PML is important to reduce numerical reflections; see perfectly matched layers for more information.
Meep will discretize this structure in space and time, and that is specified by a single variable, resolution, that gives the number of pixels per distance unit. We'll set this resolution to 10, which corresponds to around 67 pixels/wavelength, or around 20 pixels/wavelength in the high-dielectric material. (n general, at least 8 pixels/wavelength in the highest dielectric is a good idea.) This will give us a 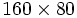 cell.
cell.
(set! resolution 10)
Now, we are ready to run the simulation! We do this by calling the run-until function. The first argument to run-until is the time to run for, and the subsequent arguments specify fields to output (or other kinds of analyses at each time step):
(run-until 200
(at-beginning output-epsilon)
(at-end output-efield-z))
Here, we are outputting the dielectric function ε and the electric-field component Ez, but have wrapped the output functions (which would otherwise run at every time step) in at-beginning and at-end, which do just what they say. There are several other such functions to modify the output behavior—and you can, of course, write your own, and in fact you can do any computation or output you want at any time during the time evolution (and even modify the simulation while it is running).
It should complete in a few seconds. If you are running interactively, the two output files will be called eps-000000.00.h5 and ez-000200.00.h5 (notice that the file names include the time at which they were output). If we were running a tutorial.ctl file, then the outputs will be tutorial-eps-000000.00.h5 and tutorial-ez-000200.00.h5. In any case, we can now analyze and visualize these files with a wide variety of programs that support the HDF5 format, including our own h5utils, and in particular the h5topng program to convert them to PNG images.
unix% h5topng -S3 eps-000000.00.h5
This will create eps-000000.00.png, where the -S3 increases the image scale by 3 (so that it is around 450 pixels wide, in this case). In fact, precisely this command is what created the dielectric image above. Much more interesting, however, are the fields:
unix% h5topng -S3 -Zc dkbluered -a yarg -A eps-000000.00.h5 ez-000200.00.h5
Briefly, the -Zc dkbluered makes the color scale go from dark blue (negative) to white (zero) to dark red (positive), and the -a/-A options overlay the dielectric function as light gray contours. This results in the image:
Here, we see that the the source has excited the waveguide mode, but has also excited radiating fields propagating away from the waveguide. At the boundaries, the field quickly goes to zero due to the PML layers. If we look carefully (click on the image to see a larger view), we see somethinge else—the image is "speckled" towards the right side. This is because, by turning on the current abruptly at t = 0, we have excited high-frequency components (very high order modes), and we have not waited long enough for them to die away; we'll eliminate these in the next section by turning on the source more smoothly.
A 90° bend
Now, we'll start a new simulation where we look at the fields in a bent waveguide, and we'll do a couple of other things differently as well. If you are running Meep interactively, you will want to get rid of the old structure and fields so that Meep will re-initialize them:
(reset-meep)
Then let's set up the bent waveguide, in a slightly bigger computational cell, via:
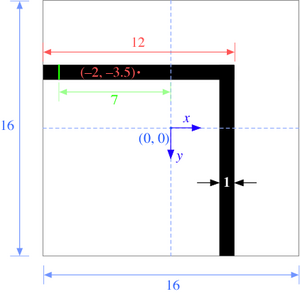
(set! geometry-lattice (make lattice (size 16 16 no-size)))
(set! geometry (list
(make block (center -2 -3.5) (size 12 1 infinity)
(material (make dielectric (epsilon 12))))
(make block (center 3.5 2) (size 1 12 infinity)
(material (make dielectric (epsilon 12))))))
(set! pml-layers (list (make pml (thickness 1.0))))
(set! resolution 10)
Note that we now have two blocks, both off-center to produce the bent waveguide structure pictured at right. As illustrated in the figure, the origin (0,0) of the coordinate system is at the center of the computational cell, with positive y being downwards in h5topng, and thus the block of size 12×1 is centered at ( − 2, − 3.5). Also shown in green is the source plane at x = − 7 (see below).
We also need to shift our source to y = − 3.5 so that it is still inside the waveguide. While we're at it, we'll make a couple of other changes. First, a point source does not couple very efficiently to the waveguide mode, so we'll expand this into a line source the same width as the waveguide by adding a size property to the source (a future version of Meep will allow you to use a current with the exact field pattern as computed by MPB). Second, instead of turning the source on suddenly at t = 0 (which excites many other frequencies because of the discontinuity), we will ramp it on slowly (technically, Meep uses a tanh turn-on function) over a time proportional to the width of 20 time units (a little over three periods). Finally, just for variety, we'll specify the (vacuum) wavelength instead of the frequency; again, we'll use a wavelength such that the waveguide is half a wavelength wide.
(set! sources (list
(make source
(src (make continuous-src
(wavelength (* 2 (sqrt 12))) (width 20)))
(component Ez)
(center -7 -3.5) (size 0 1))))
Finally, we'll run the simulation. Instead of running output-efield-z only at the end of the simulation, however, we'll run it at every 0.6 time units (about 10 times per period) via (at-every 0.6 output-efield-z). By itself, this would output a separate file for every different output time, but instead we'll use another feature of Meep to output to a single three-dimensional HDF5 file, where the third dimension is time:
(run-until 200
(at-beginning output-epsilon)
(to-appended "ez" (at-every 0.6 output-efield-z)))
Here, "ez" determines the name of the output file, which will be called ez.h5 if you are running interactively or will be prefixed with the name of the file name for a ctl file (e.g. tutorial-ez.h5 for tutorial.ctl). If we run h5ls on this file (a standard utility, included with HDF5, that lists the contents of the HDF5 file), we get:
unix% h5ls ez.h5
ez Dataset {161, 161, 330/Inf}
That is, the file contains a single dataset ez that is a 162×162×330 array, where the last dimension is time. (This is rather a large file, 69MB; later, we'll see ways to reduce this size if we only want images.) Now, we have a number of choices of how to output the fields. To output a single time slice, we can use the same h5topng command as before, but with an additional -t option to specify the time index: e.g. h5topng -t 229 will output the last time slice, similar to before. Instead, let's create an animation of the fields as a function of time. First, we have to create images for all of the time slices:
unix% h5topng -t 0:329 -R -Zc dkbluered -a yarg -A eps-000000.00.h5 ez.h5
This is similar to the command before, with two new options: -t 0:329 outputs images for all time indices from 0 to 329, i.e. all of the times, and the the -R flag tells h5topng to use a consistent color scale for every image (instead of scaling each image independently). Then, we have to convert these images into an animation in some format. For this, we'll use the free ImageMagick convert program (although there is other software that will do the trick as well).
unix% convert ez.t*.png ez.gif
Here, we are using an animated GIF format for the output, which is not the most efficient animation format (e.g. ez.mpg, for MPEG format, would be better), but it is unfortunately the only format supported by this Wiki software. This results in the following animation :
It is clear that the transmission around the bend is rather low for this frequency and structure—both large reflection and large radiation loss are clearly visible. Moreover, since we operating are just barely below the cutoff for single-mode behavior, we are able to excite a second leaky mode after the waveguide bend, whose second-order mode pattern (superimposed with the fundamental mode) is apparent in the animation. At right, we show a field snapshot from a simulation with a larger cell along the y direction, in which you can see that the second-order leaky mode decays away, leaving us with the fundamental mode propagating downward.
Instead of doing an animation, another interesting possibility is to make an image from a  slice. Here is the y = − 3.5 slice, which gives us an image of the fields in the first waveguide branch as a function of time.
slice. Here is the y = − 3.5 slice, which gives us an image of the fields in the first waveguide branch as a function of time.
unix% h5topng -0y -35 -Zc dkbluered ez.h5
Here, the -0y -35 specifies the y = − 3.5 slice, where we have multiplied by 10 (our resolution) to get the pixel coordinate.
Smaller files
Above, we outputted the full 2d data slice at every 0.6 time units, resulting in a 69MB file. This is not too bad by today's standards, but you can imagine how big the output file would get if we were doing a 3d simulation, or even a larger 2d simulation—one can easily generate gigabytes of files, which is not only wasteful but is also slow. Instead, it is possible to output more efficiently if you know what you want to look at.
To create the movie above, all we really need are the images corresponding to each time. Images can be stored much more efficiently than raw arrays of numbers—to exploit this fact, Meep allows you to output PNG images instead of HDF5 files. In particular, instead of output-efield-z as above, we can use (output-png Ez "-Zc dkbluered"), where Ez is the component to output and the "-Zc dkbluered" are options for h5topng (which is the program that is actually used to create the image files). That is:
(run-until 200 (at-every 0.6 (output-png Ez "-Zc bluered")))
will output a PNG file file every 0.6 time units, which can then be combined with convert as above to create a movie. The movie will be similar to the one before, but not identical because of how the color scale is determined. Before, we used the -R option to make h5topng use a uniform color scale for all images, based on the minimum/maximum field values over all time steps. That is not possible, here, because we output an image before knowing the field values at future time steps. Thus, what output-png does is to set its color scale based on the minimum/maximum field values from all past times—therefore, the color scale will slowly "ramp up" as the source turns on.
What if we want to output an  slice, as above? To do this, we only really wanted the values at y = − 3.5, and therefore we can exploit another powerful Meep output feature—Meep allows us to output only a subset of the computational cell. This is done using the
slice, as above? To do this, we only really wanted the values at y = − 3.5, and therefore we can exploit another powerful Meep output feature—Meep allows us to output only a subset of the computational cell. This is done using the in-volume function, which (like at-every and to-appended) is another function that modifies the behavior of other output functions. In particular, we can do:
(run-until 200
(to-appended "ez-slice"
(at-every 0.6
(in-volume (volume (center 0 -3.5) (size 16 0))
output-efield-z))))
The first argument to in-volume is a volume, specified by (volume (center ...) (size ...)), which applies to all of the nested output functions. (Note that to-appended, at-every, and in-volume are cumulative regardless of what order you put them in.) This creates the output file ez-slice.h5 which contains a dataset of size 162×330 corresponding to the desired  slice.
slice.
Transmission spectrum around a waveguide bend
Above, we computed the field patterns for light propagating around a waveguide bend. While this is pretty, the results are not quantitatively satisfying. We'd like to know exactly how much power makes it around the bend, how much is reflected, and how much is radiated away. How can we do this?
The basic principles were described in the Meep introduction; please re-read that section if you have forgotten. Basically, we'll tell Meep to keep track of the fields and their Fourier transforms in a certain region, and from this compute the flux of electromagnetic energy as a function of ω. Moreover, we'll get an entire spectrum of the transmission in a single run, by Fourier-transforming the response to a short pulse. However, in order to normalize the transmission (to get transmission as a fraction of incident power), we'll have to do two runs, one with and one without a bend.
This control file will be more complicated than before, so you'll definitely want it as a separate file rather than typing it interactively. See the tut-bend-flux.ctl file included with Meep in its examples/ directory.
Above, we hard-coded all of the parameters like the cell size, the waveguide width, etcetera. For serious work, however, this is inefficient—we often want to explore many different values of such parameters. For example, we may want to change the size of the cell, so we'll define it as:
(define-param sx 16) ; size of cell in X direction (define-param sy 32) ; size of cell in Y direction (set! geometry-lattice (make lattice (size sx sy no-size)))
(Notice that a semicolon ";" begins a comment, which is ignored by Meep.) define-param is a libctl feature to define variables that can be overridden from the command line. We could now do meep sx=17 tut-wvg-bend-trans.ctl to change the X size to 17, without editing the ctl file, for example. We'll also define a couple of parameters to set the width of the waveguide and the "padding" between it and the edge of the computational cell:
(define-param pad 4) ; padding distance between waveguide and cell edge (define-param w 1) ; width of waveguide
In order to define the waveguide positions, etcetera, we will now have to use arithmetic. For example, the y center of the horizontal waveguide will be given by -0.5 * (sy - w - 2*pad). At least, that is what the expression would look like in C; in Scheme, the syntax for 1 + 2 is (+ 1 2), and so on, so we will define the vertical and horizontal waveguide centers as:
(define wvg-ycen (* -0.5 (- sy w (* 2 pad)))) ; y center of horiz. wvg (define wvg-xcen (* 0.5 (- sx w (* 2 pad)))) ; x center of vert. wvg
Now, we have to make the geometry, as before. This time, however, we really want two geometries: the bend, and also a straight waveguide for normalization. We could do this with two separate ctl files, but that is annoying. Instead, we'll define a parameter no-bend? which is true for the straight-waveguide case and false for the bend.
(define-param no-bend? false) ; if true, have straight waveguide, not bend
Now, we define the geometry via two cases, with an if statement—the Scheme syntax is (if predicate? if-true if-false).
(set! geometry
(if no-bend?
(list
(make block
(center 0 wvg-ycen)
(size infinity w infinity)
(material (make dielectric (epsilon 12)))))
(list
(make block
(center (* -0.5 pad) wvg-ycen)
(size (- sx pad) w infinity)
(material (make dielectric (epsilon 12))))
(make block
(center wvg-xcen (* 0.5 pad))
(size w (- sy pad) infinity)
(material (make dielectric (epsilon 12)))))))
Thus, if no-bend? is true we make a single block for a straight waveguide, and otherwise we make two blocks for a bent waveguide.
The source is now a gaussian-src instead of a continuous-src, parameterized by a center frequency and a frequency width (the width of the Gaussian spectrum), which we'll define via define-param as usual.
(define-param fcen 0.15) ; pulse center frequency
(define-param df 0.1) ; pulse width (in frequency)
(set! sources (list
(make source
(src (make gaussian-src (frequency fcen) (fwidth df)))
(component Ez)
(center (+ 1 (* -0.5 sx)) wvg-ycen)
(size 0 w))))
Notice how we're using our parameters like wvg-ycen and w: if we change the dimensions, everythign will now shift automatically. The boundary conditions and resolution are set as before, except that now we'll use set-param! so that we can override the resolution from the command line.:
(set! pml-layers (list (make pml (thickness 1.0)))) (set-param! resolution 10)
Finally, we have to specify where we want Meep to compute the flux spectra, and at what frequencies. (This must be done after specifying the geometry, sources, resolution, etcetera, because all of the field parameters are initialized when flux planes are created.)
(define-param nfreq 100) ; number of frequencies at which to compute flux
(define trans ; transmitted flux
(add-flux fcen df nfreq
(if no-bend?
(make flux-region
(center (- (/ sx 2) 1.5) wvg-ycen) (size 0 (* w 2)))
(make flux-region
(center wvg-xcen (- (/ sy 2) 1.5)) (size (* w 2) 0)))))
(define refl ; reflected flux
(add-flux fcen df nfreq
(make flux-region
(center (+ (* -0.5 sx) 1.5) wvg-ycen) (size 0 (* w 2)))))
We compute the fluxes through a line segment twice the width of the waveguide, located at the beginning or end of the waveguide. (Note that the flux lines are separated by 1 from the boundary of the cell, so that they do not lie within the absorbing PML regions.) Again, there are two cases: the transmitted flux is either computed at the right or the bottom of the computational cell, depending on whether the waveguide is straight or bent.
Here, the fluxes will be computed for 100 (nfreq) frequencies centered on fcen, from fcen-df/2 to fcen+df/2. That is, we only compute fluxes for frequencies within our pulse bandwidth. This is important because, to far outside the pulse bandwidth, the spectral power is so low that numerical errors make the computed fluxes useless.
Now, as described in the Meep introduction, computing reflection spectra is a bit tricky because we need to separate the incident and reflected fields. We do this in Meep by saving the Fourier-transformed fields from the normalization run (no-bend?=true), and loading them, negated, before the other runs. The latter subtracts the Fourier-transformed incident fields from the Fourier transforms of the scattered fields; logically, we might subtract these after the run, but it turns out to be more convenient to subtract the incident fields first and then accumulate the Fourier transform. All of this is accomplished with two commands, save-flux (after the normalization run) and load-minus-flux (before the other runs). We can call them as follows:
(if (not no-bend?) (load-minus-flux "refl-flux" refl)) (run-sources+ 500 (at-beginning output-epsilon)) (if no-bend? (save-flux "refl-flux" refl))
This uses a file called refl-flux.h5, or actually tut-bend-flux-refl-flux.h5 (the ctl file name is used as a prefix) to store/load the Fourier transformed fields in the flux planes. The (run-sources+ 500) runs the simulation until the Gaussian source has turned off (which is done automatically once it has decayed for a few standard deviations), plus an additional 500 time units.
Why do we keep running after the source has turned off? Because we must give the pulse time to propagate completely across the cell. Moreover, the time required is a bit tricky to predict when you have complex structures, because there might be resonant phenomena that allow the source to bounce around for a long time. Therefore, it is convenient to specify the run time in a different way: instead of using a fixed time, we require that the | Ez | 2 at the end of the waveguide must have decayed by a given amount (e.g. 1/1000) from its peak value. We can do this via:
(run-sources+
(stop-when-fields-decayed 50 Ez
(if no-bend?
(vector3 (- (/ sx 2) 1.5) wvg-ycen)
(vector3 wvg-xcen (- (/ sy 2) 1.5)))
1e-3))
stop-when-fields-decayed takes three arguments: (stop-when-fields-decayed dT component pt decay-by). What it does is, after the sources have turned off, it keeps running for an additional dT time units every time the given |component|2 at the given point has not decayed by at least decay-by from its peak value for all times within the previous dT. In this case, dT=50, the component is Ez, the point is at the center of the flux plane at the end of the waveguide, and decay-by=0.001. So, it keeps running for an additional 50 time units until the square amplitude has decayed by 1/1000 from its peak: this should be sufficient to ensure that the Fourier transforms have converged.
Finally, we have to output the flux values:
(display-fluxes trans refl)
This prints a series of outputs like:
flux1:, 0.1, 7.91772317108475e-7, -3.16449591437196e-7 flux1:, 0.101010101010101, 1.18410865137737e-6, -4.85527604203706e-7 flux1:, 0.102020202020202, 1.77218779386503e-6, -7.37944901819701e-7 flux1:, 0.103030303030303, 2.63090852112034e-6, -1.11118350510327e-6 flux1:, ...
This is comma-delimited data, which can easily be imported into any spreadsheet or plotting program (e.g. Matlab): the first column is the frequency, the second is the transmitted power, and the third is the reflected power.
Now, we need to run the simulation twice, once with no-bend?=true and once with no-bend?=false (the default):
unix% meep no-bend?=true tut-bend-flux.ctl | tee bend0.out unix% meep tut-bend-flux.ctl | tee bend.out
(The tee command is a useful Unix command that saves the output to a file and displays it on the screen, so that we can see what is going on as it runs.) Then, we should pull out the flux1 lines into a separate file to import them into our plotting program:
unix% grep flux1: bend0.out > bend0.dat unix% grep flux1: bend.out > bend.dat
Now, we import them, and plot the results:
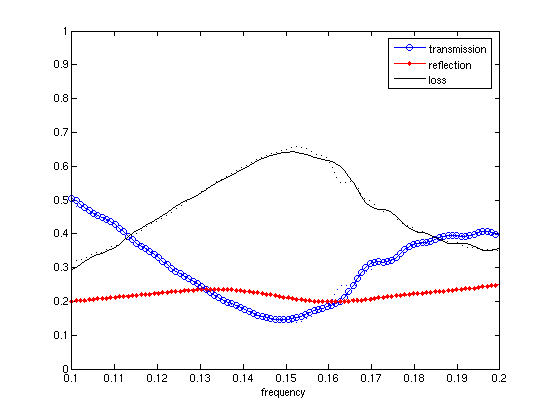
What are we plotting here? The transmission is the transmitted flux (second column of bend.dat) divided by the incident flux (second column of bend0.dat), to give us the fraction of power transmitted. The reflection is the reflected flux (third column of bend.dat) divided by the incident flux (second column of bend0.dat); we also have to multiply by − 1 because all fluxes in Meep are computed in the positive-coordinate direction by default, and we want the flux in the − x direction. Finally, the loss is simply 1 - transmission - reflection.
We should also check whether our data is converged, by increasing the resolution and cell size and seeing by how much the numbers change. In this case, we'll just try doubling the cell size:
unix% meep sx=32 sy=64 no-bend?=true tut-bend-flux.ctl |tee bend0-big.out unix% meep sx=32 sy=64 tut-bend-flux.ctl |tee bend-big.out
Again, we must run both simulations in order to get the normalization right. The results are included in the plot above as dotted lines—you can see that the numbers have changed slightly for transmission and loss, probably stemming from interference between light radiated directly from the source and light propagating around the waveguide. To be really confident, we should probably run the simulation again with an even bigger cell, but we'll call it enough for this tutorial.
A resonant mode
As described in the Meep introduction, another common task for FDTD simulation is to find the resonant modes—frequencies and decay rates—of some electromagnetic cavity structure. (You might want to read that introduction again to recall the basic computational strategy.) Here, we will show how this works for perhaps the simplest example of a dielectric cavity: a ring resonator, which is simply a waveguide bent into a circle. (This can be also found in the examples/tut-ring.ctl file included with Meep.) In fact, since this structure has cylindrical symmetry, we can simulate it much more efficiently by using cylindrical coordinates, but for illustration we'll just use an ordinary 2d simulation.
As before, we'll define some parameters to describe the geometry, so that we can easily change the structure:
(define-param n 3.4) ; index of waveguide (define-param w 1) ; width of waveguide (define-param r 1) ; inner radius of ring (define-param pad 4) ; padding between waveguide and edge of PML (define-param dpml 2) ; thickness of PML (define sxy (* 2 (+ r w pad dpml))) ; cell size (set! geometry-lattice (make lattice (size sxy sxy no-size)))
How do we make a circular waveguide? So far, we've only seen block objects, but Meep also lets you specify cylinders, spheres, ellipsoids, and cones, as well as user-specified dielectric functions. In this case, we'll use two cylinder objects, one inside the other:
(set! geometry (list
(make cylinder (center 0 0) (height infinity)
(radius (+ r w)) (material (make dielectric (index n))))
(make cylinder (center 0 0) (height infinity)
(radius r) (material air))))
(set! pml-layers (list (make pml (thickness dpml))))
(set-param! resolution 10)
Later objects in the geometry list take precedence over (lie "on top of") earlier objects, so the second air (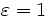 ) cylinder cuts a circular hole out of the larger cylinder, leaving a ring of width
) cylinder cuts a circular hole out of the larger cylinder, leaving a ring of width w.
Now, we don't know the frequency of the mode(s) ahead of time, so we'll just hit the structure with a broad Gaussian pulse to excite all of the (TM polarized) modes in a chosen bandwidth:
(define-param fcen 0.15) ; pulse center frequency
(define-param df 0.1) ; pulse width (in frequency)
(set! sources (list
(make source
(src (make gaussian-src (frequency fcen) (fwidth df)))
(component Ez) (center (+ r 0.1) 0))))
Finally, we are ready to run the simulation. The basic idea is to run until the sources are finished, and then to run for some additional period of time. In that additional period, we'll perform some signal-processing on the fields at some point with harminv to identify the frequencies and decay rates of the modes that were excited:
(run-sources+ 200
(at-beginning output-epsilon)
(after-sources (harminv Ez (vector3 (+ r 0.1)) fcen df)))
The signal-processing is performed by the harminv function, which takes four arguments: the field component (here Ez) and position (here (r + 0.1,0)) to analyze, and a frequency range given by a center frequency and bandwidth (here, the same as the source pulse). Note that we wrap harminv in (after-sources ...), since we only want to analyze the frequencies in the source-free system (the presence of a source will distort the analysis). At the end of the run, harminv prints a series of lines (beginning with harminv0:, to make it easy to grep for) listing the frequencies it found:
harminv0:, frequency, imag. freq., Q, |amp|, amplitude, error harminv0:, 0.117847040718825, -7.62561981749497e-4, 77.2704668861517, 0.0032044952042482, -0.00168219662723962+0.00272745376154268i, 1.04191977415041e-5 harminv0:, 0.146872136412678, -2.09246888543799e-4, 350.954170537011, 0.0248597274432886, 0.0221565453085791-0.0112735774509902i, 9.99544681424909e-6 harminv0:, 0.175013822666165, -5.36762125922926e-5, 1630.27358129302, 0.00594669979032255, -0.0058976965710993-7.61848772044579e-4i, 7.92698941172915e-7
There are six columns (in addition to the label), comma-delimited for easy import into other programs. The meaning of these columns is as follows. Harminv analyzes the fields f(t) at the given point, and expresses this as a sum of modes (in the specified bandwidth):
for complex amplitudes an and complex frequencies ωn. The six columns relate to these quantities. The first column is the real part of ωn, expressed in our usual 2πc units, and the second column is the imaginary part—a negative imaginary part corresponds to an exponential decay. This decay rate, for a cavity, is more often expressed as a dimensionless "lifetime" Q, defined by:
(Q is the number of optical periods for the energy to decay by exp( − 2π), and 1 / Q is the fractional bandwidth at half-maximum of the resonance peak in Fourier domain.) This Q is the third column of the output. The fourth and fifth columns are the absolute value | an | and complex amplitudes an. The last column is a crude measure of the error in the frequency (both real and imaginary)...if the error is much larger than the imaginary part, for example, then you can't trust the Q to be accurate. Note: this error is only the uncertainty in the signal processing, and tells you nothing about the errors from finite resolution, finite cell size, and so on!
An interesting question is how long should we run the simulation, after the sources are turned off, in order to analyze the frequencies. With traditional Fourier analysis, the time would be proportional to the frequency resolution required, but with harminv the time is much shorter. Here, for example, there are three modes. The last has a Q of 1630, which means that the mode decays for about 2000 periods or about 2000/0.175 = 104 time units. We have only analyzed it for about 200 time units, however, and the estimated uncertainty in the frequency is 10 − 6 (with an actual error of about 10 − 5, from below)! In general, you need to increase the run time to get more accuracy, and to find very high Q values, but not by much—in our own work, we have successfully found Q = 109 modes by analyzing only 200 periods.
In this case, we found three modes in the specified bandwith, at frequencies of 0.118, 0.147, and 0.175, with corresponding Q values of 77, 351, and 1630. Now, suppose that we want to actually see the field patterns of these modes. No problem: we just re-run the simulation with a narrow-band source around each mode and output the field at the end.
In particular, to output the field at the end we might add an (at-end output-efield-z) argument to our run-sources+ function, but this is problematic: we might be unlucky and output at a time when the Ez field is almost zero (i.e. when all of the energy is in the magnetic field), in which case the picture will be deceptive. Instead, at the end of the run we'll output 20 field snapshots over a whole period with the command:
(run-until (/ 1 fcen) (at-every (/ 1 fcen 20) output-efield-z))
Now, we can get our modes just by running e.g.:
unix% meep fcen=0.118 df=0.01 tut-ring.ctl
After each one of these commands, we'll convert the fields into PNG images and thence into an animated GIF (as with the bend movie, above), via:
unix% h5topng -RZc dkbluered -C tut-ring-eps-000000.00.h5 tut-ring-ez-*.h5 unix% convert tut-ring-ez-*.png tut-ring-ez-0.118.gif
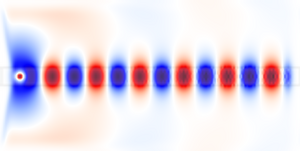
The resulting animations for (from left to right) 0.118, 0.147, and 0.175, are below, in which you can clearly see the radiating fields that produce the losses:
(Each of these modes is, of course, doubly-degenerate according to the representations of the 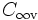 symmetry group. The other mode is simply a slight rotation of this mode to make it odd through the x axis, whereas we excited only the even modes due to our source symmetry.)
symmetry group. The other mode is simply a slight rotation of this mode to make it odd through the x axis, whereas we excited only the even modes due to our source symmetry.)
You may have noticed, by the way, that when you run with the narrow-bandwidth source, harminv gives you slightly different frequency and Q estimates, with a much smaller error estimate—this is not too strange, since by exciting a single mode you generate a cleaner signal that can be analyzed more accurately. For example, the narrow-bandwidth source for the ω = 0.175 mode gives:
harminv0:, 0.175021415872768, -5.5949172409816e-5, 1564.11085574932, 0.174688932289325, 0.0123277726314261+0.174253404805566i, 8.77730156016634e-11
which differs by about 0.00001 (10 − 5) from the earlier estimate; the difference in Q is, of course, larger because a small absolute error in ω gives a larger relative error in the small imaginary frequency.
See also: Ring resonator in cylindrical coordinates for how to solve this cylindrical geometry much more efficiently.
More examples
emacs and ctl
It is useful to have emacs use its scheme-mode for editing ctl files, so that hitting tab indents nicely, and so on. emacs does this automatically for files ending with ".scm"; to do it for files ending with ".ctl" as well, add the following lines to your ~/.emacs file:
(push '("\\.ctl\\'" . scheme-mode) auto-mode-alist)
or if your emacs version is 24.3 or earlier and you have other ".ctl" files which are not Scheme:
(if (assoc "\\.ctl" auto-mode-alist)
nil
(add-to-list 'auto-mode-alist '("\\.ctl\\'" . scheme-mode))))
(Incidentally, emacs scripts are written in "elisp," a language closely related to Scheme.)
If you don't use emacs (or derivatives such as Aquamacs), it would be good to find another editor that supports a Scheme mode. For example, jEdit is a free/open-source cross-platform editor with Scheme-syntax support. Another option is GNU gedit (for GNU/Linux and Unix); in fact, S. Hessam Moosavi Mehr has donated a hilighting mode for Meep/MPB that specially highlights the Meep/MPB keywords.