Meep Reference
From AbInitio
| Revision as of 08:05, 7 November 2005 (edit) Stevenj (Talk | contribs) (→source) ← Previous diff |
Revision as of 08:05, 7 November 2005 (edit) Stevenj (Talk | contribs) (→flux-region) Next diff → |
||
| Line 294: | Line 294: | ||
| ::The direction in which to compute the flux (e.g. <code>X</code>, <code>Y</code>, etcetera). The default is <code>AUTOMATIC</code>, in which the direction is determined by taking the normal direction if the flux region is a plane (or a line, in 2d). If the normal direction is ambiguous (e.g. for a point or volume), then you ''must'' specify the <code>direction</code> explicitly (not doing so will lead to an error). | ::The direction in which to compute the flux (e.g. <code>X</code>, <code>Y</code>, etcetera). The default is <code>AUTOMATIC</code>, in which the direction is determined by taking the normal direction if the flux region is a plane (or a line, in 2d). If the normal direction is ambiguous (e.g. for a point or volume), then you ''must'' specify the <code>direction</code> explicitly (not doing so will lead to an error). | ||
| :;<code>weight</code> [<code>cnumber</code>] | :;<code>weight</code> [<code>cnumber</code>] | ||
| - | ::A weight factor to multiply the flux by when it is computed. | + | ::A weight factor to multiply the flux by when it is computed; default is <code>1.0</code>. |
| Note that the flux is always computed in the ''positive'' coordinate direction, although this can effectively be flipped by using a <code>weight</code> of <code>-1.0</code>. (This is useful, for example, if you want to compute the outward flux through a box, so that the sides of the box add instead of subtract!) | Note that the flux is always computed in the ''positive'' coordinate direction, although this can effectively be flipped by using a <code>weight</code> of <code>-1.0</code>. (This is useful, for example, if you want to compute the outward flux through a box, so that the sides of the box add instead of subtract!) | ||
Revision as of 08:05, 7 November 2005
| Meep |
| Download |
| Release notes |
| FAQ |
| Meep manual |
| Introduction |
| Installation |
| Tutorial |
| Reference |
| C++ Tutorial |
| C++ Reference |
| Acknowledgements |
| License and Copyright |
Here, we document the features exposed to the user by the Meep package. We do not document the Scheme language or the functions provided by libctl (see also the libctl User Reference section of the libctl manual).
This page is simply a compact listing of the functions exposed by the interface; for a gentler introduction, see the Meep tutorial. Also, we note that this page is not, and probably never will be, a complete listing of all functions. In particular, because of the SWIG wrappers, every function in the C++ interface is accessible from Scheme, but not all of these functions are documented or intended for end users.
Contents |
Input Variables
These are global variables that you can set to control various parameters of the Meep computation. In brackets after each variable is the type of value that it should hold. (The classes, complex datatypes like geometric-object, are described in a later subsection. The basic datatypes, like integer, boolean, cnumber, and vector3, are defined by libctl.)
-
geometry[list ofgeometric-objectclass] - Specifies the geometric objects making up the structure being simulated. When objects overlap, later objects in the list take precedence. Defaults to no objects (empty list).
-
sources[list ofsourceclass] - Specifies the current sources to be present in the simulation; defaults to none.
-
symmetries[list ofsymmetryclass] - Specifies the spatial (mirror/rotation) symmetries to exploit in the simulation (defaults to none). The symmetries must be obeyed by both the structure and by the sources. See also: Exploiting symmetry in Meep.
-
pml-layers[list ofpmlclass] - Specifies the absorbing PML boundary layers to use; defaults to none.
-
default-material[material-typeclass] - Holds the default material that is used for points not in any object of the geometry list. Defaults to
air(ε of 1). -
geometry-lattice[latticeclass] - Specifies the the size of the unit cell (which is centered on the origin of the coordinate system). If any dimension of the lattice
sizeis the special valueno-size, then the dimension of the lattice is reduced (i.e. it becomes two- or one-dimensional) by default. Defaults to a cubic cell of unit size. -
dimensions[integer] - Explicitly specifies the dimensionality of the simulation, if the value is less than 3. If the value is 3 (the default), then the dimensions are automatically reduced if possible when any of the
geometry-latticesizes areno-size. Ifdimensionsis the special value ofCYLINDRICAL, then cylindrical coordinates are used and the x and z dimensions are interpreted as r and z, respectively. -
m[number] - For
CYLINDRICALsimulations, specifies that the angular φ dependence of the fields is of the form eimφ (default ism=0). If the simulation cell includes the origin r = 0, thenmmust be an integer. -
resolution[numberorvector3] - Specifies the computational grid resolution, in pixels per distance unit. Defaults to
10. -
k-point[falseorvector3] - If
false(the default), then the boundaries are perfect metallic (zero electric field). If a vector, then the boundaries are Bloch-periodic: the fields at one side are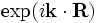 times the fields at the other side, separated by the lattice vector
times the fields at the other side, separated by the lattice vector 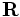 . The
. The k-pointvector is specified in Cartesian coordinates, in units of 2π/distance. (This is different from MPB, equivalent to taking MPB'sk-pointsthrough the functionreciprocal->cartesian.) -
ensure-periodicity[boolean] - If
true(the default), and if the boundary conditions are periodic (k-pointis notfalse), then the geometric objects are automatically repeated periodically according to the lattice vectors (the size of the computational cell). -
force-complex-fields?[boolean] - By default, Meep runs its simulations with purely real fields whenever possible. It uses complex fields (which require twice the memory and computation) if the
k-pointis non-zero or ifmis non-zero. However, by settingforce-complex-fields?totrue, Meep will always use complex fields. See also: Complex fields in Meep. -
filename-prefix[string] - A string prepended to all output filenames. Defaults to the name of the current ctl file, with ".ctl" replaced by "-" (e.g.
foo.ctluses a"foo-"prefix). -
Courant[number] - Specify the Courant factor S which relates the time step size to the spatial discretization: cΔt = SΔx. Default is
0.5. For numerical stability, the Courant factor must be at most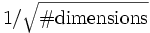 , and in practice should be slightly smaller.
, and in practice should be slightly smaller.
-
output-volume[meep::geometric_volume*] - Specifies the default region of space that is output by the HDF5 output functions (below); see also the
(volume ...)function to createmeep::geometric_volume*objects. The default is'()(null), which means that the whole computational cell is output. Normally, you should use the(in-volume ...)function to modify the output volume instead of settingoutput-volumedirectly. -
progress-interval[number] - Time interval (seconds) after which Meep prints a progress message; default is 4 seconds.
The require a bit more understanding of the inner workings of Meep to use (see also the SWIG wrappers).
-
structure[meep::structure*] - Pointer to the current structure being simulated; initialized by
(init-structure)which is called automatically by(init-fields)which is called automatically by any of the(run)functions. -
fields[meep::fields*] - Pointer to the current fields being simulated; initialized by
(init-fields)which is called automatically by any of the(run)functions. -
num-chunks[integer] - Minimum number of "chunks" (subarrays) to divide the structure/fields into (default 0); actual number is determined by number of processors, PML layers, etcetera. (Mainly useful for debugging.)
Predefined Variables
Variables predefined for your convenience and amusement.
-
air,vacuum[material-typeclass] - Two aliases for a predefined material type with a dielectric constant of 1.
-
metal[material-typeclass] - A predefined material type corresponding to a perfectly conducting metal (in which the electric field is zero).
-
nothing[material-typeclass] - A material that, effectively, punches a hole through other objects to the background (
default-materialorepsilon-input-file). -
infinity[number] - A big number (1.0e20) to use for "infinite" dimensions of objects.
-
pi[number] - π (3.14159...).
Constants (enumerated types)
Several of the functions/classes in Meep ask you to specify e.g. a field component or a direction in the grid. These should be one of the following constants:
-
directionconstants - Specify a direction in the grid. One of
X,Y,Z,R,Pfor: x, y, z, r, φ, respectively. -
boundary-sideconstants - Specify particular boundary in some direction (e.g. + x or − x). One of
LoworHigh. -
componentconstants - Specify a particular field (or other) component. One of
Ex,Ey,Ez,Er,Ep,Hx,Hy,Hz,Hy,Hp,Hz,Dx,Dy,Dz,Dr,Dp,Dielectric, for: Ex, Ey, Ez, Er, Eφ, Hx, Hy, Hz, Hr, Hφ, Dx, Dy, Dz, Dr, Dφ,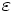 , respectively.
, respectively.
-
derived-componentconstants - These are additional components, which are not actually stored by Meep but are computed as needed, mainly for use in output functions. One of
Sx,Sy,Sz,Sr,Sp,EnergyDensity,D-EnergyDensity,H-EnergyDensityfor: Sx, Sy, Sz, Sr, Sφ (components of the Poynting vector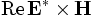 ),
), 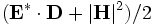 ,
, 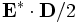 ,
, 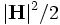 , respectively.
, respectively.
Classes
Classes are complex datatypes with various "properties" which may have default values. Classes can be "subclasses" of other classes; subclasses inherit all the properties of their superclass, and can be used any place the superclass is expected. An object of a class is constructed with:
(make class (prop1 val1) (prop2 val2) ...)
See also the libctl manual.
Meep defines several types of classes, the most numerous of which are the various geometric object classes (which are the same as those used in MPB. You can also get a list of the available classes, along with their property types and default values, at runtime with the (help) command.
lattice
The lattice class is normally used only for the geometry-lattice variable, which sets the size of the computational cell. In MPB, you can use this to specify a variety of affine lattice structures. In Meep, only rectangular Cartesian computational cells are supported, so the only property of lattice that you should normally use is its size.
-
lattice - Properties:
-
size[vector3] - The size of the computational cell. Defaults to unit lengths.
If any dimension has the special size no-size, then the dimensionality of the problem is (essentially) reduced by one; strictly speaking, the dielectric function is taken to be uniform along that dimension.
Because Maxwell's equations are scale-invariant, you can use any units of distance you want to specify the cell size: nanometers, inches, parsecs, whatever. However, it is usually convenient to pick some characteristic lengthscale of your problem and set that length to 1. See also Meep Introduction#Units in Meep.
material-type
This class is used to specify the materials that geometric objects are made of. Currently, there are three subclasses, dielectric, perfect-metal, and material-function.
-
dielectric - A uniform, isotropic, possibly nonlinear or dispersive, dielectric material; see also Dielectric materials in Meep. It has three properties:
-
epsilon[number] - The dielectric constant (must be positive). No default value. You can also use
(index n)as a synonym for(epsilon (* n n)). -
chi2[number] - The Kerr susceptibility
\chi^{(2)}. - polarizations [list of
polarizabilityclass] - List of dispersive polarizabilities (see below) added to the dielectric constant, in order to model material dispersion; defaults to none.
-
-
perfect-metal - A perfectly conducting metal; this class has no properties and you normally just use the predefined
metalobject, above. (To model imperfect conductors, use a dispersive dielectric material.) -
material-function - This material type allows you to specify the material as an arbitrary function of position. It has one property:
-
material-func[function] - A function of one argument, the position
vector3, that returns the material at that point. Note that the function you supply can return any material; wild and crazy users could even return anothermaterial-functionobject (which would then have its function invoked in turn).
-
Dispersive dielectric materials, above, are specified via a list of objects of type polarizability, which is another class with four properties:
-
polarizability - Specifies a single dispersive polarizability of damped harmonic form (see Material dispersion), with the parameters:
-
omega[number] - The resonance frequency ωn.
-
gamma[number] - The resonance frequency γn.
-
sigma[number] - The scale factor σn.
-
energy-saturation[number] - See Saturable gain in Meep.
-
geometric-object
This class, and its descendants, are used to specify the solid geometric objects that form the dielectric structure being simulated. The base class is:
-
geometric-object - Properties:
-
material[material-typeclass] - The material that the object is made of (usually some sort of dielectric). No default value (must be specified).
-
center[vector3] - Center point of the object. No default value.
-
One normally does not create objects of type geometric-object directly, however; instead, you use one of the following subclasses. Recall that subclasses inherit the properties of their superclass, so these subclasses automatically have the material and center properties (which must be specified, since they have no default values).
In a two-dimensional calculation, only the intersections of the objects with the x-y plane are considered.
-
sphere - A sphere. Properties:
-
radius[number] - Radius of the sphere. No default value.
-
-
cylinder - A cylinder, with circular cross-section and finite height. Properties:
-
radius[number] - Radius of the cylinder's cross-section. No default value.
-
height[number] - Length of the cylinder along its axis. No default value.
-
axis[vector3] - Direction of the cylinder's axis; the length of this vector is ignored. Defaults to point parallel to the z axis.
-
-
cone - A cone, or possibly a truncated cone. This is actually a subclass of
cylinder, and inherits all of the same properties, with one additional property. The radius of the base of the cone is given by theradiusproperty inherited fromcylinder, while the radius of the tip is given by the new property:-
radius2[number] - Radius of the tip of the cone (i.e. the end of the cone pointed to by the
axisvector). Defaults to zero (a "sharp" cone).
-
-
block - A parallelepiped (i.e., a brick, possibly with non-orthogonal axes). Properties:
-
size[vector3] - The lengths of the block edges along each of its three axes. Not really a 3-vector, but it has three components, each of which should be nonzero. No default value.
-
e1,e2,e3[vector3] - The directions of the axes of the block; the lengths of these vectors are ignored. Must be linearly independent. They default to the three lattice directions.
-
-
ellipsoid - An ellipsoid. This is actually a subclass of
block, and inherits all the same properties, but defines an ellipsoid inscribed inside the block.
Here are some examples of geometric objects created using the above classes, assuming mat is some material we have defined:
; A cylinder of infinite radius and height 0.25 pointing along the x axis,
; centered at the origin:
(make cylinder (center 0 0 0) (material mat)
(radius infinity) (height 0.25) (axis 1 0 0))
; An ellipsoid with its long axis pointing along (1,1,1), centered on
; the origin (the other two axes are orthogonal and have equal
; semi-axis lengths):
(make ellipsoid (center 0 0 0) (material mat)
(size 0.8 0.2 0.2)
(e1 1 1 1)
(e2 0 1 -1)
(e3 -2 1 1))
; A unit cube of material m with a spherical air hole of radius 0.2 at
; its center, the whole thing centered at (1,2,3):
(set! geometry (list
(make block (center 1 2 3) (material mat) (size 1 1 1))
(make sphere (center 1 2 3) (material air) (radius 0.2))))
symmetry
This class is used for the symmetries input variable, to specify symmetries (which must preserve both the structure and the sources) for Meep to exploit. Any number of symmetries can be exploited simultaneously, but there is no point in specifying redundant symmetries: the computational cell can be reduced by at most a factor of 4 in 2d and 8 in 3d. See also Exploiting symmetry in Meep.
-
symmetry - A single symmetry to exploit. This is the base class of the specific symmetries below, so normally you don't create it directly. However, it has two properties which are shared by all symmetries:
-
direction[directionconstant] - The direction of the symmetry (the normal to a mirror plane or the axis for a rotational symmetry). e.g.
X,Y, ... (only Cartesian/grid directions are allowed). No default value. -
phase[cnumber] - An additional phase to multiply the fields by when operating the symmetry on them; defaults to
1.0. e.g. a phase of-1for a mirror plane corresponds to an odd mirror. (Technically, you are essentially specifying the representation of the symmetry group that your fields and sources transform under.)
-
The specific symmetry sub-classes are:
-
mirror-sym - A mirror symmetry plane. Here, the
directionis the direction normal to the mirror plane. -
rotate2-sym - A 180° (twofold) rotational symmetry (a.k.a. C2). Here, the
directionis the axis of the rotation. -
rotate2-sym - A 90° (fourfold) rotational symmetry (a.k.a. C4). Here, the
directionis the axis of the rotation.
pml
This class is used for specifying the PML absorbing boundary layers around the cell, if any, via the pml-layers input variable. See also Perfectly matched layers. pml-layers can be zero or more pml objects, with multiple objects allowing you to specify different PML layers on different boundaries.
-
pml - A single PML layer specification, which sets up one or more PML layers around the boundaries according to the following four properties.
-
thickness[number] - The spatial thickness of the PML layer (which extends from the boundary towards the inside of the computational cell). The thinner it is, the more numerical reflections become a problem. No default value.
-
direction[directionconstant] - Specify the direction of the boundaries to put the PML layers next to. e.g. if
X, then specifies PML on the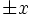 boundaries (depending on the value of
boundaries (depending on the value of side, below). Default is the special valueALL, which puts PML layers on the boundaries in all directions. -
side[boundary-sideconstant] - Specify which side,
LoworHighof the boundary or boundaries to put PML on. e.g. if side isLowand direction isX, then a PML layer is added to the − x boundary. Default is the special valueALL, which puts PML layers on both sides. -
strength[number] - A strength (default is
1.0) to multiply the PML absorption coefficient by. A strength of2.0will square the theoretical reflection coefficient of the PML (making it smaller), but will also increase numerical reflections.
-
source
The source class is used to specify the current sources (via the sources input variable). Note that all sources in Meep are separable in time and space, i.e. of the form \mathbf{J}(\mathbf{x},t) = \mathbf{A}(\mathbf{x}) \cdot f(t) for some functions 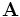 and f. (Non-separable sources can be simulated, however, by modifying the sources after each time step.) When real fields are being used (which is the default in many cases...see the
and f. (Non-separable sources can be simulated, however, by modifying the sources after each time step.) When real fields are being used (which is the default in many cases...see the force-complex-fields? input variable), only the real part of the current source is used by Meep.
-
source - The source class has the following properties:
-
src[src-timeclass] - Specify the time-dependence of the source (see below). No default.
-
component[componentconstant] - Specify the direction and type of the current component: e.g.
Ex,Ey, etcetera for an electric current, andHx,Hy, etcetera for a magnetic current. Note that currents pointing in an arbitrary direction are specified simply as multiple current sources with the appropriate amplitudes for each component. No default. center[vector3]- The location of the center of the current source in the computational cell; no default.
size[vector3]- The size of the current distribution along each direction of the computational cell. The default is (0,0,0): a point source.
amplitude[cnumber]- An overall (complex) amplitude multiplying the the current source. Default is
1.0. amp-func[function]- A Scheme function of a single argument, that takes a vector3 giving a position and returns a (complex) current amplitude for that point. The position argument is relative to the
centerof the current source, so that you can move your current around without changing your function. The default is'()(null), meaning that a constant amplitude of 1.0 is used. Note that your amplitude function (if any) is multiplied by theamplitudeproperty, so both properties can be used simultaneously.
-
The src-time object, which specifies the time dependence of the source, can be one of the following three classes.
-
continuous-src - A continuous-wave source proportional to exp( − iωt), possibly with a smooth (exponential/tanh) turn-on/turn-off. It has the properties:
frequency[number]- The frequency ω, in units of 2πc (see Units in Meep). No default value. You can instead specify
(wavelength x)or(period x), which are both a synonym for(frequency (/ 1 x)); i.e. 1/ω in these units is the vacuum wavelength or the temporal period. start-time[number]- The starting time for the source; default is
0(turn on at t = 0). end-time[number]- The end time for the source; default is
infinity(never turn off). width[number]- Roughly, the temporal width of the smoothing (technically, the inverse of the exponential rate at which the current turns off and on). Default is
0(no smoothing). You can instead specify(fwidth x), which is a synonym for(width (/ 1 x))(i.e. the frequency width is proportional to the inverse of the temporal width). cutoff[number]- How many
widths the current decays for before we cut it off and set it to zero; the default is3.0. A larger value ofcutoffwill reduce the amount of high-frequency components that are introduced by the start/stop of the source, but will of course lead to longer simulation times.
-
gaussian-src - A Gaussian-pulse source roughly proportional to exp( − iωt − (t − t0)2 / 2w2), It has the properties:
- The center frequency ω, in units of 2πc (see Units in Meep). No default value. You can instead specify
(wavelength x)or(period x), which are both a synonym for(frequency (/ 1 x)); i.e. 1/ω in these units is the vacuum wavelength or the temporal period. width[number]- The width w used in the Gaussian. No default value. You can instead specify
(fwidth x), which is a synonym for(width (/ 1 x))(i.e. the frequency width is proportional to the inverse of the temporal width). start-time[number]- The starting time for the source; default is
0(turn on at t = 0). cutoff[number]- How many
widths the current decays for before we cut it off and set it to zero—this applies for both turn-on and turn-off of the pulse. The default is5.0. A larger value ofcutoffwill reduce the amount of high-frequency components that are introduced by the start/stop of the source, but will of course lead to longer simulation times.
- The center frequency ω, in units of 2πc (see Units in Meep). No default value. You can instead specify
-
custom-src - A user-specified source function f(t). You can also specify start/end times (at which point your current is set to zero whether or not your function is actually zero). These are optional, but you must specify an
end-timeexplicitly if you want functions likerun-sourcesto work, since they need to know when your source turns off.-
src-func[function] - The function f(t) specifying the time-dependence of the source. It should take one argument (the time in Meep units) and return a complex number.
start-time[number]- The starting time for the source; default is
(- infinity)(turn on at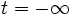 ). Note, however, that the simulation normally starts at t = 0 with zero fields as the initial condition, so there is implicitly a sharp turn-on at t = 0 whether you specify it or not.
). Note, however, that the simulation normally starts at t = 0 with zero fields as the initial condition, so there is implicitly a sharp turn-on at t = 0 whether you specify it or not.
end-time[number]- The end time for the source; default is
infinity(never turn off).
-
flux-region
A flux-region object is used with add-flux below to specify a region in which Meep should accumulate the appropriate Fourier-transformed fields in order to compute a flux spectrum.
flux-region- A region (volume, plane, line, or point) in which to compute the integral of the Poynting vector of the Fourier-transformed fields. Its properties are:
center[vector3]- The center of the flux region (no default).
size[vector3]- The size of the flux region along each of the coordinate axes; default is (0,0,0) (a single point).
direction[directionconstant]- The direction in which to compute the flux (e.g.
X,Y, etcetera). The default isAUTOMATIC, in which the direction is determined by taking the normal direction if the flux region is a plane (or a line, in 2d). If the normal direction is ambiguous (e.g. for a point or volume), then you must specify thedirectionexplicitly (not doing so will lead to an error). weight[cnumber]- A weight factor to multiply the flux by when it is computed; default is
1.0.
Note that the flux is always computed in the positive coordinate direction, although this can effectively be flipped by using a weight of -1.0. (This is useful, for example, if you want to compute the outward flux through a box, so that the sides of the box add instead of subtract!)
Miscellaneous functions
Here, we describe a number of miscellaneous useful functions provided by Meep.
See also the reference section of the libctl manual, which describes a number of useful functions defined by libctl.
Geometry utilities
Some utility functions are provided to help you manipulate geometric objects:
-
(shift-geometric-object obj shift-vector) - Translate
objby the 3-vectorshift-vector. -
(geometric-object-duplicates shift-vector min-multiple max-multiple obj) - Return a list of duplicates of
obj, shifted by various multiples ofshift-vector(frommin-multipletomax-multiple, inclusive, in steps of 1). -
(geometric-objects-duplicates shift-vector min-multiple max-multiple obj-list) - Same as
geometric-object-duplicates, except operates on a list of objects,obj-list. If A appears before B in the input list, then all the duplicates of A appear before all the duplicates of B in the output list. -
(geometric-objects-lattice-duplicates obj-list [ ux uy uz ]) - Duplicates the objects in
obj-listby multiples of the Cartesian basis vectors, making all possible shifts of the "primitive cell" (see below) that fit inside the lattice cell. (This is useful for supercell calculations; see the [user-tutorial.html tutorial].) The primitive cell to duplicate isuxbyuybyuz, in units of the Cartesian basis vectors. These three parameters are optional; any that you do not specify are assumed to be1. -
(point-in-object? point obj) - Returns whether or not the given 3-vector
pointis inside the geometric objectobj. -
(point-in-periodic-object? point obj) - As
point-in-object?, but also checks translations of the given object by the lattice vectors. -
(display-geometric-object-info indent-by obj) - Outputs some information about the given
obj, indented byindent-byspaces.
Field computations
Meep supports a large number of functions to perform computations on the fields. Currently, most of them are accessed via the lower-level C++/SWIG interface, but we are slowly adding simpler, higher-level versions of them here.
(get-field-point c pt)- Given a
componentorderived-componentconstantcand avector3pt, returns the value of that component at that point. (get-epsilon-point pt)- Equivalent to
(get-field-point Dielectric pt).
(More to come...)
Reloading parameters
Once the fields have been initialized, you can change the values of various parameters by using the following functions:
(reset-meep)- Reset all of Meep's parameters, deleting the fields, structures, etcetera, from memory as if you had not run any computations.
(restart-fields)- Restart the fields at time zero, with zero fields. (Does not reset the Fourier transforms of the flux planes, which continue to be accumulated.)
(change-k-point! k)- Change the
k-point(the Bloch periodicity).
(More to come...)
Flux spectra
Given a bunch of flux-region objects (see above), you can tell Meep to accumulate the Fourier transforms of the fields in those regions in order to compute flux spectra. See also the transmission/reflection spectra introduction and the Meep tutorial. The most important function is:
(add-flux fcen df nfreq flux-regions...)- Add a bunch of
flux-regions to the current simulation (initializing the fields if they have not yet been initialized), telling Meep to accumulate the appropriate field Fourier transforms fornfreqequally spaced frequencies covering the frequency rangefcen-df/2tofcen+df/2. Return a flux object, which you can pass to the functions below to get the flux spectrum, etcetera.
As described in the tutorial, you normally use add-flux via statements like:
(define transmission (add-flux ...))
to store the flux object in a variable. add-flux initializes the fields if necessary, just like calling run, so you should only call it after setting up your geometry, sources, pml-layers, etcetera. You can create as many flux objects as you want, e.g. to look at powers flowing in different regions or in different frequency ranges. Note, however, that Meep has to store (and update at every time step) a number of Fourier components equal to the number of grid points intersecting the flux region multiplied by the number of electric and magnetic field components required to get the Poynting vector multiplied by nfreq, so this can get quite expensive (in both memory and time) if you want a lot of frequency points over large regions of space.
Once you have called add-flux, the Fourier transforms of the fields are accumulated automatically during time-stepping by the run functions. At any time, you can ask for Meep to print out the current flux spectrum via:
(display-fluxes fluxes...)- Given a number of flux objects, this displays a comma-separated table of frequencies and flux spectra, prefixed by "flux1:" or similar (where the number is incremented after each run). All of the fluxes should be for the same
fcen/df/nfreq. The first column are the frequencies, and subsequent columns are the flux spectra.
You might have to do something lower-level if you have multiple flux regions corresponding to different frequency ranges, or have other special needs. (display-fluxes f1 f2 f3) is actually equivalent to (display-csv "flux" (get-flux-freqs f1) (get-fluxes f1) (get-fluxes f2) (get-fluxes f3), where display-csv takes a bunch of lists of numbers and prints them as a comma-separated table, and we are calling two lower-level functions:
(get-flux-freqs flux)- Given a flux object, returns a list of the frequencies that it is computing the spectrum for.
(get-fluxes flux)- Given a flux object, returns a list of the current flux spectrum that it has accumulated.
As described in the Meep tutorial, for a reflection spectrum you often want to save the Fourier-transformed fields from a "normalization" run and then load them into another run to be subtracted. This can be done via:
(save-flux filename flux)- Save the Fourier-transformed fields corresponding to the given flux object in an HDF5 file of the given name (without the ".h5" suffix) (the current filename-prefix is prepended automatically).
(load-flux filename flux)- Load the Fourier-transformed fields into the given flux object (replacing any values currently there) from an HDF5 file of the given name (without the ".h5" suffix) (the current filename-prefix is prepended automatically). You must load from a file that was saved by
save-fluxin a simulation of the same dimensions (for both the computational cell and the flux regions) with the same number of processors. (load-minus-flux filename flux)- As
load-flux, but negates the Fourier-transformed fields after they are loaded. This means that they will be subtracted from any future field Fourier transforms that are accumulated. (scale-flux-fields s flux)- Scale the Fourier-transformed fields in
fluxby the complex numbers. e.g.load-minus-fluxis equivalent toload-fluxfollowed byscale-flux-fieldswiths=-1.

