Meep FAQ
From AbInitio
| Revision as of 15:49, 16 May 2009 (edit) Stevenj (Talk | contribs) (→How do I set the imaginary part of ε?) ← Previous diff |
Revision as of 15:57, 16 May 2009 (edit) Stevenj (Talk | contribs) (→Physics - negative-epsilon FAQ) Next diff → |
||
| Line 27: | Line 27: | ||
| Meep doesn't implement a frequency-independent complex ε. Not only is this not physical, but it also leads to both exponentially decaying and exponentially growing solutions in Maxwell's equations from positive- and negative-frequency Fourier components, respectively, so it cannot be simulated in the time domain. | Meep doesn't implement a frequency-independent complex ε. Not only is this not physical, but it also leads to both exponentially decaying and exponentially growing solutions in Maxwell's equations from positive- and negative-frequency Fourier components, respectively, so it cannot be simulated in the time domain. | ||
| + | |||
| + | ===Why does my simulation diverge if ε < 0?=== | ||
| + | |||
| + | Maxwell's equations are unstable for a frequency-independent negative ε. For any physical medium with negative ε, there must be dispersion, and you must likewise use dispersive materials in Meep to have negative ε at some desired frequency. (The requirement of dispersion to obtain negative ε follows from the Kramers–Kronig relations, and also follows from thermodynamic considerations that the energy in the electric field must be positive; see, for example, ''Electrodynamics of Continuous Media'' by Landau, Pitaevskii, and Lifshitz.) | ||
| + | |||
| + | If you solve Maxwell's equations in a homogenous-epsilon material at some real wavevector '''k''', you get a dispersion relation <math>\omega^2 = c^2 |\mathbf{k}|^2 / \varepsilon</math>. If ε is positive, there are two real solutions <math>\omega^2 = \pm c |\mathbf{k}| / \sqrt{\varepsilon}</math>, giving oscillating solutions. If ε is negative, there are two ''imaginary'' solutions ω, corresponding to exponentially decaying and ''exponentially growing solutions'' from any current source (which can always be spatially decomposed into a superposition of real-'''k''' values via a spatial Fourier transform). | ||
| + | |||
| + | If you do a simulation of any kind in the time domain (not just FDTD), you pretty much can't avoid exciting both the decaying and the growing solutions. | ||
| + | |||
| + | See [[Materials in Meep]] for how to include dispersive materials (which can have negative ε and loss) in Meep. | ||
| ==Usage== | ==Usage== | ||
| [[Category:Meep]] | [[Category:Meep]] | ||
Revision as of 15:57, 16 May 2009
| Meep |
| Download |
| Release notes |
| FAQ |
| Meep manual |
| Introduction |
| Installation |
| Tutorial |
| Reference |
| C++ Tutorial |
| C++ Reference |
| Acknowledgements |
| License and Copyright |
The following are frequently asked questions about Meep. Or, at any rate, they will be, now that Meep has been released.
Contents |
General
What is Meep?
Meep is our free software for finite-difference time-domain simulation. For the meaning of the name "Meep", see Meep acronym expansions.
Installation
Where can I install Meep?
Meep should run on any Unix-like system, from individual machines to clusters to large parallel supercomputers. We do most of our development on GNU/Linux systems, and precompiled packages are available for Debian and Ubuntu. It should also be possible to install Meep on Windows using the free Cygwin Unix-compatibility environment. Installing Meep from source code requires some understanding of Unix, however, especially to install the various prerequisites, and we recommend consulting a local Unix guru at your institution if you run into trouble.
Guile is installed, but configure complains that it can't find guile
With most GNU/Linux distributions (and Cygwin), packages like Guile are split into two pieces: a guile package that just contains the libraries and executables, and a guile-dev or guile-devel package that contains the header files and other things needed to compile programs using Guile. Usually, the former is installed by default, by the latter is not. You need to install both, which means that you probably need to install guile-dev. (Similarly for any other library packages needed by Meep.)
Physics
How does the current amplitude relate to the resulting field amplitude?
There is no simple formula relating the input current amplitude (J in Maxwell's equations) to the resulting fields (E) etcetera, even at the same point as the current. The exact same current will produce a different field (and radiate a different total power) depending upon the surrounding materials/geometry, and depending on the frequency. (This is a physical consequence of the geometry's effect on the local density of states; it can also be thought of as feedback from reflections on the source. As a simple example, if you put a current source inside a perfect electric conductor, the resulting field will be zero. As another example, the frequency-dependence of the radiated power in vacuum is part of the reason why the sky is blue.)
If you are worried about this, then you are probably setting up your calculation in the wrong way. Especially in linear materials, the absolute magnitude of the field is useless; the only meaningful quantities are dimensionless ratios like the fractional transmission (the transmitted power relative to the transmitted power in some reference calculation). Almost always, you want to perform two calculations, one of which is a reference, and compute the ratio of a result in one calculation to the result in the reference. For nonlinear calculations, see Units and nonlinearity in Meep.
How do I set the imaginary part of ε?
If you only care about the imaginary part of ε in a narrow bandwidth around some frequency ω, you should set it by using the electric conductivity as described in Conductivity in Meep. If you care about the imaginary part of ε over a broad bandwidth, then for any physical material the imaginary part will be frequency-dependent and you will have to fit it to Meep's dispersive-ε support (see Material dispersion in Meep).
Meep doesn't implement a frequency-independent complex ε. Not only is this not physical, but it also leads to both exponentially decaying and exponentially growing solutions in Maxwell's equations from positive- and negative-frequency Fourier components, respectively, so it cannot be simulated in the time domain.
Why does my simulation diverge if ε < 0?
Maxwell's equations are unstable for a frequency-independent negative ε. For any physical medium with negative ε, there must be dispersion, and you must likewise use dispersive materials in Meep to have negative ε at some desired frequency. (The requirement of dispersion to obtain negative ε follows from the Kramers–Kronig relations, and also follows from thermodynamic considerations that the energy in the electric field must be positive; see, for example, Electrodynamics of Continuous Media by Landau, Pitaevskii, and Lifshitz.)
If you solve Maxwell's equations in a homogenous-epsilon material at some real wavevector k, you get a dispersion relation 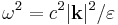 . If ε is positive, there are two real solutions
. If ε is positive, there are two real solutions 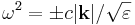 , giving oscillating solutions. If ε is negative, there are two imaginary solutions ω, corresponding to exponentially decaying and exponentially growing solutions from any current source (which can always be spatially decomposed into a superposition of real-k values via a spatial Fourier transform).
, giving oscillating solutions. If ε is negative, there are two imaginary solutions ω, corresponding to exponentially decaying and exponentially growing solutions from any current source (which can always be spatially decomposed into a superposition of real-k values via a spatial Fourier transform).
If you do a simulation of any kind in the time domain (not just FDTD), you pretty much can't avoid exciting both the decaying and the growing solutions.
See Materials in Meep for how to include dispersive materials (which can have negative ε and loss) in Meep.

