Faddeeva Package
From AbInitio
| Revision as of 03:45, 4 November 2012 (edit) Stevenj (Talk | contribs) (→Complex error functions) ← Previous diff |
Revision as of 03:47, 4 November 2012 (edit) Stevenj (Talk | contribs) Next diff → |
||
| Line 10: | Line 10: | ||
| Given the Faddeeva function ''w''(''z''), one can also easily compute [[w:Voigt profile|Voigt functions]] and similar related functions as well. In benchmarks of our code, we find that it is competitive or faster than most competing software for these functions, especially in the complex plane (but we also have special-case optimizations for purely real or imaginary arguments), and we find that the accuracy is typically near [[w:Machine epsilon|machine precision]]. | Given the Faddeeva function ''w''(''z''), one can also easily compute [[w:Voigt profile|Voigt functions]] and similar related functions as well. In benchmarks of our code, we find that it is competitive or faster than most competing software for these functions, especially in the complex plane (but we also have special-case optimizations for purely real or imaginary arguments), and we find that the accuracy is typically near [[w:Machine epsilon|machine precision]]. | ||
| - | Because all of the algorithms are based on algorithms for the Faddeeva function, we call this the '''Faddeeva package'''. | + | Because all of the algorithms are based on algorithms for the Faddeeva function, we call this the '''Faddeeva Package'''. |
| ==Download== | ==Download== | ||
Revision as of 03:47, 4 November 2012
Steven G. Johnson has written free/open-source C++ code (with wrappers for other languages) to compute the various error functions of arbitrary complex arguments. In particular, we provide:
- The Faddeeva function
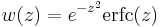 , where erfc is the complementary error function.
, where erfc is the complementary error function.
- The error function
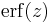
- The complementary error function
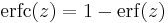
- The scaled complementary error function
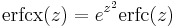
- The imaginary error function
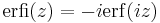
- The Dawson function
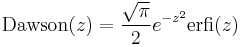
Given the Faddeeva function w(z), one can also easily compute Voigt functions and similar related functions as well. In benchmarks of our code, we find that it is competitive or faster than most competing software for these functions, especially in the complex plane (but we also have special-case optimizations for purely real or imaginary arguments), and we find that the accuracy is typically near machine precision.
Because all of the algorithms are based on algorithms for the Faddeeva function, we call this the Faddeeva Package.
Contents |
Download
Download the source code from:
- http://ab-initio.mit.edu/Faddeeva.cc and http://ab-initio.mit.edu/Faddeeva.hh (updated 3 November 2012)
See also below for wrappers to call the Faddeeva package from other languages.
Usage
To use the code, include the Faddeeva.hh header file:
#include "Faddeeva.hh"
and compile and link the Faddeeva.cc source code. You can then call various functions. For example:
extern std::complex<double> Faddeeva::w(std::complex<double> z, double relerr=0);
The function Faddeeva::w(z, relerr) computes w(z) to a desired relative error relerr.
Omitting the relerr argument, or passing relerr=0 (or any relerr less than machine precision ε≈10−16), corresponds to requesting machine precision, and in practice a relative error < 10−13 is usually achieved. Specifying a larger value of relerr may improve performance (at the expense of accuracy).
Similarly, the erf, erfc, erfcx, erfi, and Dawson functions are computed by calling:
extern std::complex<double> Faddeeva::erf(std::complex<double> z, double relerr=0); extern std::complex<double> Faddeeva::erfc(std::complex<double> z, double relerr=0); extern std::complex<double> Faddeeva::erfcx(std::complex<double> z, double relerr=0); extern std::complex<double> Faddeeva::erfi(std::complex<double> z, double relerr=0); extern std::complex<double> Faddeeva::Dawson(std::complex<double> z, double relerr=0);
Since these functions are purely real for real arguments z=x, we provide the following specialized interfaces for convenience (and a slight performance gain, although the complex functions above automatically execute specialized code for purely real arguments):
extern double Faddeeva::erf(double x); extern double Faddeeva::erfc(double x); extern double Faddeeva::erfcx(double x); extern double Faddeeva::erfi(double x); extern double Faddeeva::Dawson(double x);
(These functions always compute to maximum accuracy, usually near machine precision.)
It is also sometimes useful to compute Im[w(x)] for real x, since ![\mathrm{Im}[w(z)] = e^{-z^2} \mathrm{erfi}(z)](/wiki/images/math/9/6/5/965b83f3ee1d4c7fb9080cfdb2ca3493.png) . Note that Re[w(x)] is simply exp(−x2) for real x. Im[w(x)] can be computed efficiently by calling:
. Note that Re[w(x)] is simply exp(−x2) for real x. Im[w(x)] can be computed efficiently by calling:
extern double Faddeeva::w_im(double x);
(Again, this computes to nearly machine precision.)
Wrappers: Matlab, GNU Octave, and Python
Wrappers are available for this function in other languages.
- Matlab (also available here): A function
Faddeeva_w(z, relerr), where the arguments have the same meaning as above (therelerrargument is optional) can be downloaded from Faddeeva_w_mex.cc (along with the help file Faddeeva_w.m. Compile it into an octave plugin with:
mex -output Faddeeva_w -O Faddeeva_w_mex.cc Faddeeva_w.cc
- GNU Octave: A function
Faddeeva_w(z, relerr), where the arguments have the same meaning as above (therelerrargument is optional) can be downloaded from Faddeeva_w_oct.cc. Compile it into a MEX file with:
mkoctfile -DMPICH_SKIP_MPICXX=1 -DOMPI_SKIP_MPICXX=1 -s -o Faddeeva_w.oct Faddeeva_w_oct.cc Faddeeva_w.cc
- Python: Our code is used to provide
scipy.special.wofzin SciPy starting in version 0.12.0 (see here).
Algorithm
This implementation uses a combination of different algorithms, centering around computing the Faddeeva function w(z). For sufficiently large |z|, we use a continued-fraction expansion for w(z) similar to those described in
- Walter Gautschi, "Efficient computation of the complex error function," SIAM J. Numer. Anal. 7 (1), pp. 187–198 (1970). G. P. M. Poppe and C. M. J. Wijers, "More efficient computation of the complex error function," ACM Trans. Math. Soft. 16 (1), pp. 38–46 (1990); this is TOMS Algorithm 680.
Unlike those papers, however, we switch to a completely different algorithm for smaller |z|:
- Mofreh R. Zaghloul and Ahmed N. Ali, "Algorithm 916: Computing the Faddeyeva and Voigt Functions," ACM Trans. Math. Soft. 38 (2), 15 (2011). Preprint available at arXiv:1106.0151.
(I initially used this algorithm for all z, but the continued-fraction expansion turned out to be faster for larger |z|. On the other hand, Algorithm 916 is competitive or faster for smaller |z|, and appears to be significantly more accurate than the Poppe & Wijers code in some regions, e.g. in the vicinity of |z|=1 [although comparison with other compilers suggests that this may be a problem specific to gfortran]. Algorithm 916 also has better relative accuracy in Re[z] for some regions near the real-z axis. You can switch back to using Algorithm 916 for all z by changing USE_CONTINUED_FRACTION to 0 in the code.)
Note that this is SGJ's independent re-implementation of these algorithms, based on the descriptions in the papers only. In particular, we did not refer to the authors' Fortran or Matlab implementations (respectively), which are under restrictive "semifree" ACM copyright terms and are therefore unusable in free/open-source software.
Algorithm 916 requires an external complementary error function erfc(x) function for real arguments x to be supplied as a subroutine. More precisely, it requires the scaled function erfcx(x) = ex2erfc(x). Here, we use an erfcx routine written by SGJ that uses a combination of two algorithms: a continued-fraction expansion for large x and a lookup table of Chebyshev polynomials for small x. (I initially used an erfcx function derived from the DERFC routine in SLATEC, modified by SGJ to compute erfcx instead of erfc, but the new erfcx routine is much faster, and also seems to be faster than the calerf rational-Chebyshev code by W. J. Cody.)
Similarly, we also implement special-case code for real-z, where the imaginary part of w is Dawson's integral. Similar to erfcx, this is also computed by a continued-fraction expansion for large |x|, a lookup table of Chebyshev polynomials for smaller |x|, and finally a Taylor expansion for very small |x|. (This seems to be faster than the dawsn function in the Cephes library, and is substantially faster than the gsl_sf_dawson function in the GNU Scientific Library.)
The other error functions can be computed in terms of w(z). The basic equations are:
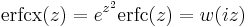 (scaled complementary error function)
(scaled complementary error function)
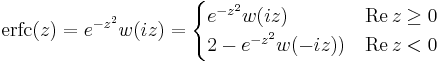 (complementary error function)
(complementary error function)
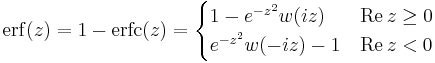 (error function)
(error function)
![\mathrm{erfi}(z) = -i\mathrm{erf}(iz) = -i[e^{z^2} w(z) - 1]](/wiki/images/math/c/d/8/cd8828edbf946b1217e0e1e2ec2e39e8.png) ; for real x,
; for real x, ![\mathrm{erfi}(x) = e^{x^2} \mathrm{Im}[w(x)] = \frac{\mathrm{Im}[w(x)]}{\mathrm{Re}[w(x)]}](/wiki/images/math/7/f/a/7fa3d04c94244398aa85d6b7bc4ffed7.png) (imaginary error function)
(imaginary error function)
![\mathrm{Dawson}(z) = \frac{\sqrt{\pi}}{2} e^{-z^2} \mathrm{erfi}(z) = \frac{i\sqrt{\pi}}{2} \left[ e^{-z^2} - w(z) \right]](/wiki/images/math/f/d/d/fdd87d27d5573db1ed44a04e00213663.png) ; for real x,
; for real x, ![F(x) = \frac{\sqrt{\pi}}{2}\mathrm{Im}[w(x)]](/wiki/images/math/2/0/7/207a2557c38b0a38f54c8316db45a399.png) (Dawson function)
(Dawson function)
In the case of erf and erfc, we employ different equations for positive and negative Re(z) in order to avoid numerical problems arising from multiplying exponentially large and small quantities. For erfi and the Dawson function, there are simplifications that occur for real x as noted. In some cases, however, there are additional complications that require our implementation to go beyond these simple formulas. For erf, large cancellation errors occur in these formulas near |z|=0 where w(z) is nearly 1, as well as near the imaginary axis for Re[erf], and in these regimes we switch to a Taylor expansion. Similarly, for the Dawson function we switch to a Taylor expansion near the origin or near the real axis. (Similar problems occur for erfi, but our erfi implementation simply calls our erf code.)
Test program
To test the code, a small test program is included at the end of Faddeeva.cc which tests w(z) against several known results (from Wolfram Alpha) and prints the relative errors obtained. To compile the test program, #define TEST_FADDEEVA in the file (or compile with -DTEST_FADDEEVA on Unix) and compile Faddeeva.cc. The resulting program prints SUCCESS at the end of its output if the errors were acceptable.
License
The software is distributed under the "MIT License", a simple permissive free/open-source license:
- Copyright © 2012 Massachusetts Institute of Technology
- Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:
- The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
- THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.
