Faddeeva Package
From AbInitio
| Revision as of 05:06, 31 October 2012 (edit) Stevenj (Talk | contribs) (→Usage) ← Previous diff |
Revision as of 05:06, 31 October 2012 (edit) Stevenj (Talk | contribs) (→Usage) Next diff → |
||
| Line 31: | Line 31: | ||
| extern double ImFaddeeva_w(double x); | extern double ImFaddeeva_w(double x); | ||
| - | which computes Im[''w''(''x'')]. | + | which computes Im[''w''(''x'')] efficiently. |
| == Wrappers: Matlab, GNU Octave, and Python == | == Wrappers: Matlab, GNU Octave, and Python == | ||
Revision as of 05:06, 31 October 2012
Contents |
Faddeeva / complex error function
Steven G. Johnson has written free/open-source C++ code (with wrappers for other languages) to compute the scaled complex error function w(z) = e−z2erfc(−iz), also called the Faddeeva function (and also the plasma dispersion function), for arbitrary complex arguments z to a given accuracy. Download the source code from:
- http://ab-initio.mit.edu/Faddeeva_w.cc (updated 30 October 2012)
Given the Faddeeva function, one can easily compute Voigt functions, the Dawson function, and similar related functions. Our implementation includes special-case optimizations for purely real or imaginary z, making the performance competitive with specialized implementations of the Dawson function, erfcx, and erfi.
Usage
To use the code, add the following declaration to your C++ source (or header file):
#include <complex> extern std::complex<double> Faddeeva_w(std::complex<double> z, double relerr=0);
The function Faddeeva_w(z, relerr) computes w(z) to a desired relative error relerr.
Omitting the relerr argument, or passing relerr=0 (or any relerr less than machine precision ε≈10−16), corresponds to requesting machine precision, and in practice a relative error < 10−13 is usually achieved. Specifying a larger value of relerr may improve performance (at the expense of accuracy).
You should also compile Faddeeva_w.cc and link it with your program, of course.
In terms of w(z), some other important functions are:
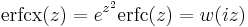 (scaled complementary error function)
(scaled complementary error function)
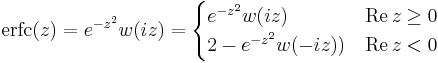 (complementary error function)
(complementary error function)
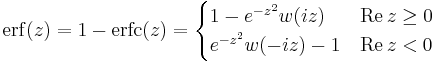 (error function)
(error function)
![\mathrm{erfi}(z) = -i\mathrm{erf}(iz) = -i[e^{z^2} w(z) - 1]](/wiki/images/math/c/d/8/cd8828edbf946b1217e0e1e2ec2e39e8.png) ; for real x,
; for real x, ![\mathrm{erfi}(x) = e^{x^2} \mathrm{Im}[w(x)] = \frac{\mathrm{Im}[w(x)]}{\mathrm{Re}[w(x)]}](/wiki/images/math/7/f/a/7fa3d04c94244398aa85d6b7bc4ffed7.png) (imaginary error function)
(imaginary error function)
![F(z) = \frac{i\sqrt{\pi}}{2} \left[ e^{-z^2} - w(z) \right]](/wiki/images/math/a/2/1/a21ad27f78f1afdd2c74ab584e19cf41.png) ; for real x,
; for real x, ![F(x) = \frac{\sqrt{\pi}}{2}\mathrm{Im}[w(x)]](/wiki/images/math/2/0/7/207a2557c38b0a38f54c8316db45a399.png) (Dawson function)
(Dawson function)
Note that in the case of erf and erfc, we provide different equations for positive and negative Re(z), in order to avoid numerical problems arising from multiplying exponentially large and small quantities. For erfi and F, there are simplifications that occur for real x as noted. Furthermore, if you want to compute the Dawson function F for real z=x, you can obtain the imaginary part of w(x) directly without computing the real part, by calling:
extern double ImFaddeeva_w(double x);
which computes Im[w(x)] efficiently.
Wrappers: Matlab, GNU Octave, and Python
Wrappers are available for this function in other languages.
- Matlab (also available here): A function
Faddeeva_w(z, relerr), where the arguments have the same meaning as above (therelerrargument is optional) can be downloaded from Faddeeva_w_mex.cc (along with the help file Faddeeva_w.m. Compile it into an octave plugin with:
mex -output Faddeeva_w -O Faddeeva_w_mex.cc Faddeeva_w.cc
- GNU Octave: A function
Faddeeva_w(z, relerr), where the arguments have the same meaning as above (therelerrargument is optional) can be downloaded from Faddeeva_w_oct.cc. Compile it into a MEX file with:
mkoctfile -DMPICH_SKIP_MPICXX=1 -DOMPI_SKIP_MPICXX=1 -s -o Faddeeva_w.oct Faddeeva_w_oct.cc Faddeeva_w.cc
- Python: Our code is used to provide
scipy.special.wofzin SciPy starting in version 0.12.0 (see here).
Algorithm
This implementation uses a combination of different algorithms. For sufficiently large |z|, we use a continued-fraction expansion for w(z) similar to those described in
- Walter Gautschi, "Efficient computation of the complex error function," SIAM J. Numer. Anal. 7 (1), pp. 187–198 (1970). G. P. M. Poppe and C. M. J. Wijers, "More efficient computation of the complex error function," ACM Trans. Math. Soft. 16 (1), pp. 38–46 (1990); this is TOMS Algorithm 680.
Unlike those papers, however, we switch to a completely different algorithm for smaller |z|:
- Mofreh R. Zaghloul and Ahmed N. Ali, "Algorithm 916: Computing the Faddeyeva and Voigt Functions," ACM Trans. Math. Soft. 38 (2), 15 (2011). Preprint available at arXiv:1106.0151.
(I initially used this algorithm for all z, but the continued-fraction expansion turned out to be faster for larger |z|. On the other hand, Algorithm 916 is competitive or faster for smaller |z|, and appears to be significantly more accurate than the Poppe & Wijers code in some regions, e.g. in the vicinity of |z|=1 [although comparison with other compilers suggests that this may be a problem specific to gfortran]. Algorithm 916 also has better relative accuracy in Re[z] for some regions near the real-z axis. You can switch back to using Algorithm 916 for all z by changing USE_CONTINUED_FRACTION to 0 in the code.)
Note that this is SGJ's independent re-implementation of these algorithms, based on the descriptions in the papers only. In particular, we did not refer to the authors' Fortran or Matlab implementations (respectively), which are under restrictive "semifree" ACM copyright terms and are therefore unusable in free/open-source software.
Algorithm 916 requires an external complementary error function erfc(x) function for real arguments x to be supplied as a subroutine. More precisely, it requires the scaled function erfcx(x) = ex2erfc(x). Here, we use an erfcx routine written by SGJ that uses a combination of two algorithms: a continued-fraction expansion for large x and a lookup table of Chebyshev polynomials for small x. (I initially used an erfcx function derived from the DERFC routine in SLATEC, modified by SGJ to compute erfcx instead of erfc, by the new erfcx routine is much faster.)
Similarly, we also implement special-case code for real-z, where the imaginary part of w is Dawson's integral. Like erfcx, this is also computed by a continued-fraction expansion for large |x|, a lookup table of Chebyshev polynomials for small |x|, and finally a Taylor expansion for very small |x|.
Test program
To test the code, a small test program is included at the end of Faddeeva_w.cc which tests w(z) against several known results (from Wolfram Alpha) and prints the relative errors obtained. To compile the test program, #define FADDEEVA_W_TEST in the file (or compile with -DFADDEEVA_W_TEST on Unix) and compile Faddeeva_w.cc. The resulting program prints SUCCESS at the end of its output if the errors were acceptable.
License
The software is distributed under the "MIT License", a simple permissive free/open-source license:
- Copyright © 2012 Massachusetts Institute of Technology
- Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:
- The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
- THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.
