Faddeeva Package
From AbInitio
| Revision as of 03:25, 4 November 2012 (edit) Stevenj (Talk | contribs) (Faddeeva w moved to Faddeeva Package) ← Previous diff |
Current revision (00:41, 17 April 2017) (edit) Stevenj (Talk | contribs) (→Download) |
||
| Line 1: | Line 1: | ||
| - | = Complex error functions = | + | [http://math.mit.edu/~stevenj Steven G. Johnson] has written [[w:Free and open-source software|free/open-source]] C++ code (with wrappers for C, Matlab, GNU Octave, Python, R, Scilab, and Julia) to compute the various [[w:Error function|error functions]] of arbitrary [[w:Complex number|complex]] arguments. In particular, we provide: |
| - | [http://math.mit.edu/~stevenj Steven G. Johnson] has written [[w:Free and open-source software|free/open-source]] C++ code (with wrappers for other languages) to compute the various [[w:Error function|error functions]] of arbitrary [[w:Complex number|complex]] arguments. In particular, we provide: | + | * '''w''', the [[w:Faddeeva function|Faddeeva function]] <math>w(z) = e^{-z^2} \mathrm{erfc}(-iz) \! </math>, where erfc is the complementary error function. |
| + | * '''erf''', the [[w:Error function|error function]] <math>\mathrm{erf}(z) \!</math> | ||
| + | * '''erfc''', the complementary error function <math>\mathrm{erfc}(z) = 1 - \mathrm{erf}(z) \! </math> | ||
| + | * '''erfcx''', the scaled complementary error function <math>\mathrm{erfcx}(z) = e^{z^2} \mathrm{erfc}(z) = w(iz) \! </math> | ||
| + | * '''erfi''', the imaginary error function <math>\mathrm{erfi}(z) = -i \mathrm{erf}(iz) \!</math> | ||
| + | * '''Dawson''', the [[w:Dawson function|Dawson function]] <math>\mathrm{Dawson}(z) = \frac{\sqrt{\pi}}{2} e^{-z^2} \mathrm{erfi}(z)</math> | ||
| - | * The [[w:Faddeeva function|Faddeeva function]] <math>w(z) = e^{-z^2} \mathrm{erfc}(z) \!</math>, where erfc is the complementary error function. | + | Given the Faddeeva function ''w''(''z'') and the other complex error functions, one can also easily compute [[w:Voigt profile|Voigt functions]], [[w:Fresnel integral|Fresnel integrals]], and similar related functions as well. In benchmarks of our code, we find that it is comparable to or faster than most competing software for these functions in the complex plane (but we also have special-case optimizations for purely real or imaginary arguments), and we find that the accuracy is typically at at least 13 [[w:Significant figures|significant digits]] in both the real and imaginary parts. |
| - | * The [[w:Error function|error function]] <math>\mathrm{erf}(z) \!</math> | + | |
| - | * The complementary error function <math>\mathrm{erfc}(z) = 1 - \mathrm{erf}(z) \!</math> | + | |
| - | * The scaled complementary error function <math>\mathrm{erfcx}(z) = e^{z^2} \mathrm{erfc}(z) \!</math> | + | |
| - | * The imaginary error function <math>\mathrm{erfi}(z) = -i \mathrm{erf}(iz) \!</math> | + | |
| - | * The [[w:Dawson function|Dawson function]] <math>\mathrm{Dawson}(z) = \frac{\sqrt{\pi}}{2} e^{-z^2} \mathrm{erfi}(z)</math> | + | |
| - | Given the Faddeeva function ''w''(''z''), one can also easily compute [[w:Voigt profile|Voigt functions]] and similar related functions as well. In benchmarks of our code, we find that it is competitive or faster than most competing software for these functions, especially in the complex plane (but we also have special-case optimizations for purely real or imaginary arguments), and we find that the accuracy is typically near [[w:Machine epsilon|machine precision]]. | + | Because all of the algorithms are based on algorithms for the Faddeeva function, we call this the '''Faddeeva Package'''. |
| - | Because all of the algorithms are based on algorithms for the Faddeeva function, we call this the '''Faddeeva package'''. Download the source code from: | + | ==Download== |
| - | * [http://ab-initio.mit.edu/Faddeeva.cc http://ab-initio.mit.edu/Faddeeva.cc] and [http://ab-initio.mit.edu/Faddeeva.hh http://ab-initio.mit.edu/Faddeeva.hh] (updated 3 November 2012) | + | Download the source code from: |
| + | |||
| + | * [http://ab-initio.mit.edu/Faddeeva.cc http://ab-initio.mit.edu/Faddeeva.cc] and [http://ab-initio.mit.edu/Faddeeva.hh http://ab-initio.mit.edu/Faddeeva.hh] for C++, or Faddeeva.cc and [http://ab-initio.mit.edu/Faddeeva.h http://ab-initio.mit.edu/Faddeeva.h] for C (requires a C99-compatible compiler) (updated 12 May 2015) | ||
| + | |||
| + | See also below for wrappers to call the Faddeeva package from other languages. This code has also been packaged into the [http://apps.jcns.fz-juelich.de/libcerf libcerf] and [https://github.com/JuliaLang/openlibm openlibm] libraries. | ||
| == Usage == | == Usage == | ||
| Line 26: | Line 30: | ||
| extern std::complex<double> Faddeeva::w(std::complex<double> z, double relerr=0); | extern std::complex<double> Faddeeva::w(std::complex<double> z, double relerr=0); | ||
| - | The function <code>Faddeeva::w(z, relerr)</code> computes ''w''(''z'') to a desired [[w:Approximation error|relative error]] <code>relerr</code>. | + | This function <code>Faddeeva::w(z, relerr)</code> computes ''w''(''z'') to a desired [[w:Approximation error|relative error]] <code>relerr</code>. |
| - | Omitting the <code>relerr</code> argument, or passing <code>relerr=0</code> (or any <code>relerr</code> less than machine precision ε≈10<sup>−16</sup>), corresponds to requesting [[w:Machine epsilon|machine precision]], and in practice a relative error < 10<sup>−13</sup> is usually achieved. Specifying a larger value of <code>relerr</code> may improve performance (at the expense of accuracy). | + | Omitting the <code>relerr</code> argument, or passing <code>relerr=0</code> (or any <code>relerr</code> less than machine precision ε≈10<sup>−16</sup>), corresponds to requesting [[w:Machine epsilon|machine precision]], and in practice a relative error < 10<sup>−13</sup> is usually achieved. Specifying a larger value of <code>relerr</code> may improve performance for some ''z'' (at the expense of accuracy). |
| Similarly, the erf, erfc, erfcx, erfi, and Dawson functions are computed by calling: | Similarly, the erf, erfc, erfcx, erfi, and Dawson functions are computed by calling: | ||
| Line 48: | Line 52: | ||
| (These functions always compute to maximum accuracy, usually near machine precision.) | (These functions always compute to maximum accuracy, usually near machine precision.) | ||
| - | It is also sometimes useful to compute Im[''w''(''x'')] for real ''x'', since <math>\mathrm{Im}[w(z)] = e^{-z^2} \mathrm{erfi}(z)</math>. Note that Re[''w''(''x'')] is simply exp(−''x''<sup>2</sup>) for real ''x''. Im[''w''(''x'')] can be computed efficiently by calling: | + | It is also sometimes useful to compute Im[''w''(''x'')] for real ''x'', since <math>\mathrm{Im}[w(x)] = e^{-x^2} \mathrm{erfi}(x)</math> in that case (like the Dawson function but without the √π/2 factor). [Note that Re[''w''(''x'')] is simply exp(−''x''<sup>2</sup>) for real ''x''.] Im[''w''(''x'')] can be computed efficiently to nearly machine precision by calling: |
| extern double Faddeeva::w_im(double x); | extern double Faddeeva::w_im(double x); | ||
| - | (Again, this computes to nearly machine precision.) | + | == Wrappers: C, Matlab, GNU Octave, Python, R, Scilab, Julia == |
| - | + | ||
| - | == Wrappers: Matlab, GNU Octave, and Python == | + | |
| Wrappers are available for this function in other languages. | Wrappers are available for this function in other languages. | ||
| - | * [[w:MATLAB|Matlab]] (also available [http://www.mathworks.com/matlabcentral/fileexchange/38787-faddeeva-function-scaled-complex-error-function here]): A function <code>Faddeeva_w(z, relerr)</code>, where the arguments have the same meaning as above (the <code>relerr</code> argument is optional) can be downloaded from [http://ab-initio.mit.edu/Faddeeva_w_mex.cc Faddeeva_w_mex.cc] (along with the help file [http://ab-initio.mit.edu/Faddeeva_w.m Faddeeva_w.m]. Compile it into an octave plugin with: | + | * [[w:C (programming language)|C]]: Download the files [http://ab-initio.mit.edu/Faddeeva.c http://ab-initio.mit.edu/Faddeeva.c] and [http://ab-initio.mit.edu/Faddeeva.h http://ab-initio.mit.edu/Faddeeva.h] (in ''addition'' to [http://ab-initio.mit.edu/Faddeeva.cc Faddeeva.cc] from above) to obtain a pure C version (you do ''not'' need a C++ compiler), using [[w:C99|C99]] complex numbers. The complex functions are <code>Faddeeva_erf(double complex z, double relerr)</code> etc. instead of <code>Faddeeva::erf</code>, and the real-argument versions are <code>Faddeeva_erf_re(double x)</code> etc. (Note that in [[w:GNU Compiler Collection|gcc]] you may need to compile with the <code>-std=c99</code> flag to enable C99 support.) |
| + | * [[w:MATLAB|Matlab]] (also available [http://www.mathworks.com/matlabcentral/fileexchange/38787 here]): We provide source code for compiled Matlab plugins ([[w:MEX file|MEX files]]) to interface all of the error functions above from Matlab. | ||
| + | ** Download the code and documentation from: [http://ab-initio.mit.edu/Faddeeva-MATLAB.zip http://ab-initio.mit.edu/Faddeeva-MATLAB.zip] (a [[w:Zip (file format)|zip file]]) | ||
| + | ** The provided functions are called <code>Faddeeva_w</code>, <code>Faddeeva_erf</code>, <code>Faddeeva_erfc</code>, <code>Faddeeva_erfi</code>, <code>Faddeeva_erfcx</code>, and <code>Faddeeva_Dawson</code>, equivalent to the C++ functions above. All have usage of the form <code>w = Faddeeva_w(z)</code> [or <code>w = Faddeeva_w(z, relerr)</code> to pass the optional relative error], to compute the function value from an array or matrix <code>z</code> of complex (or real) inputs. | ||
| + | ** For convenience, a script to compile all of the plugins using the [http://www.mathworks.com/help/matlab/ref/mex.html mex command] in Matlab is included. Assuming you have a C++ compiler installed (and have run <code>mex -setup</code> to tell Matlab to use it), you can simply run the <code>Faddeeva_build.m</code> script in Matlab to compile all of the Faddeeva functions. | ||
| + | ** Install the resulting <code>*.mex*</code> files, along with the <code>*.m</code> help files, into your [http://www.mathworks.com/help/matlab/ref/path.html Matlab path] | ||
| + | |||
| + | * [[w:GNU Octave|GNU Octave]]: Similar to Matlab, above, we provide source code for compiled GNU Octave plugins ([http://www.gnu.org/software/octave/doc/interpreter/Oct_002dFiles.html .oct files]) for all of the error functions above. (''Note:'' our code for complex-argument erf, erfc, erfcx, erfi, and dawson functions has been [http://hg.savannah.gnu.org/hgweb/octave/graph/9811b32b645e merged into Octave] and should be included in a future release.) | ||
| + | ** Download the code and documentation from: [http://ab-initio.mit.edu/Faddeeva-octave.tgz http://ab-initio.mit.edu/Faddeeva-octave.tgz] (a [[w:gzip|gzipped]] [[w:tar (file format)|tar file]]) | ||
| + | ** The provided functions are called <code>Faddeeva_w</code>, <code>Faddeeva_erf</code>, <code>Faddeeva_erfc</code>, <code>Faddeeva_erfi</code>, <code>Faddeeva_erfcx</code>, and <code>Faddeeva_Dawson</code>, with usage identical to the Matlab plugins above. | ||
| + | ** A [[w:Make (software)|Makefile]] is included. Assuming you have a C++ compiler and the <code>mkoctfile</code> command installed (<code>mkoctfile</code> comes with Octave, possibly in an <code>octave-devel</code> or similarly named package in GNU/Linux distributions), you can simply run <code>make</code> to compile the plugins, and <code>[[w:sudo|sudo]] make install</code> to install them system-wide (assuming you have system administrator privileges); otherwise put the compiled <code>.oct</code> files somewhere in your [http://www.gnu.org/software/octave/doc/interpreter/Manipulating-the-load-path.html octave path]. | ||
| + | |||
| + | * [[w:Python (programming language)|Python]]: Our code is used to provide <code>scipy.special.erf</code>, <code>scipy.special.wofz</code>, and the other error functions in [[w:SciPy|SciPy]] starting in version 0.12.0 (see [https://github.com/scipy/scipy/commit/ed14bf0 here]). | ||
| - | mex -output Faddeeva_w -O Faddeeva_w_mex.cc Faddeeva_w.cc | + | * [[w:R (programming language)|R]]: Baptiste Auguié and Dirk Eddelbuettel have written an R interface to the Faddeeva package, [https://github.com/baptiste/rcppfaddeeva available on Github] and [http://cran.r-project.org/web/packages/RcppFaddeeva/index.html on CRAN]. |
| - | * [[w:GNU Octave|GNU Octave]]: A function <code>Faddeeva_w(z, relerr)</code>, where the arguments have the same meaning as above (the <code>relerr</code> argument is optional) can be downloaded from [http://ab-initio.mit.edu/Faddeeva_w_oct.cc Faddeeva_w_oct.cc]. Compile it into a [[w:MEX file|MEX file]] with: | + | * [[w:Scilab|Scilab]] has [http://bugzilla.scilab.org/show_bug.cgi?id=6092 incorporated] this code to implement complex error functions (and related functions) in [http://docs.scipy.org/doc/scipy-dev/reference/release.0.12.0.html SciPy version 0.12]. |
| - | mkoctfile [http://bugs.debian.org/cgi-bin/bugreport.cgi?bug=686926 -DMPICH_SKIP_MPICXX=1 -DOMPI_SKIP_MPICXX=1] -s -o Faddeeva_w.oct Faddeeva_w_oct.cc Faddeeva_w.cc | + | * [http://julialang.org/ Julia] uses the Faddeeva Package to provide its complex <code>erf</code>, <code>erfc</code>, <code>erfcx</code>, <code>erfi</code>, and <code>dawson</code> functions. |
| - | * [[w:Python (programming language)|Python]]: Our code is used to provide <code>scipy.special.wofz</code> in [[w:SciPy|SciPy]] starting in version 0.12.0 (see [http://projects.scipy.org/scipy/ticket/1741 here]). | + | == Algorithms == |
| - | == Algorithm == | + | Our implementation uses a combination of different algorithms, mostly centering around computing the Faddeeva function ''w''(''z''). |
| - | This implementation uses a combination of different algorithms, centering around computing the Faddeeva function ''w''(''z''). For sufficiently large |''z''|, we use a continued-fraction expansion for ''w''(''z'') similar to those described in | + | To compute the Faddeeva function for sufficiently large |''z''|, we use a continued-fraction expansion for ''w''(''z'') similar to those described in |
| * Walter Gautschi, "[http://dx.doi.org/10.1137/0707012 Efficient computation of the complex error function]," ''SIAM J. Numer. Anal.'' '''7''' (1), pp. 187–198 (1970). G. P. M. Poppe and C. M. J. Wijers, "[http://dx.doi.org/10.1145/77626.77629 More efficient computation of the complex error function]," ''ACM Trans. Math. Soft.'' '''16''' (1), pp. 38–46 (1990); this is [http://www.netlib.org/toms/680 TOMS Algorithm 680]. | * Walter Gautschi, "[http://dx.doi.org/10.1137/0707012 Efficient computation of the complex error function]," ''SIAM J. Numer. Anal.'' '''7''' (1), pp. 187–198 (1970). G. P. M. Poppe and C. M. J. Wijers, "[http://dx.doi.org/10.1145/77626.77629 More efficient computation of the complex error function]," ''ACM Trans. Math. Soft.'' '''16''' (1), pp. 38–46 (1990); this is [http://www.netlib.org/toms/680 TOMS Algorithm 680]. | ||
| - | Unlike those papers, however, we switch to a completely different algorithm for smaller |''z''|: | + | Unlike those papers, however, we switch to a completely different algorithm for smaller |''z''| or for ''z'' close to the real axis: |
| * Mofreh R. Zaghloul and Ahmed N. Ali, "[http://dx.doi.org/10.1145/2049673.2049679 Algorithm 916: Computing the Faddeyeva and Voigt Functions]," ''ACM Trans. Math. Soft.'' '''38''' (2), 15 (2011). Preprint available at [http://arxiv.org/abs/1106.0151 arXiv:1106.0151]. | * Mofreh R. Zaghloul and Ahmed N. Ali, "[http://dx.doi.org/10.1145/2049673.2049679 Algorithm 916: Computing the Faddeyeva and Voigt Functions]," ''ACM Trans. Math. Soft.'' '''38''' (2), 15 (2011). Preprint available at [http://arxiv.org/abs/1106.0151 arXiv:1106.0151]. | ||
| Line 84: | Line 98: | ||
| Algorithm 916 requires an external [[w:Error function|complementary error function]] erfc(''x'') function for ''real'' arguments ''x'' to be supplied as a subroutine. More precisely, it requires the scaled function erfcx(''x'') = ''e''<sup>''x''<sup>2</sup></sup>erfc(''x''). Here, we use an erfcx routine written by SGJ that uses a combination of two algorithms: a continued-fraction expansion for large ''x'' and a lookup table of Chebyshev polynomials for small ''x''. (I initially used an erfcx function derived from the DERFC routine in [[w:SLATEC|SLATEC]], modified by SGJ to compute erfcx instead of erfc, but the new erfcx routine is much faster, and also seems to be faster than the [http://www.netlib.org/specfun/erf calerf] rational-Chebyshev code by W. J. Cody.) | Algorithm 916 requires an external [[w:Error function|complementary error function]] erfc(''x'') function for ''real'' arguments ''x'' to be supplied as a subroutine. More precisely, it requires the scaled function erfcx(''x'') = ''e''<sup>''x''<sup>2</sup></sup>erfc(''x''). Here, we use an erfcx routine written by SGJ that uses a combination of two algorithms: a continued-fraction expansion for large ''x'' and a lookup table of Chebyshev polynomials for small ''x''. (I initially used an erfcx function derived from the DERFC routine in [[w:SLATEC|SLATEC]], modified by SGJ to compute erfcx instead of erfc, but the new erfcx routine is much faster, and also seems to be faster than the [http://www.netlib.org/specfun/erf calerf] rational-Chebyshev code by W. J. Cody.) | ||
| - | Similarly, we also implement special-case code for real-''z'', where the imaginary part of ''w'' is Dawson's integral. Similar to erfcx, this is also computed by a continued-fraction expansion for large |''x''|, a lookup table of Chebyshev polynomials for smaller |''x''|, and finally a Taylor expansion for very small |''x''|. (This seems to be faster than the [http://www.netlib.org/cephes/doubldoc.html#dawsn dawsn function] in the Cephes library, and is substantially faster than the [http://www.gnu.org/software/gsl/manual/html_node/Dawson-Function.html gsl_sf_dawson] function in the [[w:GNU Scientific Library|GNU Scientific Library]].) | + | Similarly, we also implement special-case code for real ''z'', where the imaginary part of ''w'' is Dawson's integral. Similar to erfcx, this is also computed by a continued-fraction expansion for large |''x''|, a lookup table of Chebyshev polynomials for smaller |''x''|, and finally a Taylor expansion for very small |''x''|. (This seems to be faster than the [http://www.netlib.org/cephes/doubldoc.html#dawsn dawsn function] in the Cephes library, and is substantially faster than the [http://www.gnu.org/software/gsl/manual/html_node/Dawson-Function.html gsl_sf_dawson] function in the [[w:GNU Scientific Library|GNU Scientific Library]].) |
| The other error functions can be computed in terms of ''w''(''z''). The basic equations are: | The other error functions can be computed in terms of ''w''(''z''). The basic equations are: | ||
| Line 90: | Line 104: | ||
| :<math>\mathrm{erfc}(z) = e^{-z^2} w(iz) = \begin{cases} e^{-z^2} w(iz) & \mathrm{Re}\,z \geq 0 \\ 2 - e^{-z^2} w(-iz)) & \mathrm{Re}\,z < 0 \end{cases}</math> (complementary error function) | :<math>\mathrm{erfc}(z) = e^{-z^2} w(iz) = \begin{cases} e^{-z^2} w(iz) & \mathrm{Re}\,z \geq 0 \\ 2 - e^{-z^2} w(-iz)) & \mathrm{Re}\,z < 0 \end{cases}</math> (complementary error function) | ||
| :<math>\mathrm{erf}(z) = 1 - \mathrm{erfc}(z) = \begin{cases} 1 - e^{-z^2} w(iz) & \mathrm{Re}\,z \geq 0 \\ e^{-z^2} w(-iz) - 1 & \mathrm{Re}\,z < 0 \end{cases}</math> (error function) | :<math>\mathrm{erf}(z) = 1 - \mathrm{erfc}(z) = \begin{cases} 1 - e^{-z^2} w(iz) & \mathrm{Re}\,z \geq 0 \\ e^{-z^2} w(-iz) - 1 & \mathrm{Re}\,z < 0 \end{cases}</math> (error function) | ||
| - | :<math>\mathrm{erfi}(z) = -i\mathrm{erf}(iz) = -i[e^{z^2} w(z) - 1]</math>; for '''real''' ''x'', <math>\mathrm{erfi}(x) = e^{x^2} \mathrm{Im}[w(x)] = \frac{\mathrm{Im}[w(x)]}{\mathrm{Re}[w(x)]}</math> (imaginary error function) | + | :<math>\mathrm{erfi}(z) = -i\mathrm{erf}(iz) \!</math>; for '''real''' ''x'', <math>\mathrm{erfi}(x) = e^{x^2} \mathrm{Im}[w(x)] = \frac{\mathrm{Im}[w(x)]}{\mathrm{Re}[w(x)]}</math> (imaginary error function) |
| - | :<math>\mathrm{Dawson}(z) = \frac{\sqrt{\pi}}{2} e^{-z^2} \mathrm{erfi}(z) = \frac{i\sqrt{\pi}}{2} \left[ e^{-z^2} - w(z) \right]</math>; for '''real''' ''x'', <math>F(x) = \frac{\sqrt{\pi}}{2}\mathrm{Im}[w(x)]</math> ([[w:Dawson function|Dawson function]]) | + | :<math>\mathrm{Dawson}(z) = \frac{\sqrt{\pi}}{2} e^{-z^2} \mathrm{erfi}(z) = \frac{i\sqrt{\pi}}{2} \begin{cases} e^{-z^2} - w(z) & \mathrm{Re}\,z \geq 0 \\ w(-z) - e^{-z^2} & \mathrm{Re}\,z < 0 \end{cases}</math>; for '''real''' ''x'', <math>\mathrm{Dawson}(x) = \frac{\sqrt{\pi}}{2}\mathrm{Im}[w(x)]</math> ([[w:Dawson function|Dawson function]]) |
| - | In the case of erf and erfc, we employ different equations for positive and negative Re(''z'') in order to avoid numerical problems arising from multiplying exponentially large and small quantities. For erfi and the Dawson function, there are simplifications that occur for real ''x'' as noted. In some cases, however, there are additional complications that require our implementation to go beyond these simple formulas. For erf, large cancellation errors occur in these formulas near |''z''|=0 where ''w''(''z'') is nearly 1, as well as near the imaginary axis for Re[erf], and in these regimes we switch to a Taylor expansion. Similarly, for the Dawson function we switch to a Taylor expansion near the origin or near the real axis. (Similar problems occur for erfi, but our erfi implementation simply calls our erf code.) | + | Note that we sometimes employ different equations for positive and negative Re(''z'') in order to avoid numerical problems arising from multiplying exponentially large and small quantities. For erfi and the Dawson function, there are simplifications that occur for real ''x'' as noted. In some cases, however, there are additional complications that require our implementation to go beyond these simple formulas. For erf, large cancellation errors occur in these formulas near |''z''|=0 where ''w''(''z'') is nearly 1, as well as near the imaginary axis for Re[erf], and in these regimes we switch to a Taylor expansion. Similarly, for the Dawson function we switch to a Taylor expansion near the origin or near the real axis. (Similar problems occur for erfi, but our erfi implementation simply calls our erf code.) |
| == Test program == | == Test program == | ||
| Line 100: | Line 114: | ||
| == License == | == License == | ||
| - | The software is distributed under the "[[w:MIT License|MIT License]]", a simple permissive free/open-source license: | + | The software is distributed under the "[[w:MIT License|MIT License]]" (also called the ''Expat License''), a simple permissive free/open-source license (which is [http://www.gnu.org/licenses/license-list.html#Expat compatible with the GPL and most other licenses]): |
| :''Copyright © 2012 Massachusetts Institute of Technology'' | :''Copyright © 2012 Massachusetts Institute of Technology'' | ||
Current revision
Steven G. Johnson has written free/open-source C++ code (with wrappers for C, Matlab, GNU Octave, Python, R, Scilab, and Julia) to compute the various error functions of arbitrary complex arguments. In particular, we provide:
- w, the Faddeeva function
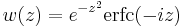 , where erfc is the complementary error function.
, where erfc is the complementary error function.
- erf, the error function
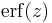
- erfc, the complementary error function
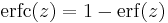
- erfcx, the scaled complementary error function
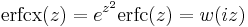
- erfi, the imaginary error function
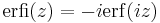
- Dawson, the Dawson function
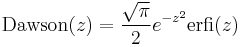
Given the Faddeeva function w(z) and the other complex error functions, one can also easily compute Voigt functions, Fresnel integrals, and similar related functions as well. In benchmarks of our code, we find that it is comparable to or faster than most competing software for these functions in the complex plane (but we also have special-case optimizations for purely real or imaginary arguments), and we find that the accuracy is typically at at least 13 significant digits in both the real and imaginary parts.
Because all of the algorithms are based on algorithms for the Faddeeva function, we call this the Faddeeva Package.
Contents |
Download
Download the source code from:
- http://ab-initio.mit.edu/Faddeeva.cc and http://ab-initio.mit.edu/Faddeeva.hh for C++, or Faddeeva.cc and http://ab-initio.mit.edu/Faddeeva.h for C (requires a C99-compatible compiler) (updated 12 May 2015)
See also below for wrappers to call the Faddeeva package from other languages. This code has also been packaged into the libcerf and openlibm libraries.
Usage
To use the code, include the Faddeeva.hh header file:
#include "Faddeeva.hh"
and compile and link the Faddeeva.cc source code. You can then call various functions. For example:
extern std::complex<double> Faddeeva::w(std::complex<double> z, double relerr=0);
This function Faddeeva::w(z, relerr) computes w(z) to a desired relative error relerr.
Omitting the relerr argument, or passing relerr=0 (or any relerr less than machine precision ε≈10−16), corresponds to requesting machine precision, and in practice a relative error < 10−13 is usually achieved. Specifying a larger value of relerr may improve performance for some z (at the expense of accuracy).
Similarly, the erf, erfc, erfcx, erfi, and Dawson functions are computed by calling:
extern std::complex<double> Faddeeva::erf(std::complex<double> z, double relerr=0); extern std::complex<double> Faddeeva::erfc(std::complex<double> z, double relerr=0); extern std::complex<double> Faddeeva::erfcx(std::complex<double> z, double relerr=0); extern std::complex<double> Faddeeva::erfi(std::complex<double> z, double relerr=0); extern std::complex<double> Faddeeva::Dawson(std::complex<double> z, double relerr=0);
Since these functions are purely real for real arguments z=x, we provide the following specialized interfaces for convenience (and a slight performance gain, although the complex functions above automatically execute specialized code for purely real arguments):
extern double Faddeeva::erf(double x); extern double Faddeeva::erfc(double x); extern double Faddeeva::erfcx(double x); extern double Faddeeva::erfi(double x); extern double Faddeeva::Dawson(double x);
(These functions always compute to maximum accuracy, usually near machine precision.)
It is also sometimes useful to compute Im[w(x)] for real x, since ![\mathrm{Im}[w(x)] = e^{-x^2} \mathrm{erfi}(x)](/wiki/images/math/6/2/6/626e23afe659baf91df3e0bbebb9b1c1.png) in that case (like the Dawson function but without the √π/2 factor). [Note that Re[w(x)] is simply exp(−x2) for real x.] Im[w(x)] can be computed efficiently to nearly machine precision by calling:
in that case (like the Dawson function but without the √π/2 factor). [Note that Re[w(x)] is simply exp(−x2) for real x.] Im[w(x)] can be computed efficiently to nearly machine precision by calling:
extern double Faddeeva::w_im(double x);
Wrappers: C, Matlab, GNU Octave, Python, R, Scilab, Julia
Wrappers are available for this function in other languages.
- C: Download the files http://ab-initio.mit.edu/Faddeeva.c and http://ab-initio.mit.edu/Faddeeva.h (in addition to Faddeeva.cc from above) to obtain a pure C version (you do not need a C++ compiler), using C99 complex numbers. The complex functions are
Faddeeva_erf(double complex z, double relerr)etc. instead ofFaddeeva::erf, and the real-argument versions areFaddeeva_erf_re(double x)etc. (Note that in gcc you may need to compile with the-std=c99flag to enable C99 support.) - Matlab (also available here): We provide source code for compiled Matlab plugins (MEX files) to interface all of the error functions above from Matlab.
- Download the code and documentation from: http://ab-initio.mit.edu/Faddeeva-MATLAB.zip (a zip file)
- The provided functions are called
Faddeeva_w,Faddeeva_erf,Faddeeva_erfc,Faddeeva_erfi,Faddeeva_erfcx, andFaddeeva_Dawson, equivalent to the C++ functions above. All have usage of the formw = Faddeeva_w(z)[orw = Faddeeva_w(z, relerr)to pass the optional relative error], to compute the function value from an array or matrixzof complex (or real) inputs. - For convenience, a script to compile all of the plugins using the mex command in Matlab is included. Assuming you have a C++ compiler installed (and have run
mex -setupto tell Matlab to use it), you can simply run theFaddeeva_build.mscript in Matlab to compile all of the Faddeeva functions. - Install the resulting
*.mex*files, along with the*.mhelp files, into your Matlab path
- GNU Octave: Similar to Matlab, above, we provide source code for compiled GNU Octave plugins (.oct files) for all of the error functions above. (Note: our code for complex-argument erf, erfc, erfcx, erfi, and dawson functions has been merged into Octave and should be included in a future release.)
- Download the code and documentation from: http://ab-initio.mit.edu/Faddeeva-octave.tgz (a gzipped tar file)
- The provided functions are called
Faddeeva_w,Faddeeva_erf,Faddeeva_erfc,Faddeeva_erfi,Faddeeva_erfcx, andFaddeeva_Dawson, with usage identical to the Matlab plugins above. - A Makefile is included. Assuming you have a C++ compiler and the
mkoctfilecommand installed (mkoctfilecomes with Octave, possibly in anoctave-develor similarly named package in GNU/Linux distributions), you can simply runmaketo compile the plugins, andsudo make installto install them system-wide (assuming you have system administrator privileges); otherwise put the compiled.octfiles somewhere in your octave path.
- Python: Our code is used to provide
scipy.special.erf,scipy.special.wofz, and the other error functions in SciPy starting in version 0.12.0 (see here).
- R: Baptiste Auguié and Dirk Eddelbuettel have written an R interface to the Faddeeva package, available on Github and on CRAN.
- Scilab has incorporated this code to implement complex error functions (and related functions) in SciPy version 0.12.
- Julia uses the Faddeeva Package to provide its complex
erf,erfc,erfcx,erfi, anddawsonfunctions.
Algorithms
Our implementation uses a combination of different algorithms, mostly centering around computing the Faddeeva function w(z).
To compute the Faddeeva function for sufficiently large |z|, we use a continued-fraction expansion for w(z) similar to those described in
- Walter Gautschi, "Efficient computation of the complex error function," SIAM J. Numer. Anal. 7 (1), pp. 187–198 (1970). G. P. M. Poppe and C. M. J. Wijers, "More efficient computation of the complex error function," ACM Trans. Math. Soft. 16 (1), pp. 38–46 (1990); this is TOMS Algorithm 680.
Unlike those papers, however, we switch to a completely different algorithm for smaller |z| or for z close to the real axis:
- Mofreh R. Zaghloul and Ahmed N. Ali, "Algorithm 916: Computing the Faddeyeva and Voigt Functions," ACM Trans. Math. Soft. 38 (2), 15 (2011). Preprint available at arXiv:1106.0151.
(I initially used this algorithm for all z, but the continued-fraction expansion turned out to be faster for larger |z|. On the other hand, Algorithm 916 is competitive or faster for smaller |z|, and appears to be significantly more accurate than the Poppe & Wijers code in some regions, e.g. in the vicinity of |z|=1 [although comparison with other compilers suggests that this may be a problem specific to gfortran]. Algorithm 916 also has better relative accuracy in Re[z] for some regions near the real-z axis. You can switch back to using Algorithm 916 for all z by changing USE_CONTINUED_FRACTION to 0 in the code.)
Note that this is SGJ's independent re-implementation of these algorithms, based on the descriptions in the papers only. In particular, we did not refer to the authors' Fortran or Matlab implementations (respectively), which are under restrictive "semifree" ACM copyright terms and are therefore unusable in free/open-source software.
Algorithm 916 requires an external complementary error function erfc(x) function for real arguments x to be supplied as a subroutine. More precisely, it requires the scaled function erfcx(x) = ex2erfc(x). Here, we use an erfcx routine written by SGJ that uses a combination of two algorithms: a continued-fraction expansion for large x and a lookup table of Chebyshev polynomials for small x. (I initially used an erfcx function derived from the DERFC routine in SLATEC, modified by SGJ to compute erfcx instead of erfc, but the new erfcx routine is much faster, and also seems to be faster than the calerf rational-Chebyshev code by W. J. Cody.)
Similarly, we also implement special-case code for real z, where the imaginary part of w is Dawson's integral. Similar to erfcx, this is also computed by a continued-fraction expansion for large |x|, a lookup table of Chebyshev polynomials for smaller |x|, and finally a Taylor expansion for very small |x|. (This seems to be faster than the dawsn function in the Cephes library, and is substantially faster than the gsl_sf_dawson function in the GNU Scientific Library.)
The other error functions can be computed in terms of w(z). The basic equations are:
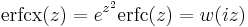 (scaled complementary error function)
(scaled complementary error function)
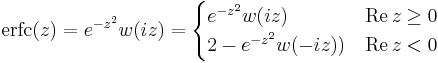 (complementary error function)
(complementary error function)
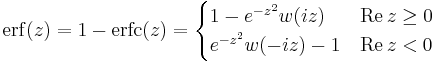 (error function)
(error function)
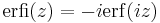 ; for real x,
; for real x, ![\mathrm{erfi}(x) = e^{x^2} \mathrm{Im}[w(x)] = \frac{\mathrm{Im}[w(x)]}{\mathrm{Re}[w(x)]}](/wiki/images/math/7/f/a/7fa3d04c94244398aa85d6b7bc4ffed7.png) (imaginary error function)
(imaginary error function)
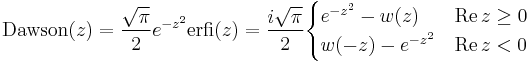 ; for real x,
; for real x, ![\mathrm{Dawson}(x) = \frac{\sqrt{\pi}}{2}\mathrm{Im}[w(x)]](/wiki/images/math/1/0/f/10f3ca7e3de96133daf1f06e48849b29.png) (Dawson function)
(Dawson function)
Note that we sometimes employ different equations for positive and negative Re(z) in order to avoid numerical problems arising from multiplying exponentially large and small quantities. For erfi and the Dawson function, there are simplifications that occur for real x as noted. In some cases, however, there are additional complications that require our implementation to go beyond these simple formulas. For erf, large cancellation errors occur in these formulas near |z|=0 where w(z) is nearly 1, as well as near the imaginary axis for Re[erf], and in these regimes we switch to a Taylor expansion. Similarly, for the Dawson function we switch to a Taylor expansion near the origin or near the real axis. (Similar problems occur for erfi, but our erfi implementation simply calls our erf code.)
Test program
To test the code, a small test program is included at the end of Faddeeva.cc which tests w(z) against several known results (from Wolfram Alpha) and prints the relative errors obtained. To compile the test program, #define TEST_FADDEEVA in the file (or compile with -DTEST_FADDEEVA on Unix) and compile Faddeeva.cc. The resulting program prints SUCCESS at the end of its output if the errors were acceptable.
License
The software is distributed under the "MIT License" (also called the Expat License), a simple permissive free/open-source license (which is compatible with the GPL and most other licenses):
- Copyright © 2012 Massachusetts Institute of Technology
- Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:
- The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
- THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.
