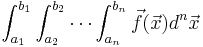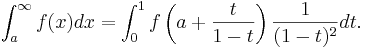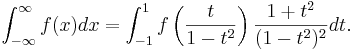Cubature (Multi-dimensional integration)
From AbInitio
| Revision as of 06:12, 17 October 2010 (edit) Stevenj (Talk | contribs) (→Cubature) ← Previous diff |
Current revision (21:06, 19 July 2017) (edit) Stevenj (Talk | contribs) (→Cubature) |
||
| Line 1: | Line 1: | ||
| == Cubature == | == Cubature == | ||
| - | [http://math.mit.edu/~stevenj Steven G. Johnson] has written a simple C subroutine for '''adaptive multidimensional integration''' (''cubature'') of '''vector-valued integrands''' over '''hypercubes''', i.e. to compute integrals of the form: | + | [http://math.mit.edu/~stevenj Steven G. Johnson] has written a simple C package for '''adaptive multidimensional integration''' (''cubature'') of '''vector-valued integrands''' over '''hypercubes''', i.e. to compute integrals of the form: |
| :<math>\int_{a_1}^{b_1}\int_{a_2}^{b_2}\cdots\int_{a_n}^{b_n} \vec{f}(\vec{x}) d^n\vec{x}</math> | :<math>\int_{a_1}^{b_1}\int_{a_2}^{b_2}\cdots\int_{a_n}^{b_n} \vec{f}(\vec{x}) d^n\vec{x}</math> | ||
| - | (Of course, it can handle scalar integrands as the special case where <math>\vec{f}</math> is a one-dimensional vector: the dimensionalities of <math>\vec{f}</math> and <math>\vec{x}</math> are independent.) The integrand can be evaluated for an '''array of points at once''' to enable '''easy parallelization'''. The code, which is distributed as '''free software''' under the terms of the [[w:GNU General Public License|GNU General Public License]] (v2 or later), is based on the algorithms described in: | + | (Of course, it can handle scalar integrands as the special case where <math>\vec{f}</math> is a one-dimensional vector: the dimensionalities of <math>\vec{f}</math> and <math>\vec{x}</math> are independent.) The integrand can be evaluated for an '''array of points at once''' to enable '''easy parallelization'''. The code, which is distributed as '''free software''' under the terms of the [[w:GNU General Public License|GNU General Public License]] (v2 or later), implements two algorithms for adaptive integration. |
| + | |||
| + | The first, ''h''-adaptive integration (recursively partitioning the integration domain into smaller subdomains, applying the same integration rule to each, until convergence is achieved), is based on the algorithms described in: | ||
| * A. C. Genz and A. A. Malik, "An adaptive algorithm for numeric integration over an N-dimensional rectangular region," ''J. Comput. Appl. Math.'' '''6''' (4), 295–302 (1980). | * A. C. Genz and A. A. Malik, "An adaptive algorithm for numeric integration over an N-dimensional rectangular region," ''J. Comput. Appl. Math.'' '''6''' (4), 295–302 (1980). | ||
| * J. Berntsen, T. O. Espelid, and A. Genz, "An adaptive algorithm for the approximate calculation of multiple integrals," ''ACM Trans. Math. Soft.'' '''17''' (4), 437–451 (1991). | * J. Berntsen, T. O. Espelid, and A. Genz, "An adaptive algorithm for the approximate calculation of multiple integrals," ''ACM Trans. Math. Soft.'' '''17''' (4), 437–451 (1991). | ||
| - | (Note that we do ''not'' use any of the original DCUHRE code by Genz, which is not under a free/open-source license.) Our code is based in part on code borrowed from the [http://mint.sbg.ac.at/HIntLib/ HIntLib numeric-integration library] by Rudolf Schürer and (for 1d integrals) from code for Gauss-Kronrod quadrature from the [http://www.gnu.org/software/gsl/ GNU Scientific Library], both of which are free software under the GNU GPL. (Another free-software multi-dimensional integration library, unrelated to our code here but also implementing the Genz–Malik algorithm among other techniques, is [http://www.feynarts.de/cuba/ Cuba].) | + | This algorithm is '''best suited for a moderate number of dimensions''' (say, < 7), and is superseded for high-dimensional integrals by other methods (e.g. [[w:Monte Carlo integration|Monte Carlo]] variants or [[w:Sparse grid|sparse grids]]). |
| - | I am also grateful to Dmitry Turbiner (dturbiner ατ alum.mit.edu), who implemented an initial prototype of the "vectorized" functionality (see below) for evaluating multiple points in a single call (as opposed to multiple functions in a single call), which facilitates parallelization of the integrand evaluation. | + | (Note that we do ''not'' use any of the original DCUHRE code by Genz, which is not under a free/open-source license.) Our code is based in part on code borrowed from the [http://mint.sbg.ac.at/HIntLib/ HIntLib numeric-integration library] by Rudolf Schürer and from code for Gauss-Kronrod quadrature (for 1d integrals) from the [http://www.gnu.org/software/gsl/ GNU Scientific Library], both of which are free software under the GNU GPL. (Another free-software multi-dimensional integration library, unrelated to our code here but also implementing the Genz–Malik algorithm among other techniques, is [http://www.feynarts.de/cuba/ Cuba].) |
| + | |||
| + | The second, ''p''-adaptive integration (repeatedly doubling the degree of the quadrature rules until convergence is achieved), is based on a tensor product of [[w:Clenshaw–Curtis quadrature|Clenshaw–Curtis quadrature]] rules. This algorithm is often superior to ''h''-adaptive integration for [[w:Smooth function|smooth]] integrands in a few (≤3) dimensions, but is a poor choice in higher dimensions or for non-smooth integrands. | ||
| + | |||
| + | For the most part, the ''p''-adaptive routines below are drop-in replacements for the ''h''-adaptive routines, with the same arguments etcetera, so you can experiment to see which one works best for your problem. One difference: the ''h''-adaptive routines do *not* evaluate the integrand on the boundaries of the integration volume, whereas the ''p''-adaptive routines *do* evaluate the integrand at the boundaries. This means that the ''p'' adaptive routines require more care in cases where there are singularities at the boundaries. | ||
| + | |||
| + | I am also grateful to Dmitry Turbiner (dturbiner ατ alum.mit.edu), who implemented an initial prototype of the "vectorized" functionality (see below) for evaluating an array of points in a single call, which facilitates parallelization of the integrand evaluation. | ||
| == Download == | == Download == | ||
| Line 18: | Line 26: | ||
| The current version of the code can be downloaded from: | The current version of the code can be downloaded from: | ||
| - | * [http://ab-initio.mit.edu/cubature/cubature-20101016.tgz cubature-20101016.tgz] | + | * [http://ab-initio.mit.edu/cubature/cubature-1.0.2.tgz cubature-1.0.2.tgz] |
| - | a [[w:gzip|gzipped]] [[w:tar (file format)|tar]] file. This unpacks to a directory containing a <code>README</code> file with instructions and a stand-alone <code>cubature.c</code> file that you can compile and link into your program, and a header file <code>cubature.h</code> that you <code>#include</code>. (The <code>cubature.c</code> code is small enough that it doesn't seem worthwhile to go to the trouble of installing it as a library.) The <code>cubature.c</code> also contains a little test program which is produced if you compile that file with <code>-DTEST_INTEGRATOR</code> (and is commented out otherwise), as described below. | + | a [[w:gzip|gzipped]] [[w:tar (file format)|tar]] file. This unpacks to a directory containing a <code>README</code> file with instructions and a stand-alone <code>hcubature.c</code> or <code>pcubature.c</code> file (along with a couple of private header files) that you can compile and link into your program for h-adaptive and p-adaptive integration, respectively, and a header file <code>cubature.h</code> that you <code>#include</code>. |
| - | B. Narasimhan wrote a [[w:GNU R|GNU R]] interface for these routines, which can be downloaded here: [http://cran.r-project.org/web/packages/cubature/index.html http://cran.r-project.org/web/packages/cubature/index.html]. | + | The <code>test.c</code> file contains a little test program which is produced if you compile that file with <code>-DHCUBATURE</code> or <code>-DPCUBATURE</code> and link with <code>hcubature.c</code> or <code>pcubature.c</code>, respectively, as described below. |
| + | |||
| + | B. Narasimhan wrote a [[w:GNU R|GNU R]] interface, which can be downloaded here: [http://cran.r-project.org/web/packages/cubature/index.html http://cran.r-project.org/web/packages/cubature/index.html]. | ||
| + | |||
| + | A [http://julialang.org/ Julia] interface can be obtained from [https://github.com/stevengj/Cubature.jl Cubature.jl]. A Python [https://github.com/saullocastro/cubature cubature.py interface] written by Saullo Castro is also available. | ||
| == Usage == | == Usage == | ||
| - | You should compile <code>cubature.c</code> and link it with your program, and <code>#include</code> the header file <code>cubature.h</code>. | + | You should compile <code>hcubature.c</code> and/or <code>pcubature.c</code> and link it with your program, and <code>#include</code> the header file <code>cubature.h</code>. |
| - | The central subroutine you will be calling is: | + | The central subroutine you will be calling for h-adaptive cubature is: |
| - | int adapt_integrate(unsigned fdim, integrand f, void *fdata, | + | int hcubature(unsigned fdim, integrand f, void *fdata, |
| - | unsigned dim, const double *xmin, const double *xmax, | + | unsigned dim, const double *xmin, const double *xmax, |
| - | unsigned maxEval, double reqAbsError, double reqRelError, | + | size_t maxEval, double reqAbsError, double reqRelError, |
| - | double *val, double *err); | + | error_norm norm, |
| + | double *val, double *err); | ||
| + | |||
| + | or <code>pcubature</code> (same arguments) for p-adaptive cubature. (See also the vectorized interface below.) | ||
| This integrates a function F(x), returning a vector of FDIM integrands, where x is a DIM-dimensional vector ranging from XMIN to XMAX (i.e. in a hypercube XMIN<sub>i</sub> ≤ x<sub>i</sub> ≤ XMAX<sub>i</sub>). | This integrates a function F(x), returning a vector of FDIM integrands, where x is a DIM-dimensional vector ranging from XMIN to XMAX (i.e. in a hypercube XMIN<sub>i</sub> ≤ x<sub>i</sub> ≤ XMAX<sub>i</sub>). | ||
| - | MAXEVAL specifies a maximum number of function evaluations (0 for no limit). Otherwise, the integration stops when the estimated |error| is less than REQABSERROR (the absolute error requested), or when the | + | MAXEVAL specifies a maximum number of function evaluations (0 for no limit). <nowiki>[</nowiki>Note: the actual number of evaluations may somewhat exceed MAXEVAL: MAXEVAL is rounded up to an integer number of subregion evaluations.<nowiki>]</nowiki> Otherwise, the integration stops when the estimated |error| is less than REQABSERROR (the absolute error requested) '''or''' when the |
| - | estimated |error| is less than REQRELERROR × |integral value| (the relative error requested). (Either of the error tolerances can be set to zero to ignore it.) | + | estimated |error| is less than REQRELERROR × |integral value| (the relative error requested). (Either of the error tolerances can be set to '''zero to ignore''' it.) |
| - | VAL and ERR are arrays of length FDIM, which upon return are the computed integral values and estimated errors, respectively. (The estimated errors are based on an embedded cubature rule of lower | + | For vector-valued integrands (FDIM > 1), NORM specifies the norm that is used to measure the error and determine convergence properties. |
| - | order; for smooth functions, this estimate is usually conservative.) | + | (The NORM argument is irrelevant for FDIM ≤ 1 and is ignored.) Given vectors ''v'' and ''e'' of estimated integrals and errors therein, respectively, the NORM argument takes on one of the following enumerated constant values: |
| - | The return value of adapt_integrate is 0 on success and nonzero if there was an error (currently, only out-of-memory situations). | + | * <code>ERROR_L1</code>, <code>ERROR_L2</code>, <code>ERROR_LINF</code>: the absolute error is measured as |''e''| and the relative error as |''e''|/|''v''|, where |...| is the [[w:Taxicab geometry|L<sub>1</sub>]], [[w:Euclidean distance|L<sub>2</sub>]], or [[w:Maximum norm|L<sub>∞</sub>]] [[w:Norm (mathematics)|norm]], respectively. (|''x''| in the L<sub>1</sub> norm is the sum of the absolute values of the components, in the L<sub>2</sub> norm is the root mean square of the components, and in the L<sub>∞</sub> norm is the maximum absolute value of the components) |
| - | The integrand function F should be a function of the form: | + | * <code>ERROR_INDIVIDUAL</code>: Convergence is achieved only when each integrand (each component of v and e) individually satisfies the requested error tolerances. |
| - | void f(unsigned ndim, const double *x, void *fdata, | + | * <code>ERROR_PAIRED</code>: Like <code>ERROR_INDIVIDUAL</code>, except that the integrands are grouped into consecutive pairs, with the error tolerance applied in an L2 sense to each pair. This option is mainly useful for integrating vectors of complex numbers, where each consecutive pair |
| - | unsigned fdim, double *fval); | + | of real integrands is the real and imaginary parts of a single complex integrand, and you only care about the error in the complex plane rather than the error in the real and imaginary parts separately. |
| - | Here, the input is an array X of length NDIM (the point to be evaluated), the output is an array FVAL of length FDIM (the vector of function values at the point X). | + | <code>VAL</code> and <code>ERR</code> are arrays of length <code>FDIM</code>, which upon return are the computed integral values and estimated errors, respectively. (The estimated errors are based on an embedded cubature rule of lower order; for smooth functions, this estimate is usually conservative.) |
| - | The FDATA argument of F is equal to the FDATA argument passed to <code>adapt_integrate</code>—this can be used by the caller to pass any additional information through to F as needed (rather than using global variables, which are not re-entrant). If F does not need any additional data, you can just pass FDATA = <code>NULL</code> and ignore the FDATA argument to F. | + | The return value of <code>hcubature</code> and <code>pcubature</code> is 0 on success and nonzero if there was an error (mainly only out-of-memory situations or if the integrand signals an error). For a nonzero return value, the contents of the <code>VAL</code> and <code>ERR</code> arrays are undefined. |
| + | |||
| + | The integrand function <code>F</code> should be a function of the form: | ||
| + | |||
| + | int f(unsigned ndim, const double *x, void *fdata, | ||
| + | unsigned fdim, double *fval); | ||
| + | |||
| + | Here, the input is an array <code>X</code> of length <code>NDIM</code> (the point to be evaluated), the output is an array <code>FVAL</code> of length <code>FDIM</code> (the vector of function values at the point <code>X</code>). he return value should be 0 on success or a nonzero value if an error occurred and the integration is to be terminated immediately (<code>hcubature</code> will then return a nonzero error code). | ||
| + | |||
| + | The <code>FDATA</code> argument of <code>F</code> is equal to the <code>FDATA</code> argument passed to <code>hcubature</code>—this can be used by the caller to pass any additional information through to <code>F</code> as needed (rather than using global variables, which are not re-entrant). If <code>F</code> does not need any additional data, you can just pass <code>FDATA</code> = <code>NULL</code> and ignore the <code>FDATA</code> argument to <code>F</code>. | ||
| === "Vectorized" interface === | === "Vectorized" interface === | ||
| - | These integration algorithms evaluate the integrand in "batches" of several points at a time. It is often useful to have access to this information so that your integrand function is not called for one point at a time, but rather for a whole "vector" of many points at once. For example, you may want to evaluate the integrand in parallel at different points. This functionality is available by calling: | + | These integration algorithms actually evaluate the integrand in "batches" of several points at a time. It is often useful to have access to this information so that your integrand function is not called for one point at a time, but rather for a whole "vector" of many points at once. For example, you may want to evaluate the integrand in parallel at different points. This functionality is available by calling: |
| + | |||
| + | int hcubature_v(unsigned fdim, integrand_v f, void *fdata, | ||
| + | unsigned dim, const double *xmin, const double *xmax, | ||
| + | unsigned maxEval, double reqAbsError, double reqRelError, | ||
| + | error_norm norm, double *val, double *err); | ||
| + | |||
| + | (and similarly for <code>pcubature_v</code>). All of the arguments and the return value are identical to <code>hcubature</code>, above, except that now the integrand <code>F</code> is of type <code>integrand_v</code>, corresponding to a function of a different form. The integrand function <code>F</code> should now be a function of the form: | ||
| + | |||
| + | int f(unsigned ndim, unsigned npts, const double *x, void *fdata, | ||
| + | unsigned fdim, double *fval); | ||
| - | int adapt_integrate_v(unsigned fdim, integrand_v f, void *fdata, | + | Now, <code>X</code> is not a single point, but an array of <code>NPTS</code> points (length <code>NPTS</code>×<code>NDIM</code>), and upon return the values of all <code>FDIM</code> integrands at all <code>NPTS</code> points should be stored in <code>FVAL</code> (length <code>NPTS</code>×<code>FDIM</code>). In particular, <code>x[i*ndim + j]</code> is the <code>j</code>-th coordinate of the <code>i</code>-th point (<code>i</code><<code>npts</code> and <code>j</code><<code>ndim</code>), and the <code>k</code>-th function evaluation (<code>k</code><<code>fdim</code>) for the <code>i</code>-th point is returned in <code>fval[i*fdim + k]</code>. ('''Note''': the <code>fval</code> indexing is changed compared to the <code>adapt_integrate_v</code> interface in previous versions.) |
| - | unsigned dim, const double *xmin, const double *xmax, | + | |
| - | unsigned maxEval, double reqAbsError, double reqRelError, | + | |
| - | double *val, double *err); | + | |
| - | All of the arguments and the return value are identical to <code>adapt_integrate</code>, above, except that now the integrand <code>F</code> is of type <code>integrand_v</code>, corresponding to a function of a different form. The integrand function F should now be a function of the form: | + | Again, the return value should be 0 on success or nonzero to terminate the integration immediately (e.g. if an error occurred). |
| - | void f(unsigned ndim, unsigned npts, const double *x, void *fdata, | + | The size of <code>NPTS</code> will vary with the dimensionality of the problem; higher-dimensional problems will have (exponentially) larger NPTS, allowing for the possibility of more parallelism. Currently, for <code>hcubature_v</code>, <code>NPTS</code> starts at 15 in 1d, 17 in 2d, and 33 in 3d, but as <code>adapt_integrate_v</code> calls your integrand more and more times the value of NPTS will grow. e.g. if you end up requiring several thousand points in total, <code>NPTS</code> may grow to several hundred. We utilize an algorithm from: |
| - | unsigned fdim, double *fval); | + | |
| - | Now, X is not a single point, but an array of NPTS points (length NPTS×NDIM), and upon return the values of all FDIM integrands at all NPTS points should be stored in FVAL (length FDIM×NPTS). In particular, <code>x[i*ndim + j]</code> is the <code>j</code>-th coordinate of the <code>i</code>-th point (<code>i</code><<code>npts</code> and <code>j</code><<code>ndim</code>), and the <code>k</code>-th function evaluation (<code>k</code><<code>fdim</code>) for the <code>i</code>-th point is returned in <code>fval[k*npt + i]</code>. | + | * I. Gladwell, "Vectorization of one dimensional quadrature codes," pp. 230–238 in ''Numerical Integration. Recent Developments, Software and Applications'', G. Fairweather and P. M. Keast, eds., NATO ASI Series C203, Dordrecht (1987). |
| - | The size of NPTS will vary with the dimensionality of the problem; higher-dimensional problems will have (exponentially) larger NPTS, allowing for the possibility of more parallelism. (However, for sufficiently high dimensions, e.g. >8, a different algorithm like Monte-Carlo integration or sparse grids is likely to be more efficient.) Currently, NPTS is 30 in 1d, 34 in 2d, and 66 in 3d, although the first call to <code>F</code> will have half that many points. | + | as described in the article "Parallel globally adaptive algorithms for multi-dimensional integration" by [http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.42.6638 Bull and Freeman] (1994). |
| === Example === | === Example === | ||
| Line 80: | Line 110: | ||
| #include "cubature.h" | #include "cubature.h" | ||
| - | void f(unsigned ndim, const double *x, void *fdata, unsigned fdim, double *fval) { | + | int f(unsigned ndim, const double *x, void *fdata, unsigned fdim, double *fval) { |
| double sigma = *((double *) fdata); ''// we can pass σ via fdata argument'' | double sigma = *((double *) fdata); ''// we can pass σ via fdata argument'' | ||
| double sum = 0; | double sum = 0; | ||
| Line 87: | Line 117: | ||
| ''// compute the output value: note that fdim should == 1 from below'' | ''// compute the output value: note that fdim should == 1 from below'' | ||
| fval[0] = exp(-sigma * sum); | fval[0] = exp(-sigma * sum); | ||
| + | return 0; ''// success'' | ||
| } | } | ||
| - | then, later in the program where we call <code>adapt_integrate</code>: | + | then, later in the program where we call <code>hcubature</code>: |
| { | { | ||
| double xmin[3] = {-2,-2,-2}, xmax[3] = {2,2,2}, sigma = 0.5, val, err; | double xmin[3] = {-2,-2,-2}, xmax[3] = {2,2,2}, sigma = 0.5, val, err; | ||
| - | adapt_integrate(1, f, &sigma, 3, xmin, xmax, 0, 0, 1e-4, &val, &err); | + | hcubature(1, f, &sigma, 3, xmin, xmax, 0, 0, 1e-4, ERROR_INDIVIDUAL, &val, &err); |
| printf("Computed integral = %0.10g +/- %g\n", val, err); | printf("Computed integral = %0.10g +/- %g\n", val, err); | ||
| } | } | ||
| Line 105: | Line 136: | ||
| Note that the estimated ''relative'' error is 0.00136919/13.69609043 = 9.9969×10<sup>–5</sup>, within our requested tolerance of <math>10^{-4}</math>. The ''actual'' error in the integral value, as can be determined e.g. by running the integration with a much lower tolerance, is much smaller: the integral is too small by about 0.00002, for an actual relative error of about 1.4×10<sup>–6</sup>. As mentioned above, for smooth integrands the estimated error is almost always conservative (which means, unfortunately, that the integrator usually does more function evaluations than it needs to). | Note that the estimated ''relative'' error is 0.00136919/13.69609043 = 9.9969×10<sup>–5</sup>, within our requested tolerance of <math>10^{-4}</math>. The ''actual'' error in the integral value, as can be determined e.g. by running the integration with a much lower tolerance, is much smaller: the integral is too small by about 0.00002, for an actual relative error of about 1.4×10<sup>–6</sup>. As mentioned above, for smooth integrands the estimated error is almost always conservative (which means, unfortunately, that the integrator usually does more function evaluations than it needs to). | ||
| - | With the vectorized interface <code>adapt_integrate_v</code>, one would instead do: | + | With the vectorized interface <code>hcubature_v</code>, one would instead use: |
| - | void f(unsigned ndim, unsigned npts, const double *x, void *fdata, unsigned fdim, double *fval) { | + | int f(unsigned ndim, unsigned npts, const double *x, void *fdata, unsigned fdim, double *fval) { |
| double sigma = *((double *) fdata); | double sigma = *((double *) fdata); | ||
| unsigned i, j; | unsigned i, j; | ||
| Line 115: | Line 146: | ||
| fval[j] = exp(-sigma * sum); | fval[j] = exp(-sigma * sum); | ||
| } | } | ||
| + | return 0; ''// success'' | ||
| } | } | ||
| Line 121: | Line 153: | ||
| Integrals over infinite or semi-infinite intervals is possible by a [[w:Integration by substitution|change of variables]]. This is best illustrated in one dimension. | Integrals over infinite or semi-infinite intervals is possible by a [[w:Integration by substitution|change of variables]]. This is best illustrated in one dimension. | ||
| - | To compute an integral over a semi-infinite interval, you can perform the change of variables ''x''=1/(1-''t''): | + | To compute an integral over a semi-infinite interval, you can perform the change of variables ''x''=a+''t''/(1-''t''): |
| - | :<math>\int_0^\infty f(x) dx = \int_0^1 f\left(\frac{1}{1-t}\right) \frac{1}{(1-t)^2} dt .</math> | + | :<math>\int_a^\infty f(x) dx = \int_0^1 f\left(a + \frac{t}{1-t}\right) \frac{1}{(1-t)^2} dt .</math> |
| For an infinite interval, you can perform the change of variables ''x''=''t''/(1-''t''<sup>2</sup>): | For an infinite interval, you can perform the change of variables ''x''=''t''/(1-''t''<sup>2</sup>): | ||
| :<math>\int_{-\infty}^\infty f(x) dx = \int_{-1}^1 f\left(\frac{t}{1-t^2}\right) \frac{1 + t^2}{(1-t^2)^2} dt .</math> | :<math>\int_{-\infty}^\infty f(x) dx = \int_{-1}^1 f\left(\frac{t}{1-t^2}\right) \frac{1 + t^2}{(1-t^2)^2} dt .</math> | ||
| - | Note the [[w:Jacobian matrix|Jacobian]] factors multiplying ''f''(⋅⋅⋅) in both integrals. | + | Note the [[w:Jacobian matrix|Jacobian]] factors multiplying ''f''(⋅⋅⋅) in both integrals, and also that the limits of the ''t'' integrals are different in the two cases. |
| In multiple dimensions, one simply performs this change of variables on each dimension separately, as desired, multiplying the integrand by the corresponding Jacobian factor for each dimension being transformed. | In multiple dimensions, one simply performs this change of variables on each dimension separately, as desired, multiplying the integrand by the corresponding Jacobian factor for each dimension being transformed. | ||
| - | The Jacobian factors diverge as the endpoints are approached. However, in order for your integral to have been finite in the first place it must be true that ''f''(''x'') goes to zero at infinity faster than 1/''x'', hence the limit of the integrand multiplied by the Jacobian is zero at the endpoints. In any case, the quadrature/cubature rules currently employed in <code>cubature.c</code> do not evaluate the integrand at the endpoints, so you need not implement special handling for |''t''|=1. | + | The Jacobian factors diverge as the endpoints are approached. However, if ''f''(''x'') goes to zero at least as fast as 1/''x''<sup>2</sup>, then the limit of the integrand (including the Jacobian factor) is finite at the endpoints. If your ''f''(''x'') vanishes more slowly than 1/''x''<sup>2</sup> but still faster than 1/''x'', then the integrand blows up at the endpoints but the integral is still finite (it is an integrable singularity), so the code will work (although it may take many function evaluations to converge). If your ''f''(''x'') vanishes only as 1/''x'', then it is not [[w:Absolute convergence|absolutely convergent]] and much more care is required even to define what you are trying to compute. (In any case, the h-adaptive quadrature/cubature rules currently employed in <code>cubature.c</code> do not evaluate the integrand at the endpoints, so you need not implement special handling for |''t''|=1.) |
| == Test program == | == Test program == | ||
| - | To compile a test program, just compile <code>cubature.c</code> while #defining <code>TEST_INTEGRATOR</code>, e.g. (on Unix or GNU/Linux) via: | + | To compile a test programs, just compile <code>hcubature.c</code> and/or <code>pcubature.c</code> along with the test program <code>test.c</code>, e.g. (on Unix or GNU/Linux) via: |
| - | cc -DTEST_INTEGRATOR -o cubature_test cubature.c -lm | + | cc -o htest test.c hcubature.c -l |
| + | cc -o ptest -DPCUBATURE test.c pcubature.c -lm | ||
| The usage is then: | The usage is then: | ||
| - | ./cubature_test <dim> <tol> <integrand> <maxeval> | + | ./htest <dim> <tol> <integrand> <maxeval> |
| - | where <dim> = # dimensions, <tol> = relative tolerance, <integrand> is 0–7 for one of eight possible test integrands (see below) and <maxeval> is the maximum number of function evaluations (0 for none, the default). | + | where <dim> = # dimensions, <tol> = relative tolerance, <integrand> is 0–7 for one of eight possible test integrands (see below) and <maxeval> is the maximum number of function evaluations (0 for none, the default). Similarly for <code>ptest</code> (which tests the <code>pcubature</code> function). |
| The different test integrands are: | The different test integrands are: | ||
| Line 156: | Line 189: | ||
| For example: | For example: | ||
| - | ./cubature_test 3 1e-5 4 | + | ./htest 3 1e-5 4 |
| integrates the Gaussian function (4) to a desired relative error tolerance of 10<sup>–5</sup> in 3 dimensions. The output is: | integrates the Gaussian function (4) to a desired relative error tolerance of 10<sup>–5</sup> in 3 dimensions. The output is: | ||
Current revision
Contents |
Cubature
Steven G. Johnson has written a simple C package for adaptive multidimensional integration (cubature) of vector-valued integrands over hypercubes, i.e. to compute integrals of the form:
(Of course, it can handle scalar integrands as the special case where 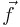 is a one-dimensional vector: the dimensionalities of
is a one-dimensional vector: the dimensionalities of 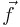 and
and 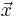 are independent.) The integrand can be evaluated for an array of points at once to enable easy parallelization. The code, which is distributed as free software under the terms of the GNU General Public License (v2 or later), implements two algorithms for adaptive integration.
are independent.) The integrand can be evaluated for an array of points at once to enable easy parallelization. The code, which is distributed as free software under the terms of the GNU General Public License (v2 or later), implements two algorithms for adaptive integration.
The first, h-adaptive integration (recursively partitioning the integration domain into smaller subdomains, applying the same integration rule to each, until convergence is achieved), is based on the algorithms described in:
- A. C. Genz and A. A. Malik, "An adaptive algorithm for numeric integration over an N-dimensional rectangular region," J. Comput. Appl. Math. 6 (4), 295–302 (1980).
- J. Berntsen, T. O. Espelid, and A. Genz, "An adaptive algorithm for the approximate calculation of multiple integrals," ACM Trans. Math. Soft. 17 (4), 437–451 (1991).
This algorithm is best suited for a moderate number of dimensions (say, < 7), and is superseded for high-dimensional integrals by other methods (e.g. Monte Carlo variants or sparse grids).
(Note that we do not use any of the original DCUHRE code by Genz, which is not under a free/open-source license.) Our code is based in part on code borrowed from the HIntLib numeric-integration library by Rudolf Schürer and from code for Gauss-Kronrod quadrature (for 1d integrals) from the GNU Scientific Library, both of which are free software under the GNU GPL. (Another free-software multi-dimensional integration library, unrelated to our code here but also implementing the Genz–Malik algorithm among other techniques, is Cuba.)
The second, p-adaptive integration (repeatedly doubling the degree of the quadrature rules until convergence is achieved), is based on a tensor product of Clenshaw–Curtis quadrature rules. This algorithm is often superior to h-adaptive integration for smooth integrands in a few (≤3) dimensions, but is a poor choice in higher dimensions or for non-smooth integrands.
For the most part, the p-adaptive routines below are drop-in replacements for the h-adaptive routines, with the same arguments etcetera, so you can experiment to see which one works best for your problem. One difference: the h-adaptive routines do *not* evaluate the integrand on the boundaries of the integration volume, whereas the p-adaptive routines *do* evaluate the integrand at the boundaries. This means that the p adaptive routines require more care in cases where there are singularities at the boundaries.
I am also grateful to Dmitry Turbiner (dturbiner ατ alum.mit.edu), who implemented an initial prototype of the "vectorized" functionality (see below) for evaluating an array of points in a single call, which facilitates parallelization of the integrand evaluation.
Download
The current version of the code can be downloaded from:
a gzipped tar file. This unpacks to a directory containing a README file with instructions and a stand-alone hcubature.c or pcubature.c file (along with a couple of private header files) that you can compile and link into your program for h-adaptive and p-adaptive integration, respectively, and a header file cubature.h that you #include.
The test.c file contains a little test program which is produced if you compile that file with -DHCUBATURE or -DPCUBATURE and link with hcubature.c or pcubature.c, respectively, as described below.
B. Narasimhan wrote a GNU R interface, which can be downloaded here: http://cran.r-project.org/web/packages/cubature/index.html.
A Julia interface can be obtained from Cubature.jl. A Python cubature.py interface written by Saullo Castro is also available.
Usage
You should compile hcubature.c and/or pcubature.c and link it with your program, and #include the header file cubature.h.
The central subroutine you will be calling for h-adaptive cubature is:
int hcubature(unsigned fdim, integrand f, void *fdata,
unsigned dim, const double *xmin, const double *xmax,
size_t maxEval, double reqAbsError, double reqRelError,
error_norm norm,
double *val, double *err);
or pcubature (same arguments) for p-adaptive cubature. (See also the vectorized interface below.)
This integrates a function F(x), returning a vector of FDIM integrands, where x is a DIM-dimensional vector ranging from XMIN to XMAX (i.e. in a hypercube XMINi ≤ xi ≤ XMAXi).
MAXEVAL specifies a maximum number of function evaluations (0 for no limit). [Note: the actual number of evaluations may somewhat exceed MAXEVAL: MAXEVAL is rounded up to an integer number of subregion evaluations.] Otherwise, the integration stops when the estimated |error| is less than REQABSERROR (the absolute error requested) or when the estimated |error| is less than REQRELERROR × |integral value| (the relative error requested). (Either of the error tolerances can be set to zero to ignore it.)
For vector-valued integrands (FDIM > 1), NORM specifies the norm that is used to measure the error and determine convergence properties. (The NORM argument is irrelevant for FDIM ≤ 1 and is ignored.) Given vectors v and e of estimated integrals and errors therein, respectively, the NORM argument takes on one of the following enumerated constant values:
-
ERROR_L1,ERROR_L2,ERROR_LINF: the absolute error is measured as |e| and the relative error as |e|/|v|, where |...| is the L1, L2, or L∞ norm, respectively. (|x| in the L1 norm is the sum of the absolute values of the components, in the L2 norm is the root mean square of the components, and in the L∞ norm is the maximum absolute value of the components)
-
ERROR_INDIVIDUAL: Convergence is achieved only when each integrand (each component of v and e) individually satisfies the requested error tolerances.
-
ERROR_PAIRED: LikeERROR_INDIVIDUAL, except that the integrands are grouped into consecutive pairs, with the error tolerance applied in an L2 sense to each pair. This option is mainly useful for integrating vectors of complex numbers, where each consecutive pair
of real integrands is the real and imaginary parts of a single complex integrand, and you only care about the error in the complex plane rather than the error in the real and imaginary parts separately.
VAL and ERR are arrays of length FDIM, which upon return are the computed integral values and estimated errors, respectively. (The estimated errors are based on an embedded cubature rule of lower order; for smooth functions, this estimate is usually conservative.)
The return value of hcubature and pcubature is 0 on success and nonzero if there was an error (mainly only out-of-memory situations or if the integrand signals an error). For a nonzero return value, the contents of the VAL and ERR arrays are undefined.
The integrand function F should be a function of the form:
int f(unsigned ndim, const double *x, void *fdata,
unsigned fdim, double *fval);
Here, the input is an array X of length NDIM (the point to be evaluated), the output is an array FVAL of length FDIM (the vector of function values at the point X). he return value should be 0 on success or a nonzero value if an error occurred and the integration is to be terminated immediately (hcubature will then return a nonzero error code).
The FDATA argument of F is equal to the FDATA argument passed to hcubature—this can be used by the caller to pass any additional information through to F as needed (rather than using global variables, which are not re-entrant). If F does not need any additional data, you can just pass FDATA = NULL and ignore the FDATA argument to F.
"Vectorized" interface
These integration algorithms actually evaluate the integrand in "batches" of several points at a time. It is often useful to have access to this information so that your integrand function is not called for one point at a time, but rather for a whole "vector" of many points at once. For example, you may want to evaluate the integrand in parallel at different points. This functionality is available by calling:
int hcubature_v(unsigned fdim, integrand_v f, void *fdata,
unsigned dim, const double *xmin, const double *xmax,
unsigned maxEval, double reqAbsError, double reqRelError,
error_norm norm, double *val, double *err);
(and similarly for pcubature_v). All of the arguments and the return value are identical to hcubature, above, except that now the integrand F is of type integrand_v, corresponding to a function of a different form. The integrand function F should now be a function of the form:
int f(unsigned ndim, unsigned npts, const double *x, void *fdata,
unsigned fdim, double *fval);
Now, X is not a single point, but an array of NPTS points (length NPTS×NDIM), and upon return the values of all FDIM integrands at all NPTS points should be stored in FVAL (length NPTS×FDIM). In particular, x[i*ndim + j] is the j-th coordinate of the i-th point (i<npts and j<ndim), and the k-th function evaluation (k<fdim) for the i-th point is returned in fval[i*fdim + k]. (Note: the fval indexing is changed compared to the adapt_integrate_v interface in previous versions.)
Again, the return value should be 0 on success or nonzero to terminate the integration immediately (e.g. if an error occurred).
The size of NPTS will vary with the dimensionality of the problem; higher-dimensional problems will have (exponentially) larger NPTS, allowing for the possibility of more parallelism. Currently, for hcubature_v, NPTS starts at 15 in 1d, 17 in 2d, and 33 in 3d, but as adapt_integrate_v calls your integrand more and more times the value of NPTS will grow. e.g. if you end up requiring several thousand points in total, NPTS may grow to several hundred. We utilize an algorithm from:
- I. Gladwell, "Vectorization of one dimensional quadrature codes," pp. 230–238 in Numerical Integration. Recent Developments, Software and Applications, G. Fairweather and P. M. Keast, eds., NATO ASI Series C203, Dordrecht (1987).
as described in the article "Parallel globally adaptive algorithms for multi-dimensional integration" by Bull and Freeman (1994).
Example
As a simple example, consider the Gaussian integral of the scalar function 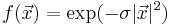 over the hypercube [ − 2,2]3 in 3 dimensions. You could compute this integral via code that looks like:
over the hypercube [ − 2,2]3 in 3 dimensions. You could compute this integral via code that looks like:
#include <stdio.h>
#include <math.h>
#include "cubature.h"
int f(unsigned ndim, const double *x, void *fdata, unsigned fdim, double *fval) {
double sigma = *((double *) fdata); // we can pass σ via fdata argument
double sum = 0;
unsigned i;
for (i = 0; i < ndim; ++i) sum += x[i] * x[i];
// compute the output value: note that fdim should == 1 from below
fval[0] = exp(-sigma * sum);
return 0; // success
}
then, later in the program where we call hcubature:
{
double xmin[3] = {-2,-2,-2}, xmax[3] = {2,2,2}, sigma = 0.5, val, err;
hcubature(1, f, &sigma, 3, xmin, xmax, 0, 0, 1e-4, ERROR_INDIVIDUAL, &val, &err);
printf("Computed integral = %0.10g +/- %g\n", val, err);
}
Here, we have specified a relative error tolerance of 10 − 4 (and no absolute error tolerance or maximum number of function evaluations). Note also that, to demonstrate the fdata parameter, we have used it to pass the σ value through to our function (rather than hard-coding the value of σ in f or using a global variable).
The output should be:
Computed integral = 13.69609043 +/- 0.00136919
Note that the estimated relative error is 0.00136919/13.69609043 = 9.9969×10–5, within our requested tolerance of 10 − 4. The actual error in the integral value, as can be determined e.g. by running the integration with a much lower tolerance, is much smaller: the integral is too small by about 0.00002, for an actual relative error of about 1.4×10–6. As mentioned above, for smooth integrands the estimated error is almost always conservative (which means, unfortunately, that the integrator usually does more function evaluations than it needs to).
With the vectorized interface hcubature_v, one would instead use:
int f(unsigned ndim, unsigned npts, const double *x, void *fdata, unsigned fdim, double *fval) {
double sigma = *((double *) fdata);
unsigned i, j;
for (j = 0; j < npts; ++j) { // evaluate the integrand for npts points
double sum = 0;
for (i = 0; i < ndim; ++i) sum += x[j*ndim+i] * x[j*ndim+i];
fval[j] = exp(-sigma * sum);
}
return 0; // success
}
Infinite intervals
Integrals over infinite or semi-infinite intervals is possible by a change of variables. This is best illustrated in one dimension.
To compute an integral over a semi-infinite interval, you can perform the change of variables x=a+t/(1-t):
For an infinite interval, you can perform the change of variables x=t/(1-t2):
Note the Jacobian factors multiplying f(⋅⋅⋅) in both integrals, and also that the limits of the t integrals are different in the two cases.
In multiple dimensions, one simply performs this change of variables on each dimension separately, as desired, multiplying the integrand by the corresponding Jacobian factor for each dimension being transformed.
The Jacobian factors diverge as the endpoints are approached. However, if f(x) goes to zero at least as fast as 1/x2, then the limit of the integrand (including the Jacobian factor) is finite at the endpoints. If your f(x) vanishes more slowly than 1/x2 but still faster than 1/x, then the integrand blows up at the endpoints but the integral is still finite (it is an integrable singularity), so the code will work (although it may take many function evaluations to converge). If your f(x) vanishes only as 1/x, then it is not absolutely convergent and much more care is required even to define what you are trying to compute. (In any case, the h-adaptive quadrature/cubature rules currently employed in cubature.c do not evaluate the integrand at the endpoints, so you need not implement special handling for |t|=1.)
Test program
To compile a test programs, just compile hcubature.c and/or pcubature.c along with the test program test.c, e.g. (on Unix or GNU/Linux) via:
cc -o htest test.c hcubature.c -l cc -o ptest -DPCUBATURE test.c pcubature.c -lm
The usage is then:
./htest <dim> <tol> <integrand> <maxeval>
where <dim> = # dimensions, <tol> = relative tolerance, <integrand> is 0–7 for one of eight possible test integrands (see below) and <maxeval> is the maximum number of function evaluations (0 for none, the default). Similarly for ptest (which tests the pcubature function).
The different test integrands are:
- 0: a product of cosine functions
- 1: a Gaussian integral of exp(-x^2), remapped to [0,infinity) limits
- 2: volume of a hypersphere (integrating a discontinuous function!)
- 3: a simple polynomial (product of coordinates)
- 4: a Gaussian centered in the middle of the integration volume
- 5: a sum of two Gaussians
- 6: an example function by Tsuda, a product of terms with near poles
- 7: a test integrand by Morokoff and Caflisch, a simple product of dim-th roots of the coordinates (weakly singular at the boundary)
For example:
./htest 3 1e-5 4
integrates the Gaussian function (4) to a desired relative error tolerance of 10–5 in 3 dimensions. The output is:
3-dim integral, tolerance = 1e-05 integrand 4: integral = 1, est err = 9.99952e-06, true err = 2.54397e-08 #evals = 82203
Notice that it finds the integral after 82203 function evaluations with an estimated error of about 10–5, but the true error (compared to the exact result) is much smaller (2.5×10–8): the error estimation is typically conservative when applied to smooth functions like this.