Casimir calculations in Meep

It is possible to use the Meep time-domain simulation code in order to calculate Casimir forces (and related quantities), a quantum-mechanical force that can arise even between neutral bodies due to quantum vacuum fluctuations in the electromagnetic field, or equivalently as a result of geometry dependence in the quantum vacuum energy.

Calculating Casimir forces in a classical time-domain Maxwell simulation like Meep is possible because of a new algorithm described in:

Alejandro W. Rodriguez, Alexander P. McCauley, John D. Joannopoulos, and Steven G. Johnson, "Casimir forces in the time domain: I. Theory," arXiv preprint archive article arXiv:0904.0267 (April 2009).
Alexander P. McCauley, Alejandro W. Rodriguez, John D. Joannopoulos, and Steven G. Johnson, "Casimir forces in the time domain: II. Applications," manuscript in preparation (2009).

This page will provide some tutorial examples showing how these calculations are performed for simple geometries.

Introduction

In this section, we introduce the equations and basic considerations involved in computing the force using the method presented in Rodriguez et. al. (arXiv:0904.0267). Note that we keep the details of the derivation to a minimum and instead focus on the calculational aspects of the resulting algorithm.

The basic steps involved in computing the Casimir force, as outlined in <ref name="Rodriguez"/>, are:

1. Map the problem onto a new problem with dissipation. Here, as in <ref name="Rodriguez"/>, we choose a frequency-independent conductivity $σ$ .

2. Measure the electric E and magnetic H fields in response to current pulses placed at each point along a surface enclosing the body of interest.

3. Integrate these fields in spave over the enclosing surface and then integrate this result, multiplied by a known function $g ( - t)$ , over time $t$ .

<ref>Note that the precise implementation of steps (1) and (2) will greatly affect the efficiency of the method. For example, computing the fields due to each source at each point on the surface separately requires a separate Meep calculation for each source (and polarization). As described in <ref name="Rodriguez"/>, and further below, it is possible to modify these steps in order to optimize the calculation of the stress tensor over the spatial surface. For the purpose of this introduction, however, we do not require specific details on how we handle the spatial integration.</ref>

The Casimir force on a body in the $i$ th direction is given by:

$F_i(t) = \textrm{Im} \, \frac{\hbar}{\pi} \sum_{n=0}^{T} g(-n\Delta t) \left[ \Gamma_i^E(n\Delta t) + \Gamma_i^H(n\Delta t) \right]$

where $Δ t$ denotes the temporal discretization inherent in any FDTD method (in meep, it is given by by $Δ t = S Δ x$ , as discussed in <ref>http://ab-initio.mit.edu/wiki/index.php/Meep_Introduction</ref>) and $T$ is a time cutoff which in the limit 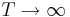$T \to \infty$ yields the exact force (in the limit of infinite resolution $\Delta t \to 0$ ) and which can often be chosen to be small due to the exponential decay in the functions $Γ i$ . The Kernel $g ( - n Δ t)$ is given by a DFT of a pre-determined function:

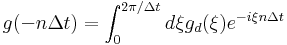
$g(-n \Delta t) = \int_{0}^{2\pi / \Delta t} d\xi g_d(\xi) e^{-i\xi n \Delta t}$

where,

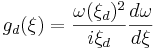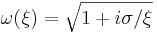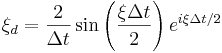$g_d(\xi) = \frac{\omega(\xi_d)^2}{i \xi_d} \frac{d\omega}{d\xi}$ , $\omega(\xi) = \sqrt{1 + i \sigma / \xi}$ and $\xi_d = \frac{2}{\Delta t} \sin \left(\frac{\xi \Delta t}{2}\right) e^{i \xi \Delta t / 2}$ .

Note that it is important to obtain $g ( - n Δ t)$ to good accuracy, but this is not a problem since the function need only be computed once for a given $σ$ and $Δ t$ . The 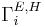$\Gamma_i^{E,H}$ are given by:

$\Gamma^E_i(n \Delta t) = \oint_{\vec{r} \in S} \sum_{j} \varepsilon(\vec{r}) \left[E_{i,j}(\vec{r},n \Delta t) - \frac{1}{2} \delta_{ij} E_{k,k}(\vec{r}, n \Delta t) \right]$

$\Gamma^H_i(n \Delta t) = \oint_{\vec{r} \in S} \sum_{j} \varepsilon(\vec{r}) \left[H_{i,j}(\vec{r},n \Delta t) - \frac{1}{2} \delta_{ij} H_{k,k}(\vec{r}, n \Delta t) \right]$ ,

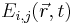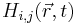where $E_{i,j}(\vec{r},t)$ and $H_{i,j}(\vec{r},t)$ are the electric and magnetic responses due to current sources placed along the surface of the body $S$ , and can be obtained as the output of a Meep calculation in a system with conductivity $σ D$ and $σ H$ , respectively (see <ref>http://ab-initio.mit.edu/wiki/index.php/Meep_Introduction</ref>).

Computing $Γ$ (t)

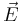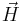The only quantity above that requires Meep are the $Γ i$ functions, which are determined by the spatial integration of the $\vec{E}$ - and $\vec{H}$ -field response to a dipole current source. There are two ways to obtain $Γ i$ , briefly explained below.

A. Each source separately:

To obtain 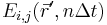$E_{i,j}(\vec{r}',n\Delta t)$ at some 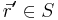$\vec{r}' \in S$ , one simply places a dipole current source 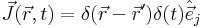$\vec{J}(\vec{r},t) = \delta(\vec{r}-\vec{r}') \delta(t) \hat{\vec{e}}_j$ (in the $j$ th direction) and finds the electric 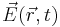$\vec{E}(\vec{r},t)$ response (at the same point 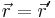$\vec{r}=\vec{r}'$ ) in the presence of an electric conductivity (a non-zero $σ D$ in Meep). 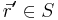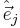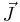This calculation is then repeated for all $\vec{r}' \in S$ and all three polarizations $\hat{\vec{e}}_j$ of $\vec{J}$ , and can be performed in parallel, since each source is independent from one another. The same holds for the calculation of $H i, j$ except that in this case one employs magnetic currents 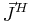$\vec{J}^H$ and conductivities $σ H$ .

B. Multipole expansion:

Coming soon.

Note that the surface of integration $S$ need not have any particular shape. In practice (2d and 3d), we often implement a simple square box (cube) enclosing the body of interest, for which the normals $d S j$ are easy to define (except at the corners, where they become ambiguous to define---due to the finite discretization, this is not a big concern, as seen from the example to follow).

Parallel plates

Coming soon.

2D geometry: square within square

To do.

Retrieved from "http://ab-initio.mit.edu/wiki/index.php/Casimir_calculations_in_Meep"

Category: Meep

 ==Introduction==
-In this section, we introduce the equations and basic considerations involved in computing the force using the method presented in
+In this section, we introduce the equations and basic considerations involved in computing the force using the method presented in Rodriguez et. al. ([http://arxiv.org/abs/arXiv:0904.0267 arXiv:0904.0267]). Note that we keep the details of the derivation to a minimum and instead focus on the calculational aspects of the resulting algorithm.
-<ref name="Rodriguez">Rodriguez et. al. arXiv:0904.0267</ref>. Note that we keep the details of the derivation to a minimum and instead focus on the calculational aspects of the resulting algorithm.
 The basic steps involved in computing the Casimir force, as outlined in <ref name="Rodriguez"/>, are:

Casimir calculations in Meep

From AbInitio

Revision as of 18:48, 7 April 2009

Contents